剑指Offer_#51_数组中的逆序对

剑指Offer_#51_数组中的逆序对

剑指offer

Contents

• • 题目
  • 思路分析
  • 解答
    • 更加精简的代码

题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

思路分析

最直接的思路是暴力循环，即用两层循环循环判断每一对数字是否是逆序对，然后计数，时间复杂度为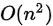,会超时。
所以必须时间复杂度更低的算法，这里用到了归并排序中的merge方法（详见算法第四版2.2节），只需要在标准的merge方法中添加一行计数的代码，即可实现本题的需求。

解答

class Solution {
    public int reversePairs(int[] nums) {
        int len = nums.length;
        if(len < 2) return 0;
        int[] copy = new int[len];
        //如果面试题不允许修改原数组nums,就需要拷贝原数组
        for(int i = 0;i <= len - 1;i++){
            copy[i] = nums[i];
        }
        int[] temp = new int[len];
        return reversePairs(copy, 0, len - 1, temp);
    }

    //递归函数
    private int reversePairs(int[] nums,int left,int right,int temp[]){
        //出口条件：给出的[left...right]区间内只有一个元素，逆序对是0
        if(left == right) return 0;
        //递推过程：分别计算当前区间左半段的逆序对，右半段的逆序对，跨越左右半段的逆序对，然后相加
        //防止出现大数溢出
        int mid = left + (right - left) / 2;
        //计算[left...mid]区间内的逆序对
        int leftPairs = reversePairs(nums, left, mid, temp);
        //计算[mid+1...right]区间内的逆序对
        int rightPairs = reversePairs(nums, mid + 1, right, temp);
        //如果整个数组都是有序的，那么不需要继续进行归并了
        if(nums[mid] <= nums[mid+1]) return leftPairs + rightPairs;
        //归并两个有序的区间，然后计算这跨越两个区间的逆序对数目
        int crossPairs = mergeAndCount(nums, left, mid, right, temp);
        return leftPairs + rightPairs + crossPairs;
    }

    private int mergeAndCount(int[] nums, int left, int mid,int right,int[] temp){
        //复制nums到temp
        for(int i = left;i <= right;i++){
            temp[i] = nums[i];
        }
        int i = left;
        int j = mid + 1;
        int count = 0;
        //归并[left...mid]和[mid+1,right]两个有序数组，使得[left...right]范围内的数字为有序
        for(int k = left;k <= right;k++){
            //i指针越界，直接归并j指向的元素
            if(i == mid + 1){
                nums[k] = temp[j];
                j++;
            //j指针越界，直接归并i指向的元素
            }else if(j == right + 1){
                nums[k] = temp[i];
                i++;
            //这里不能写<，否则连相等的数字对也会计算在内
            }else if(temp[i] <= temp[j]){
                nums[k] = temp[i];
                i++;
            }else{
                nums[k] = temp[j];
                j++;
                //相比归并排序中的merge()方法，仅仅增加了这一行代码
                count += (mid - i + 1);
            }
        }
        return count;
    }
}

更加精简的代码

class Solution {
    int[] tmp;
    public int reversePairs(int[] nums) {
        //tmp作为归并排序的辅助数组
        tmp = new int[nums.length];
        return mergeAndCount(nums, 0, nums.length - 1);
    }
    
    private int mergeAndCount(int[] nums, int left, int right){
        if(left >= right) return 0;
        int mid = left + (right - left) / 2;
        //首先，需要分别对[left...mid],[mid+1, right]两个区间内部进行排序，并且计算出这两个区间内部的逆序对个数
        int res = mergeAndCount(nums, left, mid) + mergeAndCount(nums, mid + 1, right);
        //合并[left...mid],[mid...right]两个有序区间,并且计数两个区间之间的逆序对
        for(int i = left; i <= right; i++) tmp[i] = nums[i];
        int i = left, j = mid + 1;
        int count = 0;
        for(int k = left; k <= right; k++){
            //ERROR:注意这里的四个条件，不能同时运行，必须写成else if
            if(i == mid + 1){
                nums[k] = tmp[j];
                //ERROR:这里不要忘了后移指针
                j++;
            }
            else if(j == right + 1){
                nums[k] = tmp[i];
                i++;
            }
            else if(tmp[i] <= tmp[j]){
                nums[k] = tmp[i];
                i++;
            }else{
                nums[k] = tmp[j];
                j++;
                count += (mid - i + 1);
            }
        }
        return res + count;
    }
}