单变量线性回归（一）

使用TensorFlow进行算法设计与训练的核心步骤：（1）准备数据 （2）构建模型 （3）模型训练 （4）进行预测

单变量线性方程可以表示为： y = w * x + b

项目：通过生成人工数据集，随机生成一个近似采样随机分布，使得w=2.0， b=1， 并加入一个噪声，噪声的最大振幅为0.4（文末附完整代码）

第一步 生成人工数据集

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(5)
x_data = np.linspace(-1, 1, 100)
y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4
plt.scatter(x_data, y_data)
plt.plot(x_data, 2 * x_data + 1.0, color = 'red', linewidth = 3)
plt.show()

 

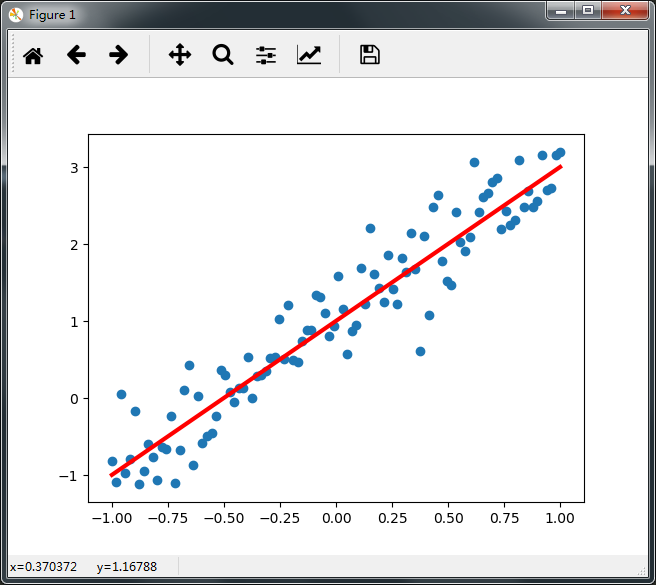
第二步 构建模型

2.1定义训练数据的占位符，x是特征值，y是标签值

x=tf.placeholder("float",name="x")
y =tf.placeholder("float",name="y")

2.2定义模型函数

def model(x,w,b):
    return tf.multiply(x,w)+ b

2.3定义模型结构

模型需要几个参数就定义几个变量，本项目需要定义两个变量。

• Tensorflow变量的声明函数是tf.Variable
• tf.Variable的作用是保存和更新参数
• 变量的初始值可以是随机数、常数，或是通过其他变量的初始值计算得到

第三步 训练模型

3.1设置训练参数

train epochs =10 #迭代次数(训练轮数) 

learning rate=0.05 #学习率，设置为经验值。

3.2定义损失函数

损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向，常见损失函数:均方差( MSE)和交叉熵( cross- entropy)

loss_function = tf.reduce_mean(tf.square(y-pred))  #采用均方差作为损失函数 

 3.3定义优化器

定义优化器 Optimizer,初始化一个 GradientDescentOptimizer  设置学习率和优化目标：最小化损失

optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)                #梯度下降优化器    

第四步 创建会话

sess = tf.Session()    #声明会话

init = tf.global_variables_initializer()   #初始化所有变量
sess.run(init)

第五步 迭代训练

模型训练阶段，设置迭代次数，每次通过将样本逐个输入模型，进行梯度下降优化操作，每次迭代后，绘制出模型曲线。

for epoch in range(train_epochs):  #采用SGD随机梯度下降优化方法
    for xs,ys in zip(x_data, y_data):     #zip()函数将x_data和y_data拼装在一起        每轮训练100次
        _, loss=sess.run([optimizer,loss_function], feed_dict={x: xs, y: ys})
    b0temp=b.eval(session=sess)
    w0temp=w.eval(session=sess)
    plt.plot(x_data, w0temp * x_data + b0temp)

plt.show()

运行结果如下：

 Note：本案例拟合的模型简单，训练3次之后已经接近收敛，虽然图中仅有3条直线，其实是有10条的，后面的都重合的。

5.1打印结果

print('w:', sess.run(w))   #w的值应在2附近
print('b:', sess.run(b))    #b的值应在1附近

#输出为 w = 1.9823 ； b = 1.04201

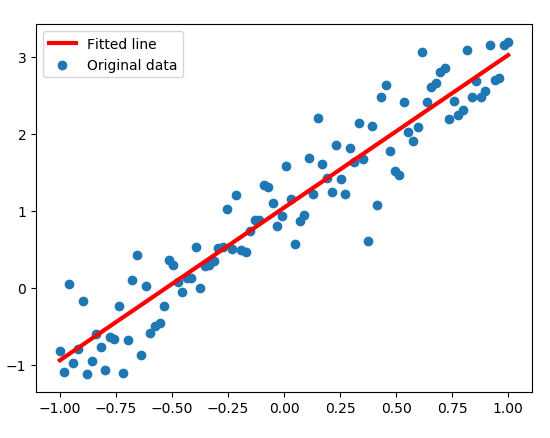
5.2可视化

plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, x_data * sess.run(w) + sess.run(b), label='Fitted line', color='r', linewidth=3)
plt.legend(loc=2)   #通过参数loc指定图例位置

plt.show()

第六步 进行预测

x_test = 3.21
predict = sess.run(pred, feed_dict={x:x_test})    # 方式一

#predict = sess.run(w) * x_test + sess.run(b)       方式二

print("预测值：%f" % predict)
target =2 * x_test +1.0
print("目标值：%f" % target)

输出结果为：

预测值：7.405184
目标值：7.420000

以上是利用Tensorflow训练一个线性模型并进行预测的完整过程，通过逐渐降低损失值loss来训练参数w和b拟合y=2x+1中的系数2和1，代码为：

#单变量线性回归项目：通过生成人工数据集，随机生成一个近似采样随机分布，使得w=2.0， b=1， 并加入一个噪声，噪声的最大振幅为0.4
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(5)
x_data = np.linspace(-1, 1, 100)
y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4
# plt.scatter(x_data, y_data)
# plt.plot(x_data, 2 * x_data + 1.0, color = 'red', linewidth = 3)
# plt.show()
x = tf.placeholder('float', name = 'x')
y = tf.placeholder('float', name = 'y')

def model(x, w, b):
    return  tf.multiply(x, w) + b

w = tf.Variable(1.0, name='w0')
b = tf.Variable(0.0 , name='b0')

pred = model(x, w, b)

train_epochs = 10  #迭代次数(训练轮数)
learning_rate = 0.05  #学习率，设置为经验值。

loss_function = tf.reduce_mean(tf.square(y - pred))  #采用均方差作为损失函数
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)  #梯度下降优化器

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

#采用SGD随机梯度下降优化方法
for epoch in range(train_epochs):
    for xs,ys in zip(x_data, y_data):
        _, loss=sess.run([optimizer,loss_function], feed_dict={x: xs, y: ys})
    b0temp=b.eval(session=sess)
    w0temp=w.eval(session=sess)
    # plt.plot(x_data, w0temp * x_data + b0temp)

# plt.show()
print('w:', sess.run(w))   #w的值应在2附近
print('b:', sess.run(b))   #b的值应在1附近

plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, x_data * sess.run(w) + sess.run(b), label='Fitted line', color='r', linewidth=3)
plt.legend(loc=2)  #通过参数loc指定图例位置
# plt.show()

#进行预测
x_test = 3.21
# predict = sess.run(pred, feed_dict={x:x_test})
predict = sess.run(w) * x_test + sess.run(b)
print("预测值：%f" % predict)

target =2 * x_test +1.0
print("目标值：%f" % target)

总结：

本文通过一个简单的例子介绍了利用Tensorflow实现机器学习的思路，重点讲解了下述步骤：
（1）生成人工数据集及其可视化
（2）构建线性模型
（3）定义损失函数
（4）定义优化器、最小化损失函数
（5）训练结果的可视化
（6）利用学习到的模型进行预测

 本案例的进阶内容（如显示损失值等）请看单变量线性回归（二）~~