11 分类与监督学习，朴素贝叶斯分类算法

1.理解分类与监督学习、聚类与无监督学习。

(1)简述分类与聚类的联系与区别。

①聚类分析是研究如何在没有训练的条件下把样本划分为若干类。聚类需要解决的问题是将已给定的若干无标记的模式聚集起来使之成为有意义的聚类。

②分类中，对于目标数据库中存在类别是已经清楚知道的，要做的是把某个对象划分到某个具体的已经定义的类别当中。

区别：分类是对类别进行实现的定义 ，最终类别数不变 。分类适合类别或分类体系已经确定的场合，比如按照国图分类法分类图书；

聚类则没有事先预定的类别，类别数不确定。 聚类不需要人工标注和预先训练分类器，类别在聚类过程中自动生成 。聚类则适合不存在分类体系、类别数不确定的场合，一般作为某些应用的前端，比如多文档文摘、搜索引擎结果后聚类(元搜索)等。

(2)简述什么是监督学习与无监督学习。

①监督学习：通过已有的训练样本（即已知数据以及其对应的输出）来训练，从而得到一个最优模型，再利用这个模型将所有新的数据样本映射为相应的输出结果，对输出结果进行简单的判断从而实现分类的目的，那么这个最优模型也就具有了对未知数据进行分类的能力。监督学习的典型例子就是决策树、神经网络以及疾病监测

②无监督学习：事先没有任何训练数据样本，需要直接对数据进行建模。而无监督学习就是很早之前的西洋双陆棋和聚类。

2.朴素贝叶斯分类算法 实例

　　利用关于心脏病患者的临床历史数据集，建立朴素贝叶斯心脏病分类模型。有六个分类变量(分类因子)：性别，年龄、KILLP评分、饮酒、吸烟、住院天数；目标分类变量疾病：心梗、不稳定性心绞痛

　　新的实例：–(性别=‘男’，年龄<70, KILLP=‘I'，饮酒=‘是’，吸烟≈‘是”，住院天数<7)；最可能是哪个疾病？上传手工演算过程。

	性别	年龄	KILLP	饮酒	吸烟	住院天数	疾病
1	男	>80	1	是	是	7-14	心梗
2	女	70-80	2	否	是	<7	心梗
3	女	70-81	1	否	否	<7	不稳定性心绞痛
4	女	<70	1	否	是	>14	心梗
5	男	70-80	2	是	是	7-14	心梗
6	女	>80	2	否	否	7-14	心梗
7	男	70-80	1	否	否	7-14	心梗
8	女	70-80	2	否	否	7-14	心梗
9	女	70-80	1	否	否	<7	心梗
10	男	<70	1	否	否	7-14	心梗
11	女	>80	3	否	是	<7	心梗
12	女	70-80	1	否	是	7-14	心梗
13	女	>80	3	否	是	7-14	不稳定性心绞痛
14	男	70-80	3	是	是	>14	不稳定性心绞痛
15	女	<70	3	否	否	<7	心梗
16	男	70-80	1	否	否	>14	心梗
17	男	<70	1	是	是	7-14	心梗
18	女	70-80	1	否	否	>14	心梗
19	男	70-80	2	否	否	7-14	心梗
20	女	<70	3	否	否	<7	不稳定性心绞痛

 

                    

3.使用朴素贝叶斯模型对iris数据集进行花分类。

尝试使用3种不同类型的朴素贝叶斯：

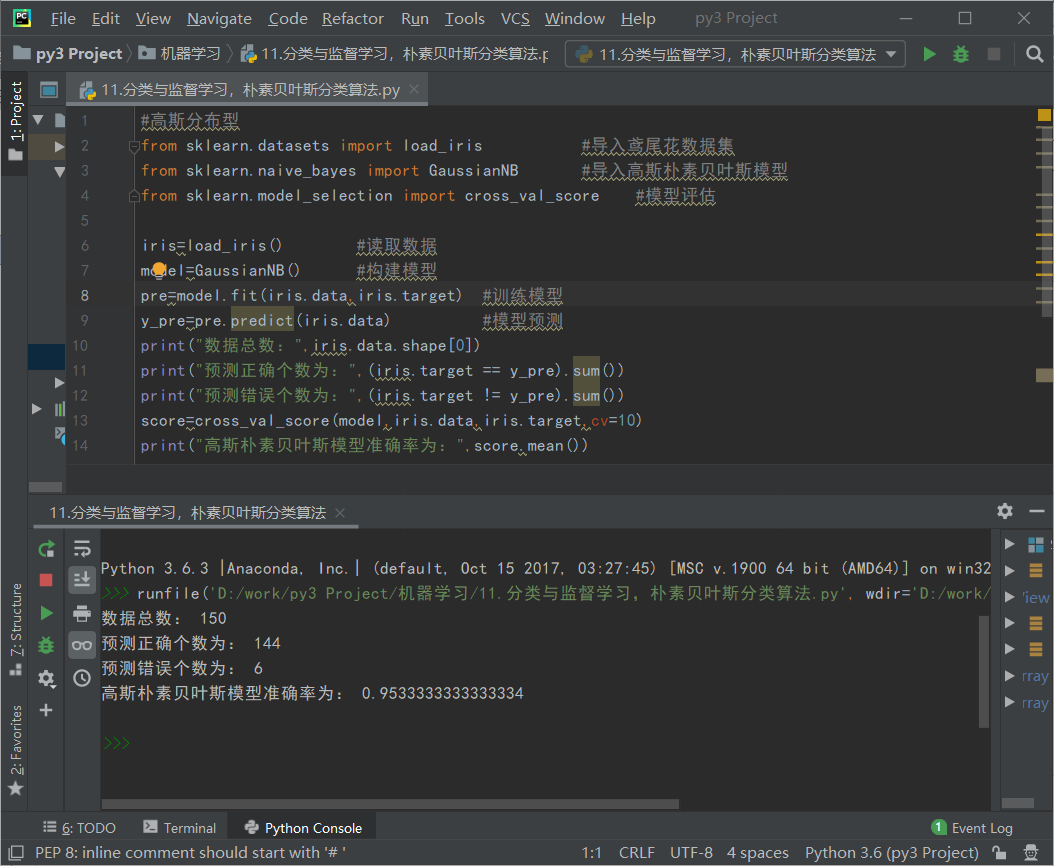
·高斯分布型

#高斯分布型
from sklearn.datasets import load_iris           #导入鸢尾花数据集
from sklearn.naive_bayes import GaussianNB       #导入高斯朴素贝叶斯模型
from sklearn.model_selection import cross_val_score    #模型评估

iris=load_iris()        #读取数据
model=GaussianNB()      #构建模型
pre=model.fit(iris.data,iris.target)  #训练模型
y_pre=pre.predict(iris.data)          #模型预测
print("数据总数：",iris.data.shape[0])
print("预测正确个数为：",(iris.target == y_pre).sum())
print("预测错误个数为：",(iris.target != y_pre).sum())
score=cross_val_score(model,iris.data,iris.target,cv=10)     #交叉验证
print("高斯朴素贝叶斯模型准确率为：",score.mean())

 

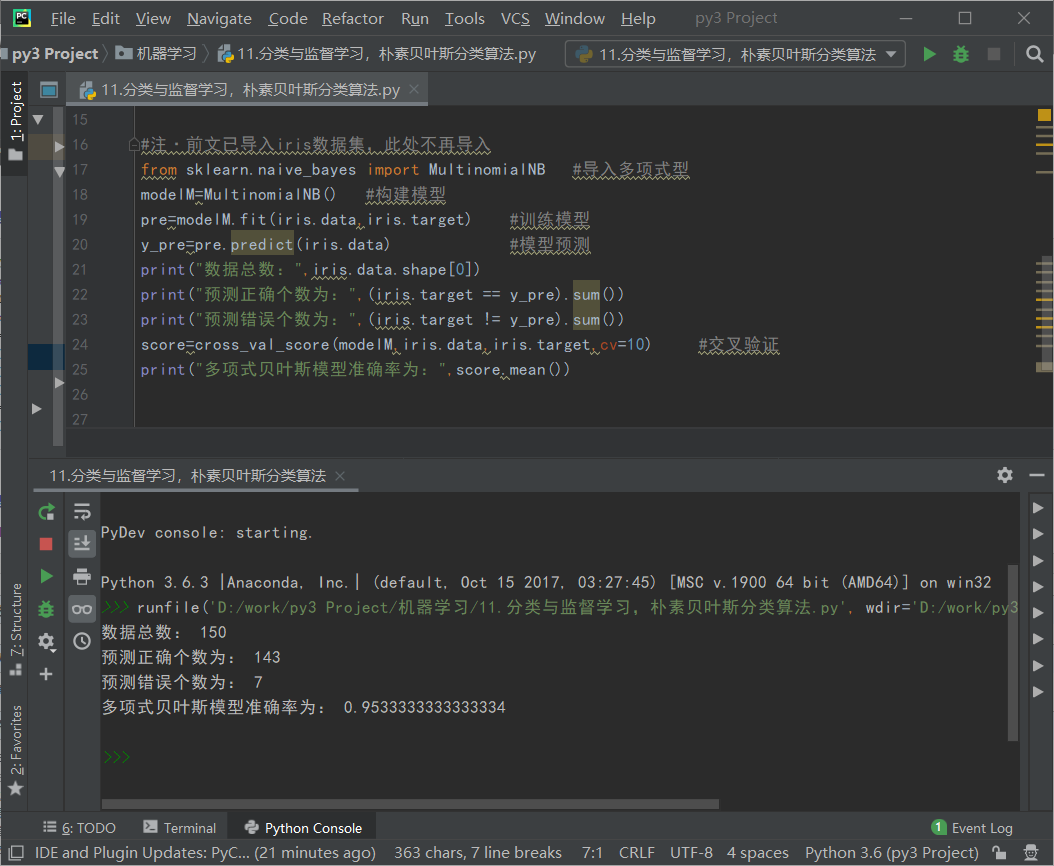
·多项式型

#注·前文已导入iris数据集，此处不再导入
from sklearn.naive_bayes import MultinomialNB   #导入多项式型
modelM=MultinomialNB()   #构建模型
pre=modelM.fit(iris.data,iris.target)    #训练模型
y_pre=pre.predict(iris.data)             #模型预测
print("数据总数：",iris.data.shape[0])
print("预测正确个数为：",(iris.target == y_pre).sum())
print("预测错误个数为：",(iris.target != y_pre).sum())
score=cross_val_score(modelM,iris.data,iris.target,cv=10)     #交叉验证
print("多项式贝叶斯模型准确率为：",score.mean())

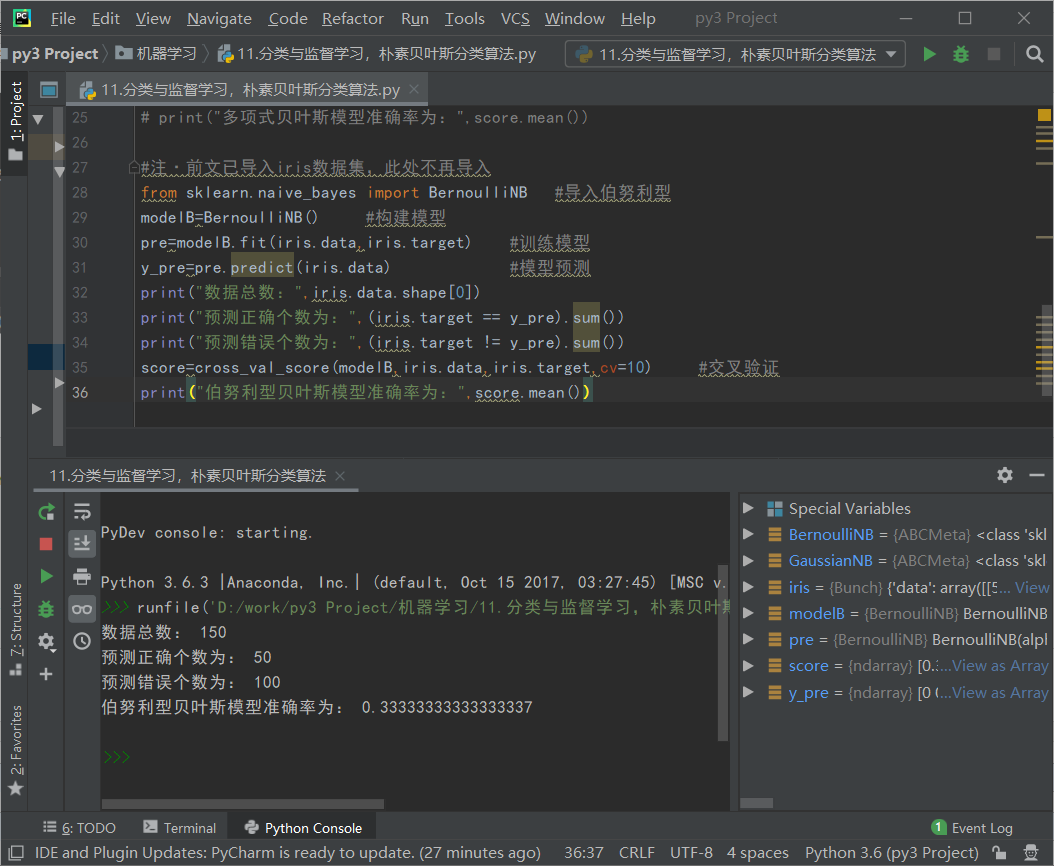
·伯努利型

#注·前文已导入iris数据集，此处不再导入
from sklearn.naive_bayes import BernoulliNB   #导入伯努利型
modelB=BernoulliNB()     #构建模型
pre=modelB.fit(iris.data,iris.target)    #训练模型
y_pre=pre.predict(iris.data)             #模型预测
print("数据总数：",iris.data.shape[0])
print("预测正确个数为：",(iris.target == y_pre).sum())
print("预测错误个数为：",(iris.target != y_pre).sum())
score=cross_val_score(modelB,iris.data,iris.target,cv=10)     #交叉验证
print("伯努利型贝叶斯模型准确率为：",score.mean())