并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。(百度百科)
解决并查集问题需要用到一种简单的数据结构——树:
每个节点有零个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树。(百度百科)
注意:如果只有一个树只有一个节点,那么它本身就是自己的父节点。
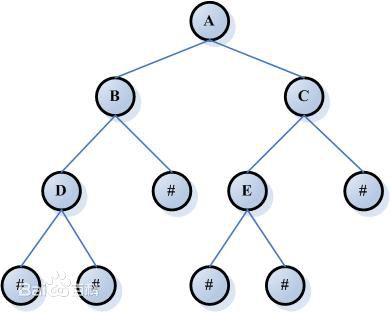
比如A的父节点是A,也是这个树的根节点,并且也是B和C的父节点;B和C是A的子节点。
解决并查集问题分为三步:(1)初始化 (2)查询 (3)合并
(1)初始化
我们准备n个节点保存n个元素,编号1-n。最开始每个元素相护独立,没有任何联系,表现为n个孤立的节点。

初始化代码:
void Input(int N){
for(int i = 0; i <= N; i++){
F[i] = i;
}
}
(2)查询
查询的目的是为了检查两个节点是否属于一个组,我们沿着树向上走,如果可以走到同一个根节点,那么我们就认为这两个元素属于同一个组。相当于每个树的根节点就是这个树独一无二的特点,可以看到(找到)这个特点,它两就是一家人。
查询代码:
int Find(int x){
return F[x] == x ? x : Find(F[x]);//先判断自己的根节点是不是自己,是返回x,不是继续查询父节点
}
但是这样效率比较低,在数据比较多,数字比较大时,可能会超时,那么我们可以把每个查询过的子节点和其根节点相连,构成只有两层的树结构,当再次查询是效率就会提升。可以进行路径压缩:
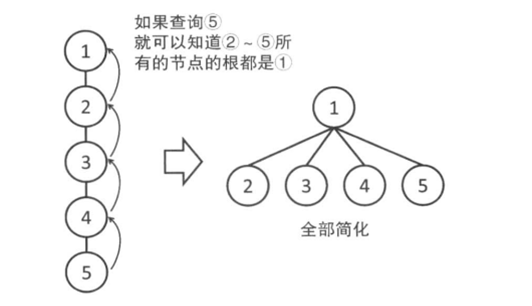
路径压缩后代码如下:
int Find(int x){ return F[x] == x ? x : F[x] = Find(F[x]);/*先判断自己的根节点是不是自己,是返回x,不是便把它的父节点设为根节点*/
}
(3)合并
若个查询到两个元素不是同一个组织,可以把它们进行合并。我们可以把其中甲方设置成为乙方的父节点便可,即其中甲方组织归属了乙方,它们的根节点相同。
代码如下:
void Union(int x, int y){
int Fx = Find(x);
int Fy = Find(y);
if(Fx != Fy){ //判断连个元素是否属于一个树,若不是便把Fx设置成为Fy的父节点
F[Fy] = Fx;
}
}