复位电路

　　时钟电路我第一篇博客已经说讲过了，今天我们来聊聊复位电路。当然，复位电路博大精深，并不是三言两语就能说清楚的，因此这里也是聊聊复位电路的基础，更深的研究需要在实际的项目中才能深有体会。本文的主要内容有:

　　　　·复位电路概述

　　　　·同步复位电路

　　　　·异步复位电路

　　　　·复位策略——复位网络

1.复位电路概述

　　复位信号在数字电路里面的重要性仅次于时钟信号。对电路的复位往往是指对触发器的复位，也就是说电路的复位中的这个“电路”，往往是指触发器，这是需要注意的。有的电路需要复位信号，就像是有的电路需要时钟信号那样，而有的电路是不需要复位信号的。复位又分为同步复位和异步复位，这两种各有优缺点。下面我们主要来说说复位信号的用途和不需要复位信号的情况。

(1)复位的目的

　　复位最基本的目的就是使电路(主要是触发器)进入一个能稳定操作的确定状态(主要是触发器在在某个确定的状态)，主要表现为下面两点:

①使电路在复位后从确定的初始状态运行:

　　·上电的时候，为了避免上电后进入随机状态而使电路紊乱，这个时候你就需要上电复位了。

　　·有时候，电路在某个状态下，你想或者别人要求你从电路的初始状态开始进行延时你的电路功能，这个时候你就要对你的电路进行复位，让它从最初的状态开始运行。

②使电路从错误状态回到可以控制的确定状态：

　　有的时候，你的电路发生了异常，比如说状态机跑飞了、系统供电炸了之类的，总之就是电路运行得不正常了，这个时候你就要对电路进行复位，让它从错误的状态回到一个正常的状态。

上面说的都是和实际电路有关的，下面我们就从电路仿真的角度看一下复位信号的重要性。

  ·仿真的要求

　　复位信号在仿真里面主要是使电路仿真时具有可知的初始值:

　　在仿真的时候，信号在初始状态是未知状态(也就是所谓的x，不过对信号初始化之后的这种情况除外，因为仿真的时候对信号初始化就使信号有了初始值，这就不是x了)。

  对于数据通路(数字系统一般分为数据通路和控制通路，数据通路一般是对输入的数据进行处理，控制通路则是对运行的情况进行操作)，在实际电路中，只要输入是有效数据(开始的时候可能不是有效的)，输出后的状态也是确定的;在仿真的时候，也是输入数据有效了，输出也就确定了。也就是说，初始不定态对数据通路的影响不明显。

  对于控制通路，在实际电路中，只要控制通路完备(比如说控制通路的状态机是完备的)，即使初始状态即使是不定态，在经过一定的循环后，还是能回到正确的状态上;然而在仿真的时候就不行了，仿真的时候由于初始状态为未知态，控制电路一开始就陷入了未知态;仿真跟实际电路不同，仿真是“串行”的，仿真时控制信号的初始不定态会导致后续的控制信号结果都是不定态，也就是说，初始的不定态对控制通道是致命的。

 

(2)不需要复位信号的一些情况

　　复位信号很重要，但是并不是每一部分的电路都需要复位电路，一方面是复位电路也消耗逻辑资源、占用芯片面积，另一方面是复位信号会增加电路设计的复杂性(比如要考虑复位的策略、复位的布局布线等等)。

  当某个电路的输出在任何时刻都可以不受到复位信号的控制就有正确的值时，比如说数据通路中的对数据进行处理的部分。在某些情况下，当流水线的寄存器(移位寄存触发器)在高速应用中时，应该去掉某些寄存器的复位信号以使设计达到更高的性能，因为带复位的触发器比不带复位的触发器更复杂，反应也更慢。

对复位信号/电路有一定的概念后，下面我们就来说说复位的方式，也就是同步电路和异步电路以及它们的优缺点。

 

2.同步复位

(1)同步复位电路

同步复位是指复位信号在时钟有效沿到来时才复位电路(主要是复位触发器)。因此同步复位的复位信号受到时钟信号的控制。同步复位的触发器RTL代码和电路如下所示:

 　　　　

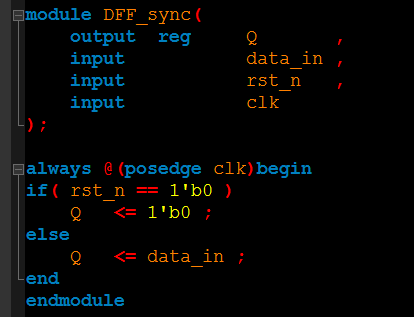
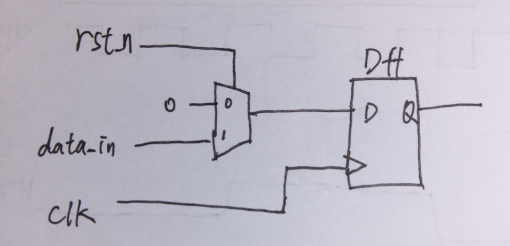
上面的电路在FPGA中容易综合得到；也有可能综合得到下面这样的电路：

　　　　　　　　　　　　　　　　　　　　　　

(2)同步复位的优点

　　①首先同步复位一般能确保电路是100%同步的，因为电路都是由同步时钟触发。

　　②同步复位会综合为更小的触发器（？？？更小？？感觉有点不太对，可能FPGA跟ASIC不一样吧？）。从前面电路中我们也可以看到，复位电路仅仅是由一个普通的触发器和一个与门够吃。

　　③由于同步复位仅仅发生在时钟的有效沿，当外部的复位信号由毛刺时，时钟可以当做过滤毛刺的手段，也就是说同步复位受到复位信号的毛刺影响小。

　　④当复位信号是由内部电路产生时，此时复位信号就有可能有毛刺，时钟就可以过滤毛刺。也就是说，可以在那些使用内部信号当做复位信号的设计中，使用同步复位。

 

(3)同步复位的缺点

　　①使用同步复位可能使综合工具无法分辨分辨复位信号和其他控制信号，导致进行复位的控制逻辑远离触发器(也就是说，并不是所以的ASIC库都有内置的同步复位逻辑，综合工具可能把符合逻辑综合到触发器自身之外)。例如对于带同步复位和加载使能的触发器，代码如下所示：

 　　　　　　　　　　　　　　　　　　

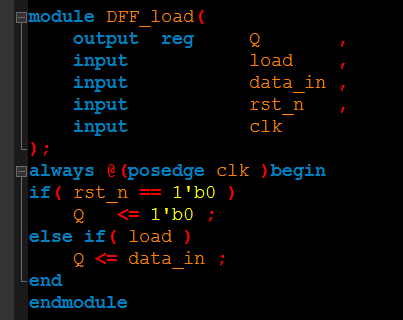
综合得到的电路图如下所示，左边是理想的电路，右边是可能综合出的电路:

   

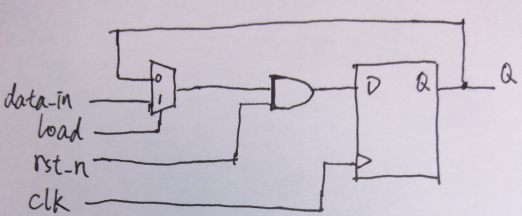
这两个电路的功能完全一样，只不过右边电路的复位控制逻辑(即复位与门)在多路复用器之外，也就是远离了触发器。这在门级仿真的时候(注意这是仿真)，当....

　　解决方法就是:一方面这个只是综合工具的问题，一般综合工具会自动识别在敏感列表里面又在条件表达式信号中的第一个信号为复位信号;另一方面，可以在RTL代码编写的时候，加入相关的综合指令，让综合的时候把复位逻辑靠近触发器。

　　

　　②由于同步复位需要在时钟沿的触发下才能起作用，复位信号是以短脉冲的方式出现时，时钟沿就有可能错失这个复位信号，导致复位脉冲丢失，同步复位电路没有起到作用，时序图如下所示：

 　　　　　　　　　　　　　　　　

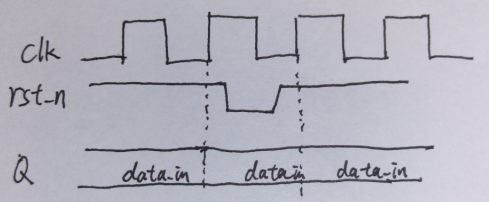
　　解决办法:一方面，可以采用脉冲捕捉电路，这个电路在我的跨时钟域控制信号传输中有讲到。;另一方面，可以将复位信号进行脉冲扩展，维持足够长的时间，这个可以通过一个小的计数器实现，如下图所示:

 　　　　　　　　　　　　　  　

　　③同步复位可能有组合逻辑延时，当复位逻辑距离触发器比较远时，这个时候就不能把触发器当做即时响应复位信号的触发器，而是有一定延时的触发器，这个时候就有了复位信号偏移的问题，关于复位信号偏移的描述，我们将在异步复位中进行描述。

　　解决方法:使用内置的同步复位触发器;综合的时候加入相关的综合指令，这个和①类似。

 

　　④我们前面说过，在由内部组合逻辑的产生复位信号的设计中，推荐使用同步复位。其实这也是有缺点的，这是因为这样产生复位信号的组合逻辑一方面在仿真的时候容易出现x态，另一方面在实际电路中，这样的复位信号容易被外部(多个)信号影响。

　　解决方法:不建议使用内部产生的复位信号;使用异步复位。

 

　　⑤门控时钟的同步复位可能无效:

　　使用门控时钟的时候，由于复位信号依赖于时钟，在复位信号发出的时候，时钟可能关闭了，这个时候就会导致实际的电路没有被复位，如下图所示:

 　　   

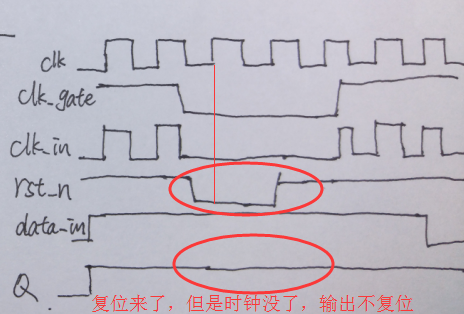
　　解决方法:只能使用异步复位，并在时钟恢复前移除异步复位。

 

　　⑥总线设计中的同步复位问题:

　　在总线控制中，系统上电复位的时候，我们要求不同芯片之间的总线工作在合理的状态上(比如处于高阻态或者输出);然而上电之后，由于系统时钟可能仍未正常工作，上电(同步)复位就可能无效，这个时候各个模块(芯片)就可能不会把总线接口设置为特定的状态，(当多个模块同时输出数据到总线上时)就可能导致电平冲突，严重的话会烧坏接口。

　　解决办法:为了防止芯片上电时内部总线出现竞争，有一下两种解决办法，一种是采用异步上电复位，如下图所示:

 　　　　　　　　　　　　

　　　　　　　　　　这个时候使用了异步复位，使能信号oe输出0，也就是有了初始的状态

　　另一种方法是使用复位信号能直接撤销三态使能的电路，如下所示:

 　　　　　　　　　　

从电路图中可以看到复位信号一方面控制了复位逻辑，另一方面控制了三态的使能端;这种技术简化了复位-高阻这个条路径的时序分析。

 

 

3.异步复位

(1)异步复位电路

　　异步复位触发器则是在设计触发器的时候加入了一个复位引脚，也就是说复位逻辑集成在触发器里面。(一般情况下)低电平的复位信号到达触发器的复位端时，触发器进入复位状态，直到复位信号撤离。带异步复位的触发器电路图和RTL代码如下所示:

 

 

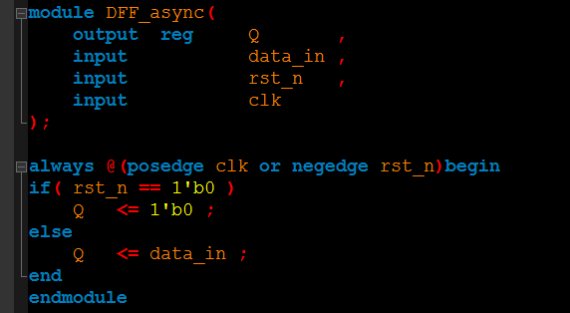
(2)异步复位的优点

　　①使用异步复位的最大好处就是复位路径上没有延时，如上面的图所示，复位信号一直连接到触发器的复位端口，而不是像同步复位那样需要经过一个复位控制逻辑(如与门)。这样子就减少了外界信号的影响。

　　②与时钟没有关系，不管时钟上升沿有没有到来，只要复位信号一有效，触发器就会复位，也就是基本上做到实时性；由于与时钟没有关系，因此也可以用在门控时钟里面。

　　③综合工具能自动推断出异步复位而不必加入任何综合指令。

 

(3)异步复位的缺点

　　①复位撤离问题

　　在介绍复位撤离问题之前，先说一下复位恢复时间和去除时间。所谓的复位恢复时间是指撤离一个复位信号时，复位信号从有效跳变为无效的时刻  与  下一个有效时钟沿  之间的这段时间；去除时间是指撤离一个复位信号时，复位信号从有效跳变为无效的时刻  与  上一个有效时钟沿  之间的这段时间（可以类比于触发器的建立时间和保持时间）。如下图所示:

 　　　　　　　　　　

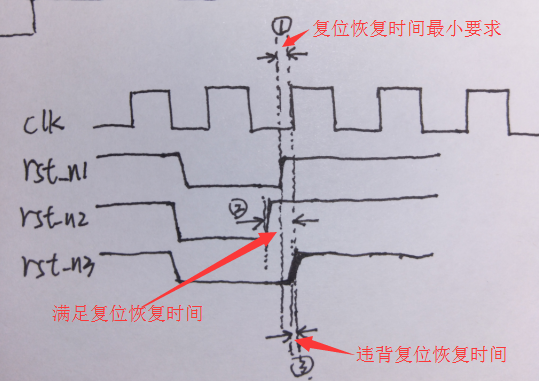
　　　　　　上图中，rst_n1是要求的复位恢复时间，rst_n2满足复位恢复时间，rst_n3复位恢复时间不足。

 　　　　　　　　　　

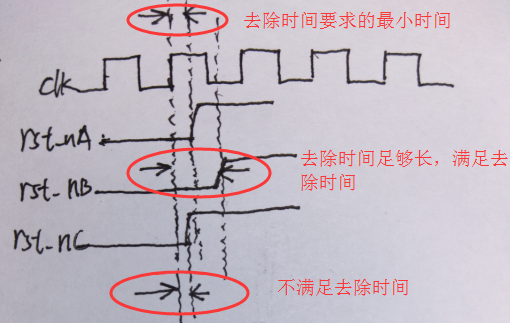
　　　　　　上图中，rst_nA是要求的复位去除时间，rst_n2满足复位去除时间，rst_n3复位去除时间不足。

　　从上面的两个图中可以知道，如果你想让某个时钟沿起作用（也就是采数据），那么你就应该在“恢复时间”之前让异步控制信号变无效；如果你想让某个时钟沿不起作用（也就是在这个时钟沿依旧复位），那么你就应该在“去除时间”过后使控制信号变无效。异步复位信号的恢复和去除时间需要大于一定的时间，如果你的异步复位信号在这两种情况之间（撤离），那么就没法确定时钟沿是否起作用了，即判断不出是复位还是不复位（不复位即是D触发器才输入端的数据）。

　　介绍了复位恢复时间和去除时间之后，我们就可以看看异步复位信号的问题了。由于异步复位信号与系统时钟毫无关系，复位可以在随时施加，也可以随时撤离。在施加的时候复位信号的时候，不存在任何问题，因为这跟复位恢复时间扯不上关系。但是，在撤离复位信号的情况下就有问题了，主要有两个问题:

　　·当异步复位信号的撤离时刻在时钟有有效沿附近时，就可能导致恢复时间或去除时间不足，即这个时候违背了复位恢复时间或去除时间，这时就可能导致触发器的输出端为亚稳态（注意是可能），如下所示:

 　　　　　　　　　　

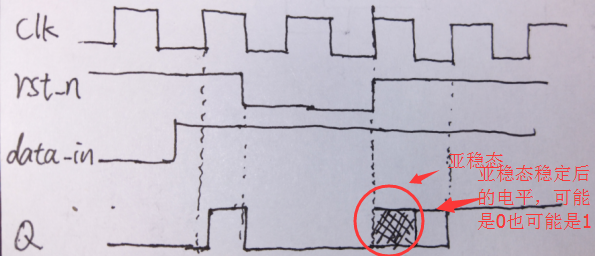
　　但是并不是所有情况都会产生亚稳态，当复位值和此时的的输出相同时，就不会产生亚稳态，如下图所示：

 　　　　　　　　　　

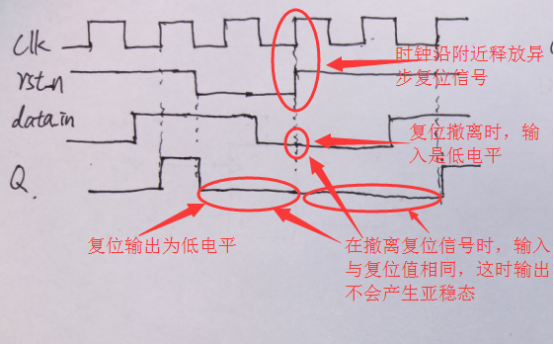
这是因为：复位信号翻转的时候，如果复位信号判断是低电平，输出就复位即一定是低电平；如果判断复位信号是高电平，输出信号就等于对输入信号的采样值。图里面输入信号就是低电平，不管你是复位还是不复位，输出一直是低电平，没有亚稳态。

 

　　·复位状态不一致的问题:

　　复位信号很时钟信号一样，复位通过复位网络到达各个触发器。一方面，复位网络具有非常大的扇出和负载，到达不同的触发器存在不同的延时，也就是存在复位偏移，因此撤离异步复位的时刻也是不一样的;另一方面，由于时钟网络也存在时钟偏移。这个时候异步复位信号就有可能在不同的触发器的不同时钟周期内进行撤离，也就是说异步复位的信号不一致，如下图所示:

 　　　　　　　　　　

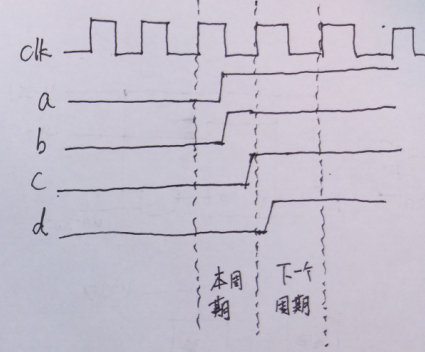
　　异步复位信号a是异步复位信号源，异步复位信号b、c、d是到达触发器的异步信号。我们可以看到，b信号是在本周期就撤离了复位;c信号则由于复位恢复时间不满足，则可能导致触发器输出亚稳态;而d信号则由于延时太长（但是满足了复位去除时间），在下一个周期才撤离复位。

　　

　　撤离问题的解决方法:异步复位的同步释放

　　异步复位的同步释放电路也称为复位同步器，这个方法是将外部输入的异步复位信号进行处理，产生另外一个适合用于后面电路的复位信号，这个处理后的复位信号能够异步复位电路中的触发器，又不会存在撤离问题（因为经过了同步）；这个异步复位同步释放的处理电路和RTL代码如下所示:

 　　　　　　　　　　　　　　　　

　　　　　　

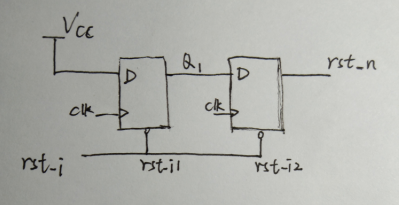
从图中可以看到，这是用外部异步复位信号来复位一对触发器，这对触发器异步地驱动主复位信号，也就是这对触发器产生电路需要的复位信号，这些复位信号再到达各个触发器，然后进行复位，理想的异步复位同步释放的时序如下所示:

 　　　　　　　　

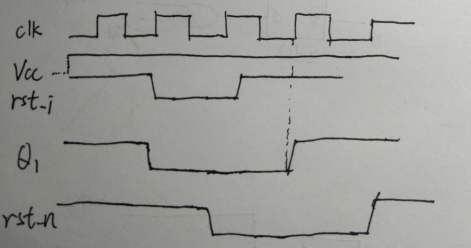
上图中，在理想的情况下，复位信号在两级D触发器上面的撤离时间可能不一样，这个和复位信号传输到的触发器位置和触发器的时钟沿有关。理想情况下的复位信号传输到目标触发器都能够同时撤离，并且不在时钟有效沿附近。

　　实际情况一般不是那么理想的，当不是理想的情况下，也就是说复位信号到达目标寄存器存在时钟偏移，并且复位信号有可能在时钟有效沿附近撤离，这个时候复位器出现的问题就有三种：第一级OK，第二级出现问题；第一级出现问题，第二级OK；两级都出现问题。下面我们就来看看这三种情况下产生的复位信号是什么情况：

　　第一级的撤离没有问题，第二级的撤离出现在时钟的有效沿附近，也就是说第二级的D触发器的撤离时间不满足复位恢复时间或者去除时间，这时候的时序图如下所示:

 　　　　　　　　

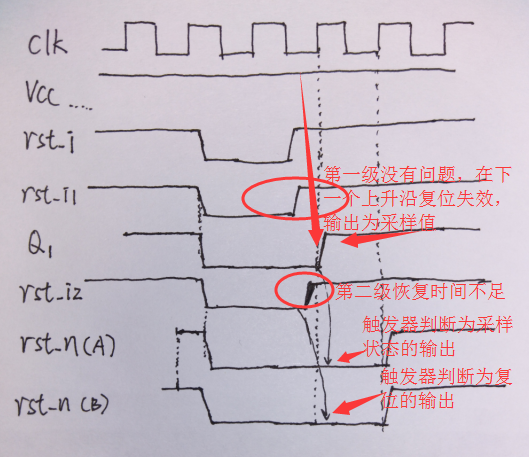
我们可以看到无论是触发器判断此刻是复位还是不复位，输出都是一样的，也就是说，输出rst_n不是亚稳态，而是确定的值。

 

　　第一级的撤离出现问题，第二级的撤离没有问题，这时候的时序图如下所示：

 　　　　　　

我们可以看到，第一级触发器虽然产生了亚稳态，但是由于第二级触发器的存在，亚稳态并没有传播下去，得到的复位信号依然是干净的，只不过这个复位信号可能延长多一个周期而已（这是因为亚稳态稳定后的可能态引起的）。

 

　　最极端的一种情况是，两级的撤离都不满足复位恢复时间或者去除时间，这时候的时序图如下所示：

 　　　　　　

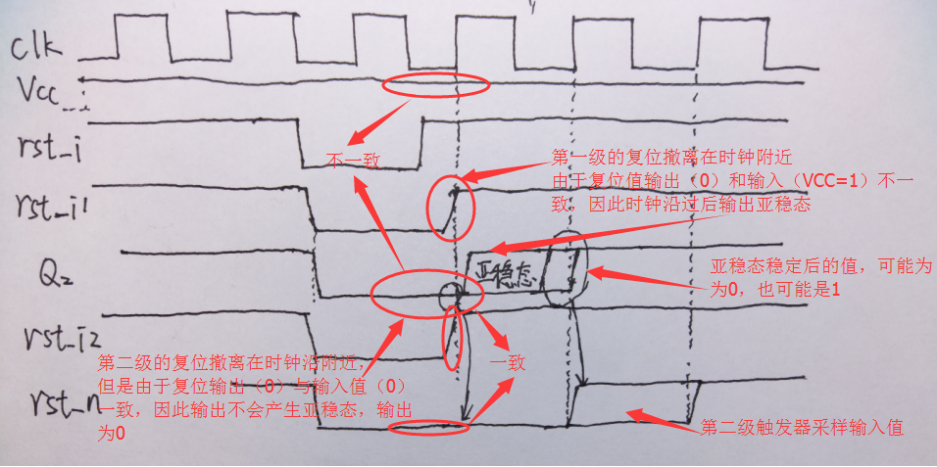
我们可以看到第一级触发器产生了亚稳态，但是由于第二级触发器的存在，亚稳态没有传播下去；虽然第二级触发器的复位信号撤离也在时钟有效沿附近，但是跟第一种情况一样，第二级触发器是不会产生亚稳态的。因此即使是极端状态，输出的复位信号也是干净的。

　　由此我们可以看到，异步复位的同步撤离能够有效地解决撤离导致的复位恢复时间或者去除时间不足的问题，同时把复位信号同步化，解决了复位撤离偏移的问题。

 

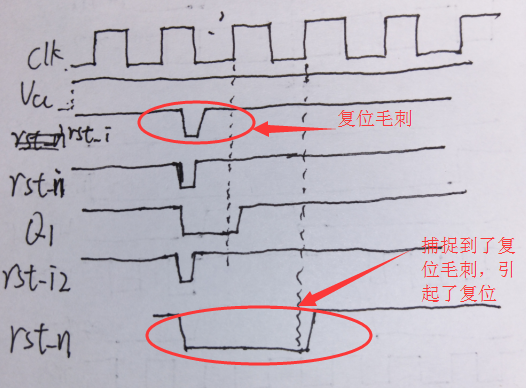
　　②异步复位的抖动问题

　　当外部输入的异步复位信号产生毛刺时，任何满足触发器最小复位脉冲宽度的输入都有可能引起触发器复位，这问题是源头上的问题，即使是使用上面的同步器，也还是有同样的敏感问题，时序图如下所示：

 　　　　　　　　　　　　　　

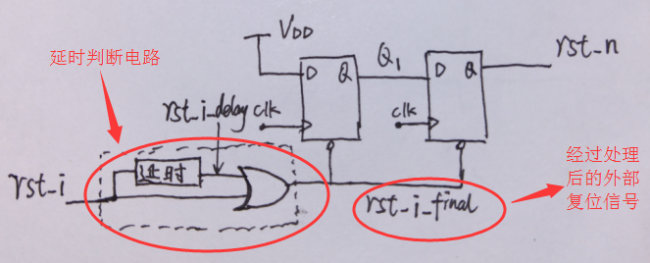
　　解决方法：一个是使用同步复位，另一个就是过滤毛刺了，过滤毛刺和消抖的思路有点像，主要就是经过一段延时之后，在经过逻辑门判断产生外部来的是不是真正复位信号，加上过滤毛刺信号部分的同步撤离电路和时序如下所示：

 　　　　　　　　　　　　

　　　　　　　　　　　　　　   　　

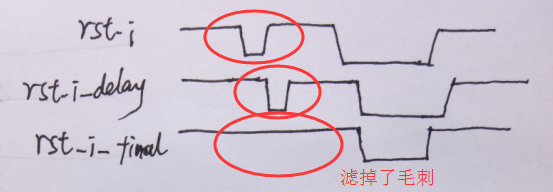
在上图中，我们可以看到，抖动问题得到了解决。然而这种方法还是有缺点的，主要就是这个延时电路的延时控制可能随着环境而变化，而且延时的时间要合适长才行，绝对不能太短。

 

　　③DFT的问题

　　在DFT的时候，如果异步复位信号不能直接被I/O引脚驱动，就必须将异步复位线和后面的的被驱动电路断开，用来保证DFT扫描和测试能够正确进行。总之异步复位增加了DFT的复杂性。

 

 

4.复位策略——复位网络

　　在数字电路里面，复位信号驱动了很多触发器，仅次于时钟，因此复位也往往形成或者使用复位网络。复位网络的设计也是有值得斟酌的地方，例如，由于复位的扇出太大，全部的复位不能仅仅由一个端口驱动，也就是不能像下面一样：

 　　　　　　　　　　　　　　　　

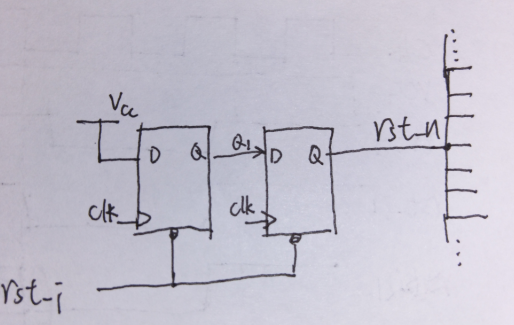
　　既然上面的不行，那就改成下面的呗，也就是使用多各“并联”的同步释放，分担一下负载压力：

 　　　　　　　　　　　　　　　　

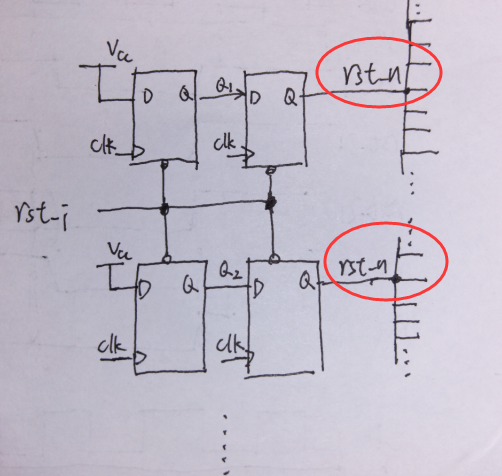
　　然而这种方案还是有问题的，这是第一级的撤离出现问题，第二级的撤离没有问题的时候，亚稳态稳定后的状态可能不一样，导致rst_n的复位不一致，有的复位可能会快/慢一个周期。

　　最后的方案是，先进行同步释放之后，同步后的复位信号又当做各个部分的异步信号，然后进行同步释放，如下所示：

 　　　　　　　　　　　　

这样先经过前级的同步释放之后，就不存在亚稳态稳定好导致的输出rst_n不一致的问题了。

 

　　最后说一下多时钟域的复位：在多时钟域复位中，外部的异步复位信号的同步释放应该各自的时钟进行同步，比如异步FIFO中，写时钟域就用写时钟进行同步释放；读时钟域就用读时钟进行同步释放。