树篇2-平衡二叉查找树之AVL树

一、AVL树定义

        在数据结构中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度差的绝对值不能超过一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次旋转来使得AVL树保持平衡。

二、AVL树的特性

1.任意一个根节点的左孩子小于根节点，右孩子大于根节点。

2.每个结点的左右子树的高度之差的绝对值不能超过1。

三、如何处理插入节点或删除节点引起的不平衡问题

        在写这篇博客之前，看了许多关于AVL树的资料。有的将处理不平衡问题归纳为左左、左右、右左、右右处理不平衡问题，在此基础上又进行划分，看的我头晕目眩。经过大量的查找，一种最简单有效、好理解、容易接受的方法是将上面的四种情况归纳为两种，与右有关的旋转统一归纳到顺时针旋转，与左有关的旋转统一归纳到逆时针旋转。

四、插入操作

        AVL树的插入操作首先会按照普通搜索二叉树的插入操作进行，当插入一个数据后，我们会沿着插入数据时所经过的的节点回溯，回溯的过程中会判回溯路径中的每个节点的左子支高度与右子支高度之差的绝对值是否超过1，如果超过1我们就进行调整，调整的目的是使得该节点满足AVL树的定义。调整的情况可以分为以下四旋转操作，旋转操作可以降低树的高度，同时不改变搜索二叉树的性质（即任何一个节点左子支中的全部节点小于该节点，右子支的全部节点大于该节点）。

五、节点不平衡解决策略

情况1  左左(LL)

        节点N左子支比右子支高度大2，且插入的节点位于N的左孩子节点NL的左子支上

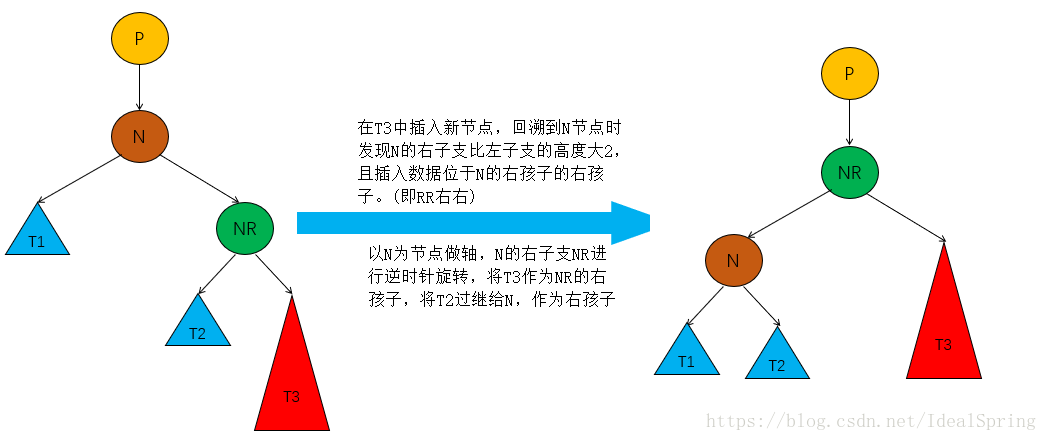
情况2  右右(RR)

        节点N右子支比左子支高度大2，且插入的节点位于节点N右孩子节点NR的右子支上

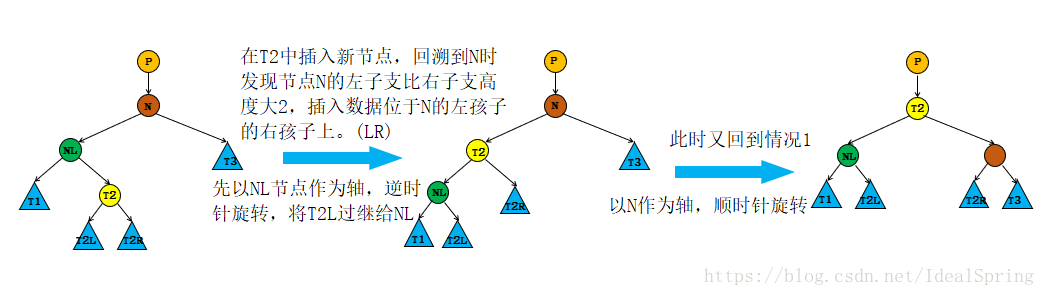
情况3  左右(LR)

节点N左子支比右子支高度大2，且插入的节点位于节点N左孩子节点NL的右子支上

情况4  右左(RL)

节点N左子支比右子支高度大2，且插入的节点位于节点N左孩子节点NL的右子支上

六、AVL删除操作

        AVL树的删除操作和插入操作一样，首先会按照普通搜索二叉树的删除操作进行，当删除一个数据后，和插入操作一样，我们通常采取的策略是沿着删除数据时所经过的的节点回溯，回溯的过程中会判断该节点的左子支高度与右子支高度之差的绝对值是否超过1（或者说大2），如果超过1，我们就进行调整，调整的目的是使得该节点满足AVL树的定义。调整的情况可以分为四种，和插入过程完全一样，这里不在赘述。

七、完整代码实现

import com.sun.org.apache.regexp.internal.REUtil;

import java.util.Comparator;

/**
 * AVL树：自平衡二叉搜索树
 */
public class AVLTree<E> {
    /**
     * AVL树节点
     */
    private class AVLTreeNode<E> {
        int height; // 节点高度
        E element;  // 值域
        AVLTreeNode<E> parent;  // 父节点
        AVLTreeNode<E> leftChild;   // 左孩子
        AVLTreeNode<E> rightChild;  // 右孩子

        // 构造方法
        public AVLTreeNode(int height, E element, AVLTreeNode<E> parent, AVLTreeNode<E> leftChild, AVLTreeNode<E> rightChild) {
            this.height = height;
            this.element = element;
            this.parent = parent;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
        }

        @Override
        public String toString() {
            return "AVLTreeNode{" +
                    "height=" + height +
                    ", element=" + element +
                    '}';
        }
    }

    //创建一个伪根节点，该节点的右子支才是真正的AVL树的根
    //使用伪根节点节点的目的是，对插入和删除操作递归的形式能够统一
    private AVLTreeNode<E> rootIndex;    // 指向根节点的伪根节点(目的：方面操作)
    private int size;   // 节点个数
    private Comparator<? super E> comparator;   //节点大小比较器

    /**
     * 默认比较器
     */
    private class Cmp<T> implements Comparator<T> {
        @Override
        public int compare(T e1, T e2) {
            return ((Comparable)e1).compareTo(e2);
        }
    }

    // 不带参数的构造方法
    public AVLTree() {
        this.comparator = new Cmp<>();
        this.rootIndex = new AVLTreeNode<>(-1, null, null, null, null);
    }

    // 带比较器构造方法
    public AVLTree(Comparator<? super E> comparator) {
        if (comparator == null) // 如果比较器为空，抛出非法参数异常
            throw new IllegalArgumentException();

        this.comparator = comparator;
        this.rootIndex = new AVLTreeNode<>(-1, null, null, null, null);
    }

    // 返回元素个数
    public int getSize() {
        return size;
    }

    // 插入元素
    public void insert(E e) {
        if (e == null)
            throw new IllegalArgumentException("插入节点不能为空!");

        insert(rootIndex.rightChild, e);
    }
    // 插入节点内部方法
    private void insert(AVLTreeNode<E> node, E e) {
        // 这个if，在整个生命周期中只执行一次
        if (node == null) { //伪根节点的右孩子为空，即真实的根节点为空。将插入的节点设置为根节点
            rootIndex.rightChild = new AVLTreeNode<>(1, e, rootIndex, null, null);
            size++;
            return;
        }

        if (comparator.compare(e, node.element) < 0) {  // 待插入元素小于当前节点
            if (node.leftChild != null) {
                insert(node.leftChild, e);
                int leftHeight = getNodeHeight(node.leftChild);
                int rightHeight = getNodeHeight(node.rightChild);

                if (leftHeight - rightHeight == 2) {
                    if (comparator.compare(e, node.leftChild.element) < 0) {
                        clockwiseRotate(node);
                    } else {
                        antiClockwiseRotate(node.leftChild);
                        clockwiseRotate(node);
                    }
                }
            } else {    // 创建节点，将新节点作为node节点左孩子
                size++;
                node.leftChild = new AVLTreeNode<>(1, e, node, null, null);
            }
        } else if (comparator.compare(e, node.element) > 0) {  // 待插入元素大于当前节点
            if (node.rightChild != null) {
                insert(node.rightChild, e);
                int leftHeight = getNodeHeight(node.leftChild);
                int rightHeight = getNodeHeight(node.rightChild);

                if (rightHeight - leftHeight == 2) {
                    if (comparator.compare(e, node.rightChild.element) > 0) {
                        antiClockwiseRotate(node);
                    } else {
                        clockwiseRotate(node.rightChild);
                        antiClockwiseRotate(node);
                    }
                }
            } else {
                size++;
                node.rightChild = new AVLTreeNode<>(1, e, node, null, null);
            }
        } else if (comparator.compare(e, node.element) == 0){  // 待插入元素等于当前节点
            //元素已存在，我们用新的元素更新旧
            node.element = e;
        }

        node.height = Math.max(getNodeHeight(node.leftChild), getNodeHeight(node.rightChild)) + 1;
    }

    /**
     * 顺时针旋转(右旋)
     *
     * @param node 表示要旋转的轴节点
     */
    private void clockwiseRotate(AVLTreeNode<E> node) {
        AVLTreeNode<E> nodeParent = node.parent;    // 轴节点的父节点
        AVLTreeNode<E> nodeLeftChild = node.leftChild;  // 轴节点的左孩子

        // 第一步：父节点不动，顺时针旋转轴节点；
        //         将老轴节点的左孩子作为新的轴节点，并将新轴节点的父亲指向老轴节点的父亲
        if (nodeParent.leftChild == node)   // node节点为父节点左孩子，则将旋转后的轴节点(nodeLeftChild)作为父节点左孩子
            nodeParent.leftChild = nodeLeftChild;   // 将node的左孩子作为node父节点左孩子
        else    // node节点不是父节点左孩子，则将旋转后的轴节点(nodeLeftChild)作为父节点右孩子
            nodeParent.rightChild = nodeLeftChild;  // 将node的左孩子作为node父节点的右孩子
        nodeLeftChild.parent = nodeParent;  // 将node的左孩子父节点指针指向新的父节点

        // 第二步：将新轴节点的右孩子过继给老轴节点作为它的左孩子
        node.leftChild = nodeLeftChild.rightChild;  // node左孩子的右孩子过继给node作为左孩子
        if (nodeLeftChild.rightChild != null)   // 如果node左孩子的右孩子存在，将它的父节点指向node
            nodeLeftChild.rightChild.parent = node;

        // 第三步：将新轴节点指向老轴节点
        nodeLeftChild.rightChild = node;    // 将新的轴节点的右孩子指向老轴节点
        node.parent = nodeLeftChild;    // 将老轴节点的父亲指向新轴节点

        // 旋转后要更新被替代的老轴节点的高度和新轴节点的高度(计算规则：其节点左右子树的最大高度+1)
        node.height = Math.max(getNodeHeight(node.leftChild), getNodeHeight(node.rightChild)) + 1;
        nodeLeftChild.height = Math.max(getNodeHeight(nodeLeftChild.leftChild), getNodeHeight(nodeLeftChild.rightChild)) + 1;
    }

    /**
     * 逆时针旋转(左旋)
     *
     * @param node 表示要旋转的轴节点
     */
    private void antiClockwiseRotate(AVLTreeNode<E> node) {
        AVLTreeNode<E> nodeParent = node.parent;    // 老轴节点父节点
        AVLTreeNode<E> nodeRightChild = node.rightChild;    // 老轴节点的右孩子，即要替代老轴节点的新轴节点

        // 第一步：父节点不动，逆时针旋转轴节点；
        //         将老轴节点的右孩子作为新的轴节点，并将新轴节点的父亲指向老轴节点的父亲
        if (nodeParent.leftChild == node) { // 如果老轴节点是其父亲的左孩子，将新轴节点也作为它的左孩子
            nodeParent.leftChild = nodeRightChild;
        } else
            nodeParent.rightChild = nodeRightChild;
        nodeRightChild.parent = nodeParent;

        // 第二步：将新轴节点的左孩子过继给老轴节点作为它的右孩子
        node.rightChild = nodeRightChild.leftChild; // node右孩子的左孩子过继给node作为右孩子
        if (nodeRightChild.leftChild != null)   // 如果node右孩子的左孩子存在，将它的父节点指向node
            nodeRightChild.leftChild.parent = node;

        // 第三步：将新轴节点指向老轴节点
        nodeRightChild.leftChild = node;    // 将新的轴节点的左孩子指向老轴节点
        node.parent = nodeRightChild;   // 将老轴节点的父亲指向新轴节点

        // 旋转后要更新被替代的老轴节点的高度和新轴节点的高度(计算规则：其节点左右子树的最大高度+1)
        node.height = Math.max(getNodeHeight(node.leftChild), getNodeHeight(node.rightChild)) + 1;
        nodeRightChild.height = Math.max(getNodeHeight(nodeRightChild.leftChild), getNodeHeight(nodeRightChild.rightChild)) + 1;
    }

    // 返回节点的高度
    private int getNodeHeight(AVLTreeNode<E> node) {
        if (node == null)
            return 0;
        else
            return node.height;
    }

    // 逐层遍历
    public void orderTraverse() {
        if (rootIndex != null)
            orderTraverse(rootIndex.rightChild);
    }

    private void orderTraverse(AVLTreeNode<E> node) {
        if (node != null) {
            System.out.print(node.element + "-" + node.height + "		");
            if (node.leftChild != null)
                System.out.print( "(L)" + node.leftChild.element + "		");
            else
                System.out.print("(L)Null		");

            if (node.rightChild != null)
                System.out.print("(R)" + node.rightChild.element + "		");
            else
                System.out.print("(R)Null		");

            System.out.println();
            orderTraverse(node.leftChild);
            orderTraverse(node.rightChild);
        }
    }

    // 移除指定节点
    public boolean removeNode(E e) {
        return removeNode(rootIndex.rightChild, e);
    }

    private boolean removeNode(AVLTreeNode<E> node, E e) {
        if (node == null)   // 没有找到待删除节点(递归结束条件)
            return false;

        if (comparator.compare(e, node.element) < 0) {  // 待删除元素小于当前节点
            boolean flog = removeNode(node.leftChild, e);   // 向左节点继续找，继续递归
            if (flog == false)  // 没找到结束递归返回
                return false;

            // 调整树，使它满足AVL树条件
            int leftHeight = getNodeHeight(node.leftChild);
            int rightHeight = getNodeHeight(node.rightChild);
            if (rightHeight - leftHeight == 2) {    // 高度差为2表示此节点为失衡节点，需要旋转平衡
                // 失衡节点node，由于node节点右子树元素过多导致失衡，调节右子树，以完成平衡化处理
                // 大于代表node的右子树的右子树节点深度大导致的失衡，直接逆时针旋转即可解决
                // 小于代表node的右子树的左子树节点深度大导致的失衡，先以node的右子节点顺时针旋转，再以node逆时针旋转
                if (getNodeHeight(node.rightChild.rightChild) > getNodeHeight(node.rightChild.leftChild)) {
                    antiClockwiseRotate(node);
                } else {
                    clockwiseRotate(node.rightChild);
                    antiClockwiseRotate(node);
                }
            }
        } else if (comparator.compare(e, node.element) > 0) {   // 待删除元素大于于当前节点
            boolean flog = removeNode(node.rightChild, e);  // 向右节点继续找，继续递归
            if (flog == false)  // 没找到结束递归返回
                return false;

            // 调整树，使它满足AVL树条件
            int leftHeight = getNodeHeight(node.leftChild);
            int rightHeight = getNodeHeight(node.rightChild);
            if (leftHeight - rightHeight == 2) {
                if (getNodeHeight(node.leftChild.leftChild) > getNodeHeight(node.leftChild.rightChild)) {
                    clockwiseRotate(node);
                } else {
                    antiClockwiseRotate(node.leftChild);
                    clockwiseRotate(node);
                }
            }
        } else {    // 待删除节点等于当前节点(找到要删除的节点)
            AVLTreeNode<E> nodeParent = node.parent;

            // 分情况讨论：
            // 1.左子支为空，可直接删除，在这一层一定不需要旋转
            if (node.leftChild == null) {
                size--;
                if (nodeParent.leftChild == node) {
                    nodeParent.leftChild = node.rightChild;
                    if (nodeParent.leftChild != null)
                        nodeParent.leftChild.parent = nodeParent;
                } else {
                    nodeParent.rightChild = node.rightChild;
                    if (nodeParent.rightChild != null)
                        nodeParent.rightChild.parent = nodeParent;
                }
            }
            // 2.右子支为空，可直接删除，在这一层一定不需要旋转
            else if (node.rightChild == null) {
                size--;
                if (nodeParent.leftChild == node) {
                    nodeParent.leftChild = node.leftChild;
                    if (nodeParent.leftChild != null)
                        nodeParent.leftChild.parent = nodeParent;
                } else {
                    nodeParent.rightChild = node.leftChild;
                    if (nodeParent.rightChild != null)
                        nodeParent.rightChild.parent = nodeParent;
                }
            }
            // 3.左右子支都存在，找到待删除的节点,用后继节点代替，然后删除后继节点
            // 删除后继节点策略：找到待删除节点的后继节点，将后继节点的值替代删除节点的值，以达到删除该值的目的
            // 随后，再使用removeNode方法移除后继节点。这种策略很简单，比我上一篇博客中寻找节点的方式简单多了。
            else {
                E nextNodeElement = treeMinNode(node.rightChild);  // 找node节点的后继节点
                node.element = nextNodeElement; // 将后继节点值替代删除的节点值
                removeNode(node.rightChild, nextNodeElement);   // 删除后继节点

                int leftHeight = getNodeHeight(node.leftChild);
                int rightHeight = getNodeHeight(node.rightChild);
                if (leftHeight - rightHeight == 2) {
                    if (getNodeHeight(node.leftChild.leftChild) > getNodeHeight(node.leftChild.rightChild)) {
                        clockwiseRotate(node);
                    } else {
                        antiClockwiseRotate(node.leftChild);
                        clockwiseRotate(node);
                    }
                }
            }


        }

        // 更新节点的高度
        node.height = Math.max(getNodeHeight(node.leftChild), getNodeHeight(node.rightChild)) + 1;
        return true;
    }

    // 求某个节点作为根时，该子树的最小值
    private E treeMinNode(AVLTreeNode<E> node) {
        while (node.leftChild != null)
            node = node.leftChild;
        return node.element;
    }

}

测试代码：

public class AVLTreeDemo {
    public static void main(String[] args) {
        AVLTree<Integer> tree = new AVLTree<>();
        tree.insert(150);
        tree.insert(90);
        tree.insert(250);
        tree.insert(200);
        tree.insert(300);
        tree.insert(210);
        tree.insert(205);
        tree.insert(80);

        tree.orderTraverse();
        System.out.println("Number of element in the tree: " + tree.getSize());
        System.out.println();

        tree.removeNode(150);
        tree.orderTraverse();
        System.out.println("Number of element in the tree: " + tree.getSize());
        System.out.println();

        tree.removeNode(200);
        tree.removeNode(250);
        tree.orderTraverse();
        System.out.println("Number of element in the tree: " + tree.getSize());
        System.out.println();
    }
}

运行结果：

200-4        (L)90        (R)250        
90-2        (L)80        (R)150        
80-1        (L)Null        (R)Null        
150-1        (L)Null        (R)Null        
250-3        (L)210        (R)300        
210-2        (L)205        (R)Null        
205-1        (L)Null        (R)Null        
300-1        (L)Null        (R)Null        
Number of element in the tree: 8

200-4        (L)90        (R)250        
90-2        (L)80        (R)Null        
80-1        (L)Null        (R)Null        
250-3        (L)210        (R)300        
210-2        (L)205        (R)Null        
205-1        (L)Null        (R)Null        
300-1        (L)Null        (R)Null        
Number of element in the tree: 7

205-3        (L)90        (R)300        
90-2        (L)80        (R)Null        
80-1        (L)Null        (R)Null        
300-2        (L)210        (R)Null        
210-1        (L)Null        (R)Null        
Number of element in the tree: 5