1.定义
![]()
2.求解特征值

求解特征方程即可得到特征值
3.特征向量求解
( left(lambda I-A ight)x=0)


4.矩阵的秩和特征值的关系
4.矩阵的特征值分解
特征值分解是将一个矩阵分解成下面的形式:
(A=Qsum Q^{-1})
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。
5.矩阵的含义[1]
一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:
它其实对应的线性变换是下面的形式:
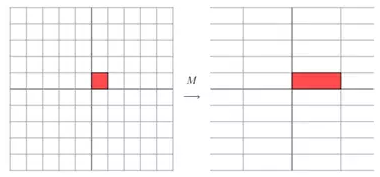
因为这个矩阵M乘以一个向量(x,y)的结果是:
当矩阵不是对称的时候,假如说矩阵是下面的样子:
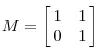
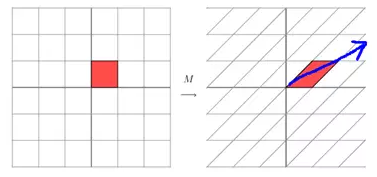
特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
[1]http://mp.weixin.qq.com/s?__biz=MzA5ODUxOTA5Mg==&mid=401860790&idx=1&sn=8720a2a1d83f407087b665c753fc9fc9&scene=1&srcid=0811KwT9hjyqcbJYMISXaLbc#rd