树链剖分学习笔记

我们所常说的树链剖分其实是轻重链剖分
树链剖分可以处理树上的任意两点间路径和任意一点子树的信息修改与查询(配合线段树这样的数据结构..)

建议先学会线段树和 LCA。

首先注意下文中权值是赋在点上的 而不是在边上
如果遇到权值在边上的情况 把权值赋给这条边连接的两点中深度较大的那个点即可

1.引入

线段树是通过维护一些区间 并且把待处理区间拆分成一定数量个维护的区间
树链剖分思想相似 将树剖分成(log n)级别条互相不相交的链 同时保证每一个点都在且仅在一条链上(所有链可以覆盖所有点) 对于每一条路径可以将其拆分成(log n)级别条链分别维护链上点权
链就是一些点 这些点首尾相接 除了两端的点只有一个点与之相连 其他的点都有两点与之有边相连
在这里的链中 链维护一些深度递增的点 没有任意两点在树中深度相同
子树的问题在后文提到

2.思想

如果将一条很长的链一起处理 可以优化效率
为了使得链与链不相交 必定有一些边不能在链中 我们把这些边成为轻边 因为这样的边不会很多 遇到时直接处理就行了
于是我们通过一定形式将一棵树分成轻边和链 所有的链都一起处理 而对于轻边则直接一条一条边处理

就是为了把(n)变成(log n)啊

3.实现

1.预处理

我们把链称为重链
首先我们要让重链的取法最优
我们对于每一个点 显然它到它儿子(我们先随便指定一个点当做根)的所有出边中 只有一条边能在重链中 否则链会相交
在这里我们取子树大小最大的儿子作为重儿子 对于任意一个点该点和它的重儿子位于同一条重链上 到其余的儿子的路径作为轻边
这样就会形成一些重链了 如果觉得太抽象可以看看下面的图片

至于为什么取子树大小最大在后面复杂度证明中会提到

首先我们要通过dfs预处理出每一个点的子树大小、父亲节点编号、深度、重儿子编号。
这些都不难处理 在下面的代码中给出注释了

这时候这棵树已经剖分好了 但是为了维护链上信息 我们还要再处理一些信息
首先每一条链可以视为一个区间 我们可以用线段树来维护链信息

因此 我们需要给树上每一个点编号 代表它在线段树中的编号 因为每一条重链在线段树上必须对应一个连续的区间 而原来的顺序未必能满足这个要求
其次再建立一个数组维护线段树上编号为i的点对应原树上的点的编号 在线段树建树时会用到
所以我们要再dfs一遍 而且这个dfs的遍历顺序要稍微调整一下 通过每一次先遍历点的重儿子再遍历其他儿子来保证每一条重链在线段树上必须对应一个连续的区间

等等 还没结束
现在我们是不知道每一条重链对应的区间编号
所以对于每一个点我们还要处理出它所在重链的顶端的点(该链上深度最小的点)编号

如果一个点在重链的中间 那么只用处理这条重链的一部分就行了(该点到顶端的部分) 链上的点对应线段树中编号是随深度递增的
如果路径上的两个点都在同一条重链上 只要处理这两个点之间的部分就行了

最后放张图方便理解 代码在最后

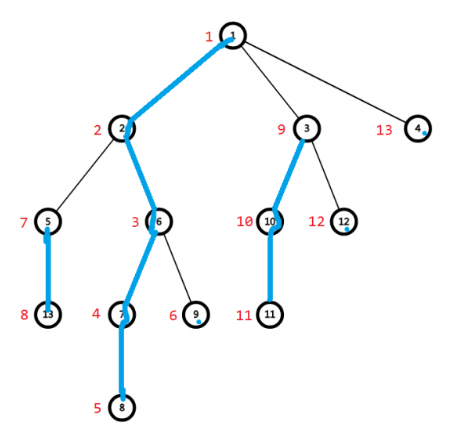
图中每一条蓝色的线就代表一条重链
1-2-6-7-8
5-13
3-10-11
4
9
12
注意后面三个点是一个点组成一条重链
红色数字代表它在线段树中对应编号

code:

void dfs1(int u,int f){
	// dfs1 传参 当前点和它的父亲
	int maxs = 0,v;
   // maxs记录当前点的最大子数的大小(大小为包含点数)
	siz[u] = 1; dep[u] = dep[f] + 1; fa[u] = f;
   // siz为该点为根的子数大小 先加上它自己
   // dep为该点深度
   // fa为该点父亲
	for(int i = hed[u];i;i = nxt[i]){
		v = to[i]; if(v == f) continue;
		dfs1(v,u); // 先遍历每个儿子节点
		siz[u] += siz[v]; // 修改自己的子树大小
		if(siz[v] > maxs){
        // 如果当前儿子子树大小比目前保存的值大 把该点重儿子更新为该点
			maxs = siz[v];
			son[u] = v;
		}
	}
}

inline void dfs2(int u,int f){
	// dfs2传参 u是当前点 f和上面不一样 f是当前点所在重链顶端的编号
	top[u] = f; // top代表u的重链顶端的编号
	id[u] = ++ cnt; // id代表该点在线段树中对应的编号
	rid[cnt] = u; // rid[cnt]=u代表线段树中编号为u的点对应树上编号为cnt的点
	if(!son[u]) return; // 叶子节点 不能搜索
	dfs2(son[u],f); // 先遍历重儿子 重儿子top是自己的top
	for(int i = hed[u];i;i = nxt[i]){
		int v = to[i];
		if(v == fa[u] || v == son[u]) continue;
		dfs2(v,v); // 遍历轻儿子(不是重儿子的儿子) 轻儿子链顶是它自己
	}
}
dfs1(s,0); dfs2(s,s);
// s为根 注意根节点所在重链顶端是它自己

2.链修改查询

x到y的树上路径一定为(x->LCA(x,y)->y)
这个过程相当于把一个点先移动到LCA 在把另一个点移动到LCA所在重链上 再处理这两点之间的部分
我们的目标状态是两个点移动到同一条重链上
每一次我们选择所在重链的顶端 深度最浅的点 修改/查询这个点到链顶端部分所有点的信息(这一段在线段树上一定是连续的) 并且把这个点移动到它所在链顶端的父亲节点
直到两点在同一条重链上
然后修改/查询两点之间的部分即可

查询还需要把那几条链的信息首尾拼接起来，求和或求最值的时候，合并就是所有链查询得到的数求和/取最值了，但有些时候可能会比较复杂，要用合并线段树左右儿子信息的方式合并链。

如果两点不在同一条重链上 这两点的LCA的所有儿子中一定有一个重儿子和大于等于一个非重儿子的子节点 这两个点在移动过程中必定会有一个点移动到重儿子所在链的链上 这样以后就会移动另一个点(之前那个点所在链顶端浅于或等于LCA)到某个轻儿子的父亲上 也就是移动到了LCA

code:

void update_chain(LL x,LL y,LL v){
	while(top[x] != top[y]){
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		update(1,1,n,id[top[x]],id[x],v);
		x = fa[top[x]];
	}
	if(dep[x] > dep[y]) swap(x,y);
	update(1,1,n,id[x],id[y],v);
}

3.子树修改查询

仔细想一想上面第二遍dfs的过程 不难发现对于任意一个点 在遍历这个点之后会先把这个点所在的整棵子树遍历完 再去遍历其他的点
所以啊 一个点对应的子树在线段树上对应的是一段连续的区间啊 这还不好处理吗

code:

void update_son(LL x,LL v){
	update(1,1,n,id[x],id[x] + siz[x] - 1,v);
    // 注意细节 -1
}

4.LCA查询

看完2应该就知道了
一样的处理方式 最后两个点移动到同一条重链上时较浅的点为LCA

code:

int lca(int x,int y){
	while(1){
		if(top[x] == top[y]) break;
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		x = fa[top[x]];
	}
	return (dep[x] > dep[y] ? y : x);
}

4.复杂度证明

取子树大小最大的儿子作为重儿子
所以从任意一点开始走 每走一条轻边 走完后的点子树大小相对于原来的点至少减少到原来一半
所以之多经过(logn)条轻边
然后由于重链是一起处理的 每经过一条重链后会再经过一条轻链 然后再经过下一条重链
相当于每一条重链都是在两条轻边之间的 所以重链条数也不会超过(log_2n)条
而且 显然这个上界比较松 跑不满

加上线段树的(logn) 树链剖分一次的复杂度为(log^2n)
树剖常数很小 n<=100000的时候可以吊打少一个log的LCT

5.完整代码

P3384模板题
古时候的代码了 现在码风都变了

#include <map>
#include <list>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define LL long long
#define mid ((l + r) >> 1)
#define lson (x << 1)
#define rson ((x << 1) | 1)
using namespace std;

LL n,q,r,N,a,b;
LL w[200005] = {0};
LL to[400005] = {0},hed[400005] = {0},nxt[400005] = {0},cnt = 0;
LL fa[200005] = {0},dep[200005] = {0},siz[200005] = {0},son[200005] = {0},top[200005] = {0},id[200005] = {0},rid[200005] = {0};

inline void add_edge(LL f,LL t){
	++ cnt;
	to[cnt] = t;
	nxt[cnt] = hed[f];
	hed[f] = cnt;
}

//SEGMENT TREE +
LL val[800005] = {0};
LL add[800005] = {0};
void build(int x,int l,int r){
    if(l == r){
        val[x] = w[rid[l]] % N;
        return;
    }
    build(lson,l,mid);
    build(rson,mid + 1,r);
    val[x] = (val[lson] + val[rson]) % N;
}

void push(int x,int l,int r){
    if(!add[x]) return;
    add[lson] += add[x]; val[lson] += (LL)(mid - l + 1) * add[x];
    add[rson] += add[x]; val[rson] += (LL)(r - mid) * add[x];
    add[lson] %= N; add[rson] %= N;
    val[lson] %= N; val[rson] %= N;
    add[x] = 0;
}

void update(int x,int l,int r,int L,int R,LL k){
    if(l >= L && r <= R){
    	add[x] += k; add[x] %= N;
    	val[x] += (LL)(r - l + 1) * k; val[x] %= N;
        return;
    }
    push(x,l,r);
    if(L <= mid) update(lson,l,mid,L,R,k);
    if(R > mid) update(rson,mid + 1,r,L,R,k);
    val[x] = (val[lson] + val[rson]) % N;
}

LL query(int x,int l,int r,int L,int R){
    LL sum = 0;
    if(l >= L && r <= R){
        return val[x];
    }
    push(x,l,r);
    if(L <= mid) sum = (sum + query(lson,l,mid,L,R)) % N;
    if(R > mid) sum = (sum + query(rson,mid + 1,r,L,R)) % N;
    return sum;
}
//SEGMENT TREE

//
inline void dfs1(LL u,LL f){
	register LL maxs = 0,v;
	siz[u] = 1; dep[u] = dep[f] + 1; fa[u] = f;
	for(register int i = hed[u];i;i = nxt[i]){
		v = to[i]; if(v == f) continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if(siz[v] > maxs){
			maxs = siz[v];
			son[u] = v;
		}
	}
}

inline void dfs2(LL u,LL f){
	top[u] = f;
	id[u] = ++ cnt;
	rid[cnt] = u;
	if(!son[u]) return;
	dfs2(son[u],f);
	for(register int i = hed[u];i;i = nxt[i]){
		register LL v = to[i];
		if(v == fa[u] || v == son[u]) continue;
		dfs2(v,v);
	}
}
//

//
inline void update_son(LL x,LL v){
	update(1,1,n,id[x],id[x] + siz[x] - 1,v);
}

inline LL query_son(LL x){
	return query(1,1,n,id[x],id[x] + siz[x] - 1);
}

inline void update_chain(LL x,LL y,LL v){
	while(top[x] != top[y]){
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		update(1,1,n,id[top[x]],id[x],v);
		x = fa[top[x]];
	}
	if(dep[x] > dep[y]) swap(x,y);
	update(1,1,n,id[x],id[y],v);
}

inline LL query_chain(LL x,LL y){
	register LL ans = 0;
	while(top[x] != top[y]){
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		ans += query(1,1,n,id[top[x]],id[x]);
		ans %= N;
		x = fa[top[x]];
	}
	if(dep[x] > dep[y]) swap(x,y);
	ans += query(1,1,n,id[x],id[y]);
	ans %= N;
	return ans;
}
//

int main(){
	register LL op,cz1,cz2,cz3;
	ios::sync_with_stdio(false);
	cin >> n >> q >> r >> N;
	for(register int i = 1;i <= n;i ++) cin >> w[i];
	for(register int i = 1;i < n;i ++){
		cin >> a >> b;
		add_edge(a,b);
		add_edge(b,a);
	}
	cnt = 0;
	dfs1(r,0);
	dfs2(r,r);
	build(1,1,n);
	while(q --){
		cin >> op;
		if(op == 1){ cin >> cz1 >> cz2 >> cz3; update_chain(cz1,cz2,cz3 % N); }
		if(op == 2){ cin >> cz1 >> cz2; cout << query_chain(cz1,cz2) % N << endl; }
		if(op == 3){ cin >> cz1 >> cz2; update_son(cz1,cz2 % N); }
		if(op == 4){ cin >> cz1; cout << query_son(cz1) % N << endl; }
	}
	return 0;
}

配合线段树 树链剖分还可以实现很多操作

此文章完结。感谢阅读。