IOI2020 国家集训队作业做题记录

也没做完，简单题都做掉之后，就做不下去了（（（

第一行是题目链接，第二行是 AC 代码评测记录链接。

rating 代表评定难度，enjoyment 代表做题体验，这两个都是个人主观评定的。

AGC035C

题
代码

有趣的构造。

这题是很久以前做的了。
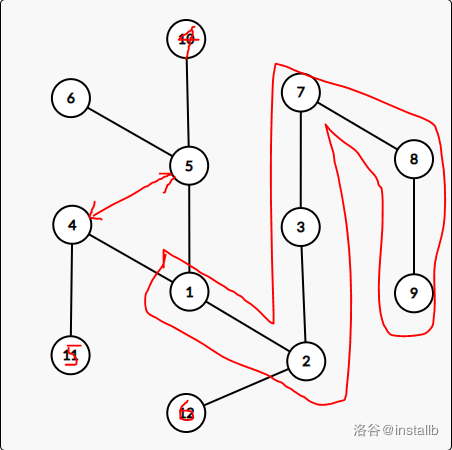
首先判无解，(2^k) 不可行，因为其它数异或不出最高位。

然后考虑把数一个个加上去，注意到 (2koplus(2k+1)=1)，所以把这两个数这样连到 (1) 上即可。

(2k)-(2k+1)-1-(2k)-(2k+1)

然后先把 (1) 到 (3) 对应的六个点连成一条链，其它的点直接这样挂在 (1) 上。

这样可以处理奇数了，但是还有偶数的情况，最大的那个莫得奇数和它配对了，这个数特殊处理一下，其实只要找两个数异或起来再异或 (1) 等于 (n) 就可以了，毕竟除了 (3) 每一个数都挂在 (1) 上了，我们只要找出两个数，分别对应 (n) 的最高位和去掉最高为后剩下的几位，找到 (k) 为不大于 (n) 的最大 (2) 的整数次幂，这两个数分别是 (koplus 1)（(k+1)） 和 (n-k)，这样不会涉及 (3) 的问题。

take (n=6) as an example：

CF527E

题
代码

这技巧挺神的。

先从单点考虑，如果一个点的度数为奇数，必定不行，所以先把度数为奇数的点两两连边。
再从整体考虑，这样还不一定足够，出入度都为偶数，代表出入度之和是 (4) 的倍数，那边数 ( imes 2) 必须是 (4) 的倍数，也就是边数必须为偶数。
边数是奇数的话，随便找个点加个自环就好了。

然后是找方案，这个比较有意思，我们发现加边后图中每一个点度数都是偶数，那么图中就存在欧拉回路了，而且是长度为偶数的欧拉回路（边数必为偶数）。把欧拉回路取出来，这么标边。

//起点和终点同一个点！
A<-B->C<-D->E<-F->(A)

经过一次一个点要么加 (2) 入度，要么加 (2) 出度。
重复经过一个点也无所谓，入度和出度还是必定为偶数的。

A<-B->C<-A->D<-E->(A)
A:2in 2out

AGC032C

题
代码

分类讨论题啊。

首先必须存在欧拉回路
然后如果存在点的度数 (geq 6) 则一定能分，由于存在欧拉回路，这个点可以分出去三个环，其它环可以直接拼上去。

如果所有点度数 (leq 2) 显然不行。

然后就是所有点度数 (=4) 了，如果这样的点有 (geq 3) 个，也能分出来。否则要分类讨论。

只有两个点度数为四只有两种可能，一种是中间拉四条链，另一种是两点各套一个环中间拉两条链，前者不行后者可以。

AGC030C

题
代码

神仙构造题。

至今不知道这题思路怎么想到的，自毙了。
有会的人能教教我吗

1 2 3 4 5 6
2 3 4 5 6 1
3 4 5 6 1 2
4 5 6 1 2 3
5 6 1 2 3 4
6 1 2 3 4 5

先这样，然后每一个数对应的对角线提出来，一个隔一个替换。

1 2 3 4 5 6
8 9 A B C 7
3 4 5 6 1 2
A B C 7 8 9
5 6 1 2 3 4
C 7 8 9 A B

AGC027D

题
代码

又是你，构造。

感觉比较无从下手，但是每一个格子只和上下左右的值之间的关系会影响结果，所有 (x+y) 为偶数（斜对角）的格子是互不影响的，我们可以先把这些互不影响的数确定下来，然后剩下的格子也是互不影响的，并且这些格子的值直接就确定了。

然后还要保证两两不同，
然后就是怎么保证不爆上界。

CF547E

题
代码

好像比较板子。

学了下 AC 自动机 fail 树 dfs 序建树状数组的操作。
SA 也能做，懒得写。

AGC034D

题
代码

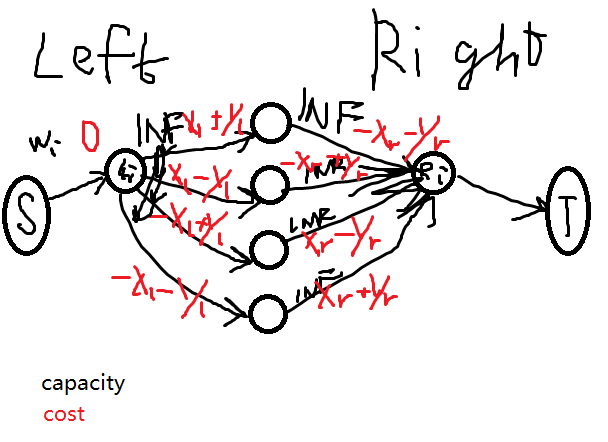
曼哈顿距离性质 + 费用流

一个简单思路就是每对红球蓝球连边，直接跑费用流，但是会 T。
这时候就发现题目里这个曼哈顿距离没有用到啊，这个肯定是有用的。考虑用到曼哈顿距离的一个性质
(dis_{i,j}=max((+x_i+y_i)+(-x_j-y_j),(+x_i-y_i)+(-x_j+y_j),(-x_i+y_i)+(+x_j-y_j),(-x_i-y_i)+(+x_j+y_j)))
于是中间加四个点，这样建图，要跑最大费用流，但其实可以直接转化过去，里面必有一个是最大值的相反数，所以最小费用流的相反数就是答案。
如果两两配对一定走的是四条中最长的路，也就是曼哈顿距离。

AGC037D

题
代码

没啥感受。

正推完全不会，于是看看能不能倒推，第三步可以给每一行排序，对最后应该在第 (i) 行的所有数染成颜色 (i)，第二步只要把颜色归位就行了，所以第一步操作后需要让每一列都有每种颜色的数各一个。
建二分图，左边行数，右边颜色，对每个数从它所在行连向它所在颜色，边代表取出一个这行这个颜色的数，取出一列就等价于取一个完美匹配（每行取一个，每种颜色取一个）。
把图建出来的话，每一个点的度数都为列数 (m)，每一次跑个完美匹配每个点度数 (-1)，左右点数一样并且每个点度数都一样，根据 Hall 定律，一定存在完美匹配，于是必定存在 (m) 个完美匹配。

AGC028C

题
代码

这题首先要切换角度，对着这个哈密顿回路瞪没啥用，我们考虑转化成每一个点的贡献。

我们任意挑选可行方案出来，发现每一个点 (u) （假设 (from) 连向它，它连向 (to)）的贡献只有四种情况：

• (a_u<b_{to},b_u<a_{from})，这个点选取 (a_u) 和 (b_u) 都计入答案。
• (a_u<b_{to},b_u>a_{from})，这个点选取 (a_u) 都计入答案。
• (a_u>b_{to},b_u<a_{from})，这个点选取 (b_u) 都计入答案。
• (a_u>b_{to},b_u>a_{from})，这个点 (a_u) 和 (b_u) 都不计入答案。

同时满足：

• 选取的数（(a) 被选的数量与 (b) 被选的数量之和）共计 (n) 个。

接下来我们从一个选取方案回推构图（哈密顿回路）方案。第一个想法是选取最小的 (n) 个数，但是这样是不对的，因为这样的选取方式不一定能对应一个方案。

我们看哈密顿回路中一条边的意义，为起点的 (a) 和终点的 (b) 选取较小的那个，这里我们可以采用一个技巧，把这个条件转化为起点的 (a) 和终点的 (b) 中选取且仅选取一个。

为什么这样正确？我们观察这样造成的多出来的一系列本应该不合法方案，发现如果这条边如果取另一个数答案一定更优，也就是说这些方案虽然不合法但是一定不能成为答案，所以，无所谓。

后面就简单了。

给出结论，只有这三种方案存在对应方案：

• 全选 (a)
• 全选 (b)
• 至少存在一个点 (a) 和 (b) 都被选择

前两种显然，不证了。

第三种口胡一下。
我们把左边那列视为 (a)，右边那列视为 (b)，选取的数为正方形，未选取的数为圆形。
我们要连 (n) 条边，连成一个环，一条边必须连接一个取和一个不取。

如果一部分选 (a)，一部分选 (b)，那么任意一个选 (a) 的点和任意一个选 (b) 的点是连不起来的，这个图不可能连通，所以不行。

如果有 (k) 个都选，必然也有 (k) 个都不选，这里再分四种情况：

• 全是都选或都不选

• 都选 + 只选 (a)

• 都选 + 只选 (b)
  和上一种本质一样。
  

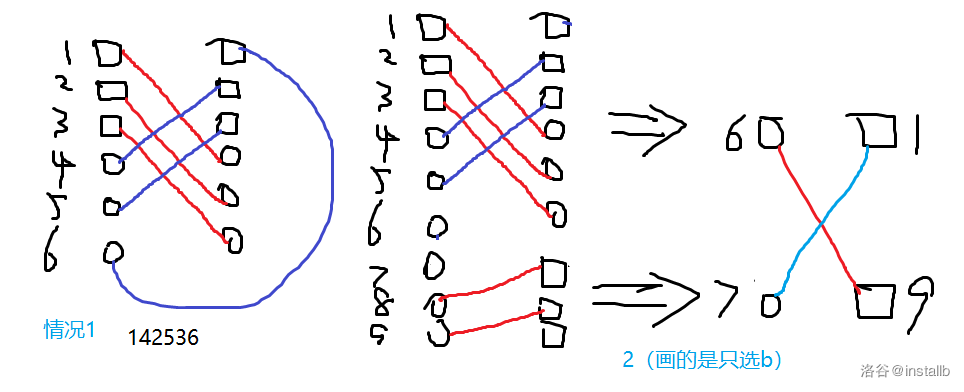
• 都选 + 只选 (a) + 只选 (b)
  

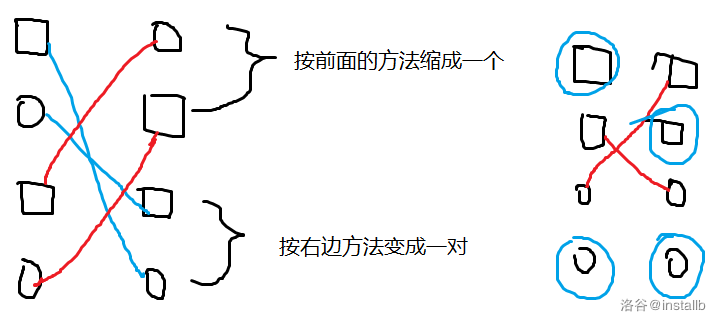
具体做法嘛。。前两个特判，后一种枚举一个强制两个都选，剩下所有数中的贪心选取最小的 (n-2) 个，因为其它点的选择是无所谓的。

这里先最小的 (n) 个全扔小根堆里，然后看每一个点强制双选的时候，它的 (a) 和 (b) 有几个数是在小根堆里，记为 (k)，(k) 只能是 (0) 或 (1) 或 (2)，用 (a) 和 (b) 中不在小根堆里的数之和加上小根堆中最小的 (n-k) 个数之和（这个可以预处理）更新答案。

ARC103D

题
代码

这题挺有意思。

这里我的方法和题解不一样，用的是三进制。
首先所有数 (x+y) 奇偶性相同不然无解。

把每个数用三进制表示，是三进制每一位用 (-1,0,1) 表示。
先从 (3^0) 到 (3^{18}) 每一个 (3^k) 写两个数，然后从低位往高摆，分情况。

• (x) 和 (y) 这一位都为 0
  LR/UD即可
• (x) 和 (y) 这一位都不为 0
  一个摆给 (x) 一个摆给 (y)
• (x) 和 (y) 其中一个为 0 一个不为 0
  把 1 变成 -2，然后进位，或者把 -1 变成 2，然后退位。

最后留下来最高位，如果 (x+y) 是奇数两数最高位之和必为奇数（前面所有的加起来是偶数，(3^{19}) 是奇数）再写一个 (3^{19})。如果 (x+y) 是偶数两数最高位之和必为偶数，再写两个 (3^{19})，按上面的方式凑就行了。

正好用满 40，正好卡满 (10^9)。

ARC093E

题
代码

用好 MST 的性质。

如果 (k) 比 MST 的权值大，那么图包含在任一 MST 里的边都必须染成一个颜色（这里有两种情况），不然就能选取某个最小生成树了，全部染成同一个颜色之后，最小的包含双色边的生成树一定与原图某个最生成树只相差一条边，否则其中一条必定可以被替换（只保留一个与 MST 颜色不同的边）。我们枚举替换的那条边 ((u,v))，还是考虑最小生成树的性质，只能替换掉原来 MST 中 (u) 和 (v) 之间路径上权值最大的边。如果替换完之后的生成树比 (k) 小（第一类边），那这条边必须和 MST 中所有边染同样的颜色，比 (k) 大（第二类边）则随便染什么颜色都行，等于 (k) 则把这些边都归到第三类。
第三类边必须存在，并且不能全部染成和 MST 同样的颜色，其它染色方案都行。

如果 (k) 和 MST 权值是一样的，原树 MST 就不一定能全染同色了，其实把所有包含在任一 MST 里的边当成第三类边就行了。注意这里算好以后要把第三类边数量减一，相当于先用一条边确定 MST 染什么颜色，再转化成上面的问题。

AGC024D

题
代码

神仙题，令人自闭。

首先找理论下界，由于只能加点不能删点，染色数是原图直径除以二上取整，对应直径中点到一端的所有点，因为对于这些点离该点最远的点到该点的距离 两两不同，以它们为根的树必不同构。

然后构造出理论下界对应的解。一种可能是把直径中点当根，我们要让深度相同的点都染上同样的颜色，每一个深度为 (i) 的点为根的子树必须完全相同，所以找到拥有深度为 (i+1) 的儿子最多的深度为 (i) 的点，首先要保证儿子节点数量相同，于是其它点都要加上对应的儿子数量，但这样还不行，因为这些儿子节点为根的子树也都必须长得一样，然后就得对 (i+1) 深度的点（包括新添加的节点）做一次一样的操作，一步步往下做。

还有另一种可能，可以看成是边当根，就是边所连的两个点深度为 0，然后处理它们的子树，这样也可能达成深度最大的点深度最小。

对应情况的答案就是每个深度儿子数量最多的点儿子数量相乘。

果然 n=2e5 是 sb 题，n=100 都是神题。

AGC032D

题
代码
这个做法应该比较简洁吧。

首先每一个数至多跑一次（从左往右或者从右往左或者不跑）因为如果让它跑两次相当于第一次就跑到第二次结束那地方就行，位置是可以任意选择的。

我们先假定左移和右移费用相同，然后把数分成两类，被移动了和未被移动。显然，未被移动的数必须构成一个上升子序列，那些移动的数分为三种情况，我们对每一个移动的数分别考虑，假设这个移动的数为第 (i) 个数 (a_i)。

先任意找一个可行方案（已经把所有数分为被移动和未被移动）出来。

• 1.未被移动的数中存在 (j)，(j<i) 且 (a_j>a_i)
  这个数应该往左移
• 2.未被移动的数中存在 (j)，(j>i) 且 (a_j<a_i)
  这个数应该往右移
  注意：由于子序列是上升的，上面两种情况不可能同时出现。
• 3.上两种情况均不出现
  这种情况在最优解种不可能出现，因为可以把这个数归到子序列里去，把它变成未被移动的数。

答案就是被移动的数的数量最小值乘以费用，前者等于总数减去最长上升子序列长度。

然后看左右移不同的情况，可以 dp 了，状态 (dp_i) 代表将第 (i) 个数选为未被移动的数，且前 (i) 个数能够构成上升子序列（也就是这些数都已经被决定是哪一类了）时，最小需要的总花费。

决策变量 (j) 枚举上一个处在上升子序列中的数是哪个，然后统计 (j) 和 (i) 中该左移和该右移的数分别有多少个。

对于这个统计，只要倒序枚举 (j)，两个变量就完事，左移的数看起来不好统计，其实只要把上文所述的第一种、第三种情况都当成左移的数就可以了，也就是 (a_k<a_i) 即左移 (k)。

AGC091F

题
代码
SG 函数打表找规律。

AGC029C

题
代码

好久不见二分答案了。

这题还是无从下手，然后意识到答案是单调的，于是可以先二分答案 (k)，然后发现如果 (S_{i-1}>S_{i})，那么第 (i) 个只要在第 (i-1) 个后面不停加 a 就行了。
剩下的按类似 (k) 进制的加法做（a 代表零），如果最高位（第 (1) 位）产生进位就不可行，由于 (S_{i-1}>S_{i})，第 (i) 个字符串前 (S_{i}) 位相当于第 (i-1) 位的前 (S_{i}) 位代表的数加上了 1，它之后的位全部清零，这个可以用一个按深度的单调栈存，加入的时候把比它低的位弹出来。

特判答案为 1。

CF555E

题
代码

简直板子题啊。

想一想如何构造方案？

点双缩点成树，同一个点双内一定有方案使得点能两两互达。
构造：dfs 树，树边父亲连到儿子，非树边（没有横叉边，所以都是儿子-祖先边）儿子连向祖先。

不同点双之间至多只有一条路径，点双缩点后构成森林，随便找个点当根，然后一条路径可以分为往上走和往下走两部分。

往上走那部分边打 1 标记，往下走那部分边打 2 标记，两个数组一遍树上差分统计每个边被打了几遍 1 和 2 标记，两者都不为零就直接无解，否则有解。

图不连通，硬加码量，坑人。

CF605E

题
代码

期望没好好学，难受。

用类似 Dijkstra 的思想贪心更新，首先 (n) 到 (n) 的最短路已经确定，然后每次找剩下未确定最短路的点中期望最小的那个点，把那个点确定下来，一个一个确定。

CF526F

题
代码

学到了个很强的做法，先膜拜 pinkrabbit。

首先每行每列只有一个，那就把它直接拍到一个序列上，记每一行的棋子的位置，记作 (a) 数组。

在这个数组里，还是右端点 (i) 从 (1) 开始往后扫，维护每一个的区间 ([j,i])，记录这个区间里有多少个数（即为 (num)），同时记录有多少个数 (k) 满足 (k) 和 (k+1) 都在这个区间内，记为 (cnt)，只要一个区间满足 (num = cnt + 1)，这个区间就满足条件。

用一个线段树维护对每一个下标 (j)，([j,i]) 的 (num-cnt)，右端点更新时，如果右端点的数为 (k)，那么假设数 (k-1) 出现在位置 $i $ 前的 (pos)，([1,pos]) 的 (cnt) 值加一，对 (k+1) 也这么做。然后 ([1,i]) 全部 (num) 加一。然后直接统计线段树最小值个数，因为一定有 (1) 而且没有更小的数。

ARC097F

题
代码

一个细节调一天系列。

首先如果一个叶子节点是黑色的，我们就不需要去经过那个点（当然这个点还是可以作为起点的）在树中删去这个点对答案没用影响，我们不断重复这个过程（删去一个点后可能有新的黑色叶子节点）。

然后得到一棵叶子节点都为白色的树，我们需要经过每一个叶子节点。这个路径比较难做，我们先考虑回路，也就是猫从 (u) 出发，遍历所有点后必须回到 (u)，这样一定是每条边正向反向各走一次，每一个点也由于进入这个点反转了这个点的度数次数次颜色，因此每一个点的最终颜色决定于它的入度和初始颜色数，前者等于删点后的树上这个点的度数。对翻转后还是白色的点做个标记，我们到达这些点的时候需要每个点额外翻转一次。

然后考虑从 (u) 到 (v) 的路径，我们发现这其实就是回路减去了这两点之间的所有边，相当于这中间的点除了 (u) 都少经过了一次，即经过恰好一次。

• 对于没被标记的点，少经过一次但同时要多翻转一次颜色。
• 对于标记了的点，少经过一次还少翻转一次颜色。

前者对答案的贡献为 (0)，后者对答案的贡献为 (-2)。
所以我们要找到一条路径，经过尽可能多的被标记了的点。

这不就是树的直径吗？
最后一个问题，这样 (u) 点本来不应该统计进去，答案不会多吗？
并不会！因为叶子节点的权值必定是 (0)，一定存在不包含叶子节点的直径，然后我们取叶子节点作为 (u)。

最后树形 DP 求直径，记得这里一定要找到一个没被删掉的点当根，再跑。

答案为删完剩余边数乘二加标记的点数减去直径长度。

ARC095F

题
代码

同构这个操作以前闻所未闻（除了这篇文章里另外一题）。

同构是个要求很高的东西，所有的能用序列生成的树应该是有一些性质的。

我们考虑按 (p_i) 从小到大一个一个加进去排列，同时构造树。
每次加入一个数 (i) 时，它连边只有两种情况，它在目前位置最靠后的数 (x) 的左边还是右边，前者不会改变 (x)，后者把 (x) 变为 (i)。这样把所有执行后者操作的点提出来是条链，前者就是点挂在链上。

树的性质是存在一条链，使得所有的点到这条链的距离 (leq 1)。

后面就好办了，把直径提取出来，把直径上点度数记录下来，看正着反着哪个字典序小，然后可以根据度数把排列构造出来了。

直径可以保证第一个点度数为 (1)，非直径不可以（否则这个链不满足那个性质了）

AGC034E

题
代码

AGC 最水 E 题

一开始没啥思路，先看数据范围吧，然后发现可以枚举移动到哪个点。

枚举根之后发现根确定了答案是确定的，就是所有点深度和除以二，如果深度和为奇数就不行，所以只要判断可行性。

于是枚举这个点，把它作为树的根，接下来就是每次选择两个有棋子的点，要求其中一个不能是另一个的祖先，各把这两个棋子移向父亲节点。但是这样还是很不可做，因为两个点可能在根的两个不同子树内，也可能是同一个。

自上而下不行，那么就自下而上考虑，把模型抽象一点，移向父亲就是深度减一，全部移到根就是所有点深度之和为零。我们可以计算出每一个子树内所有棋子深度之和的取值范围（这里计算子树时，考虑子树的根深度为零，向上转移时会考虑这一点），最大值即是所有点都不移动，最小值这里用到了一个贪心，这个取值其实是比较自由的，也算是用到了一个技巧，就是每次把所有子树的取值范围拿出来。最小值最大的取其最小值 (x)，其余的都取最大值，如果这样的情况下 (x) 比其它最大值之和 (sum) 还大，这个子树的最小值是 (x-sum)，否则只要所有数和为偶数，就是 (0)，因为必定能找出一种方案，使得所有数中，最大值小于等于所有数之和的一半，而这种情况下每次选两个数各减一，一定是可以减到 (0)。

如果所有数和为奇数，最小值就只能是 (1) 了。
不过子树里的 (1) 其实是不用管的，奇数当成最小值为 (0) 算甚至没有任何问题，只有根需要判，可以考虑一下上面的过程，确实是不需要。

最后如果根节点最小值为 (0)，那么符合条件，计算答案。

这题把一个最优化问题转化成了一个可行性问题。

CF521D

题
代码

调了好久，最后重构了一遍才过，自闭了。

看到赋值，加，乘，最后答案又是所有数乘积，可以想到如果确定了使用的操作是哪些，操作的顺序是先赋值再加最后乘，同一操作内部无所谓。然后赋值除了最大的那个也是没有用的。

考虑完这些还是不够，我们发现赋值由于只剩下一个了，又是先做的，可以把它直接转化成加操作。

这样只剩加和乘了，继续贪心，对于同一个数加肯定是先加大的再加小的，这个还是挺显然的，如果先选的小的，最后算答案把它替换成大的一定更优。然后就是比较不同数加与所有乘对答案的贡献了。我们可以把加也转化成乘，如果一个数是 (x)，加完后是 (x+y)，这个加操作对答案的贡献就是 ( imes frac{x+y}{x})，如果加的不是对应数最大，由于先加大的，加小的数时算 (x) 要把所有前面更大的大数视为已经选择并加上去了。

最后一个问题：赋值转成的加作为非最大值是否会有问题。其实不会，因为虽然选完之后要把赋值操作顺序提前，但是这些加操作对这个数的影响之和是一样的。

CF547D

题
代码
这题挺神的。

首先每行每列的点都是红蓝数相差至多 (1)，相当于奇数个点则相差 (1)，偶数个点必须数量相同。

把每行每列的点分别两两配对，两两配对的点颜色不同，就能满足条件。

但是这样需要图是二分图，不是这还是挺显然的，与一个点相连的两个点一定分别是与它同行和同列的各一个点，不可能两个都是同行或同列的，这样就不会有奇环了。

二分图染色。

ARC092D

题
代码

一开始做这题思路就错了，自闭了。

变向可以看作是删一条边 ((u,v)) 再加一条边 ((v,u))。
删边会发生什么？

• 1.什么都不发生
• 2.强连通分量数减少

加边会发生什么？

• 3.什么都不发生
• 4.强连通分量数增加

考虑 2 的条件，删边前 (v) 和 (u) 能够互达，删边后 (u) 不能到达 (v)。
考虑 4 的条件，加边前 (v) 不能到达 (u)，加边后 (u) 和 (v) 能够互达。

首先这两者肯定是不能同时发生的。

然后找切入点，如果删边前 (v) 和 (u) 能够互达，那么一定存在 (v) 到 (u) 的路径，从每个点出发搜一遍记录这个就可以了。

如果加边后 (u) 和 (v) 能够互达，那么除了 ((u,v)) 之外还存在一条 (u) 到 (v) 的路径，终点为 (v) 且中途不经过 (u) 和 (v)。这个比较难处理，如果 (u) 到 (v) 有两条路径的话，一条路径是直接 ((u,v)) 那么另一条路径是 (u) 先走到另一个点 (w) 再到 (x) 的，如果我们按 (u) 的所有出点的编号大小正序排序和倒序排序后的顺序，每次遍历这个出点能到哪些点的话，就可以保证如果 (u) 到 (v) 有两条路径，两次第一次遍历到 (v) 对应的出点编号是不同的，一个数不可能同时大于另一个数又小于这个数。具体实现其实只要用存边的顺序就可以了。

上面两点满足且满足一个就是 diff，如果都满足，那就存在一个环包含 (u) 和 (v) 且不包含边 ((u,v))，那么这条边就失去意义了，显然是 same。都不满足也是 same。

AGC030D

题
代码

一道挺神仙的 DP 题。

这种统计所有结果的逆序对之和肯定是没法直接做的，要转化问题（也算是常见技巧了把吧），我们把两者换一下，求每个逆序对在几种结果中是存在的，也就求 ((i,j)) 这对数在几个结果里满足这对数组成了逆序对。

这里每一步操作做或不做都会产生一种状态，于是再作一步转化，假设每一步操作都是 (frac{1}[2}) 概率做，(frac{1}[2}) 概率不做。最后每一种结果出现的概率为 (frac{1}{2^Q})。

考虑 DP，(dp_{i,j,k}) 表示前 (i) 个操作完成后，((j,k)) 能组成逆序对的概率。最后所有数对的概率乘上总方案数，求和即为答案。

AGC022E

题

CF576D

题
代码

不会 bitset 直接自闭。

按 (d_i) 的大小从小到大加入每一条边，先看这条边之前的所有边加入后，从 1 出发正好走 (d_i) 条能到达哪些点，然后加入这条边，直接 Floyd 任意两点最短路即可。
(O(n^3mlog d))（(n,m) 同阶），用 bitset 优化后 (O(frac{n^3mlog d}{w})) 可过。

AGC037E

题
代码

看到字典序最小，考虑贪心。
先看第一步翻转拼接以后的字符串，这里方便起见我们认为整个串中最小的字符是 a，其实也有可能不是，不过是一样的。在这个字符串中，如果接下来不再反转拼接，直接选取所有可截取的字符串中最小的那个。如果接下来会再反转拼接，我们要找出能使得 拼接后的字符串取出的最小字符串 最小 的字符串，观察翻转拼接的性质，字符串结尾如果有 (x) 个连续的 a，反转拼接后的字符串中间会有 (2x) 个连续的 a。这就是本题的切入点了，我们每一次反转拼接之后，可以将最长的连续的 a 的长度加倍，直到成为全 a 串为止。

我们要从第一步翻转拼接后的字符串里计算最长的连续的 a 的长度。

实现的时候可以直接找最小的字符串，然后把它的翻转接在前面，会比较好写。

CF704D

题
先全染贵的那个颜色，然后看最多能染几个便宜的颜色。
建二分图，左边行，右边列，加个上下界限制，最大流就是最多能染几个便宜的颜色。

最后建出来的图可以证明跑最大流是 (O(msqrt{n})) 的。

AGC020E

题
我是先想的如果没有 1 变 0 操作应该怎么做，明显是个区间 DP。
(f_{i,j}) 代表 ([i,j]) 方案数，(g_{i,j}) 代表缩成一个括号（以及只有一个字符的情况，0 或 1）(f) 转移的时候枚举最后一个括号位置。(g) 转移就枚举区间长度 (len) 的约数（(len) 除外）把这些缩成一个括号。

这题 (f) 还是一样的转移方式，不过算 (g) 的时候不同了，需要转移自的 (f) 需要是所有截取部分 AND 起来的值，可能会产生新的字符串，所以 DP 状态里就记字符串而不是区间了，记忆化搜索即可。

这个东西看起来复杂度很大但其实是对的，首先 (f) 刷出来的 (f) 不用考虑，因为 (f) 刷出来的 (f) 刷出来的 (f) 一定都是原来 (f) 的字串，还只有 (n) 个。而 (f) 也会产生 (g)，并且 (f) 的每一个子串都会产生一个 (g) 的计算，而 (g) 又会产生新的 (f)，这些产生出来的 (f) 是必须全部重新算的。

但是每次产生出来的 (f) 长度至多是原来 (g) 的一半，三次 (g) 产生 (f) 操作以后，长度就必定 (leq 13) 了。长度为 (n) 的 01串只有 (2^n) 个，当 (nleq 13) 的时候这其实并不大。

所以我们只需要考虑 (g) 变 (f) 一次和两次的情况就行了，而且分成 (f) 的次数两次乘起来还得小于 8，不然就长度太小了。其实最后生成的串可以看作是最早的原串取了几个字串拼起来的，这里用两次操作长度都减半举例好了。

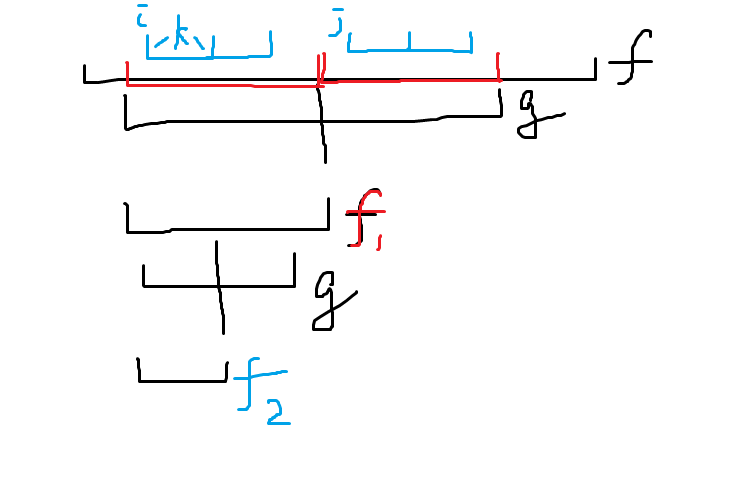
只用 (i,j,k) 就可以表示一个状态，那么状态数不会超过 (n^3)。
两次分别为分两段和分三段其实是一样的，状态数也只有 (n^3) 级别种。
实际值是远小于理论值的。

一共有 (n^3+2^{frac{n}{8}}) 个状态，转移用时 (n^2)，时间复杂度 (O(n^5+n^2 2^{frac{n}{8}}))

AGC020D

题

ARC101E

题

ARC101F

题
出口情况固定的机器人先扔掉，剩下的要么在左边的出口出要么在右边。
算出来到左右的距离，分别为 (x) 和 (y)，扔到坐标系上，找一条只往上或往右的折线，折线及其上方为从左边出，下方为右边出，(dp_i) 表示折线最后一个点经过的是 (i) 的总不同方案数，人为加上 ((0,0)) 和 ((inf,inf))。

CF590E

题
二合一了
前半部分直接跑 AC 自动机就 T 了，要只找到最近的有串的节点，然后一路路径压缩过去。
后面就是 DAG 最长反链

CF516D

题
这个 (f_x) 很奇怪，应该就是这题的切入点。
那个式子就是个尺取的形式吧，数据范围明示每次查询可以 (O(n)) 回答（不过实际上需要 dsu，多个 alpha）。　　

然后就是要加点删点维护最大连通块，但是这个 (f_x) 性质没用到，一般看到这种东西应该能想到和直径有关，这题把直径的重点当根，(f_x) 就是小根堆，证明也很显然，就因为到一个点最远的点必然是直径的两端之一。

这样加点用并查集合并，而删点可以直接删，当前连通块大小 -1 即可。因为不会把一个连通块分成两个了。

CF603E

题
首先那个点度数的条件一看就是要转化，保证在保存现有的边的情况下，每一个连通块大小都是偶数就可以了。如果不满足，可以删掉一些边，一定存在满足条件的方案。

用 LCT 维护最小生成森林，然后枚举现有的在森林中的最大边，能断则断，不能断更小的断掉也没意义。这个东西用堆维护就好了。

最后一步直接判最大值能不能删居然一直没想到，大概是遇到这种问题还没有这种意识。

CF685C

题

CF568C

题
一眼 2-SAT，字典序最小就贪心，然后全是细节。

根据贪心从左到右逐位考虑，虽然看起来后面对前面会有限制，但是通过 2-SAT 转成前面对后面的限制了。如果前面每一位都是顶上界的（和给定字符串相等）首选就是对应字符串的那一位，否则就是 'a'。

但这样很可能是不合法的，也就是说后面不管怎么填也没法合法，不过这个并不难判断，有以下两种情况，假设目前判断第 (i) 位能不能填给定字符。

• 前 (i) 位决定后，后面出现既必须为 'V' 又必须为 'C'
• 前 (i) 位决定后，前面仍然顶上界，假设第 (i+1) 到 (i+k) 位选 'C' 还是选 'V' 已经确定，而 (i+k+1) 位没确定或者这位已经是字符串以外的位置，并且这一段无论怎么选也选不出字典序比给定字符串那段大的字符串（比如 'V' 最大选 'b'，(i+1) 位只能选 'V'，而给定字符串要求 'c'）

第二种有点复杂

然后看最优情况下不行的话，还有什么选项可以填，会决定一个位置对后面是否有解的影响的，无非就两个。

• 前 (i) 位是否顶上界
• 第 (i) 位是 'C' 还是 'V'

四种情况枚举一下，即可，如果前面不顶上界了后面就不可能再顶了，注意字典序从小到大，我这里实现的比较复杂。

CF643G

题
神仙题。
从这题推广。
给出一堆数，令 (k= lfloorfrac{100}{p} floor) 每次删除 (k+1) 个两两不同的数，删到不能删为止，可以保证对的数不会被删掉。
然后把两堆删过的直接这样合并也是可以的（把一堆里的数一个个加入另一个）要考虑被加入的那堆里是不是已经存在那个数了。
既然区间可合并于是就可以线段树了...
区间赋值就打 tag + 对应那堆改成只剩一种数，次数是区间长度
存的时候存数值 + 处理后那堆还剩下这个数的出现次数
注意细节

CF639E

题
这个 (c) 明显提示二分答案了

最优顺序用邻项交换排序求出
令开始做 (i,j) 中先做的那个时已经用去了 (x) 时间。
令先做 (i) 更优，则有：

[p_i imes (1-frac{c(x+t_i)}{T})+p_j imes (1-frac{c(x+t_i+t_j)}{T})>p_i imes (1-frac{c(x+t_i)}{T})+p_j imes (1-frac{c(x+t_i+t_j)}{T}) ]

[xp_i+p_it_i+xp_j+p_jt_i+p_jt_j<xp_j+p_jt_j+xp_i+p_it_i+p_it_j ]

[p_jt_i<p_it_j ]

即 (frac{t_i}{p_i}<frac{t_j}{p_j})
对于 (frac{t_i}{p_i}) 相等的数可以随意交换，这样可以求出每个数最早和最晚可以放在哪个时间做完，这些数形成连续的一段，且段与段之间位置关系确定，第 (i) 个问题最早完成时间为这一段的起始时间加 (t_i)，最晚就是这个段的结束时间，即这个段的起始时间加这个段中所有问题用时之和，起始时间为这个段之前所有段用时之和。

如果两问题产生了 paradox，则同时满足两个条件：
(p_i<p_j)
(p_i imes(T-cx_i)>p_j imes(T-cx_j))
(x_i) 代表完成时间。
一定考虑最坏情况是否有 paradox，所以 (x_i) 取最小时间，(x_j) 取最大时间。
先按 (p_i) 排序，把第一个式子的影响去掉。然后保存所有 (p_k<p_i) 的 (p_k imes(T-cx_k)) 的最大值，做比较，即可。注意 (p) 是严格小于。

做这步的时候可以看出答案是有单调性的..

如果两问题处于同一段，也并不会有问题，因为在判断是否有 paradox 时，两数分别处于段的第一个和最后一个。

CF587D

题
首先看无解，如果一个点连了三个同色边肯定无解，如果有不止一种颜色有两条边连在这个点上，那么也无解。
这样每一个点最多存在一种颜色，有两条边连在了这个点上，把这个颜色找出来，用 2-SAT 两个边不同选加个限制。
然后一个点至多连一条边，可以用 2-SAT 前缀优化。
（xa_b 代表第 x_a 为 0/1，sa_b 代表前 a 个元素中是否有 1）

二分答案，有一些边直接强制不能选，然后跑 2-SAT。
2-SAT 强制选一个数或不选：连一条边 ( eg x o x) 或 (x o eg x)。

CF587F

题
AC 自动机 fail 树 dfs 序上建树状数组。
根号分治一下就好了。

CF585F

题
把 (s) 的长度 (geq lfloor frac{d}{2} floor) 的字串建出来，然后 AC 自动机上数位 dp。
找出第一次匹配上的位置，乘上剩下没填的位的方案数。最后加起来。

CF666E

题
离线，后缀数组 + 线段树合并（按 height 从小到大）
码码码

CF575A

题
首先考虑一步一步递推，当然会超时。
用矩阵加速，线段树维护矩阵区间乘积，从小到大依次处理每个特殊值，两个特殊值之间的部分可以加速，分类讨论一下。还需要快速幂。

这题没什么意思，就是码码码

CF571D

题
对两种集合分别建一个并查集，利用按 size 合并控制树高在 (log n) 级别，在 M 集每个点记录以这个点为根最后一次被清空的时间，每次清空都要找到根。
同时每次合并的时候要记录这个点是什么时候合并的，可以看作是记录在边上，因为会有合并之前有清空而合并后没有。

处理加操作更加复杂一点，需要每个点用一个 vector 记录操作，里面元素是按时间递增的。然后查询的时候先求出被查询的数最后一次被删除的时间，然后它的每一个祖先节点上二分查找即可。事实上只有一个点需要二分，比它更深的一定贡献为 0，比它更浅的一定所有操作都未被清空（不要忘记处理合并时间，同上）。

这里还会涉及到区间和，用前缀和就可以了，每次加入元素的时候也更新前缀和。

CF521E

题
显然三条路径在同一个边双联通分量中。先把割边都删掉，然后把每个连通块分别处理。把 dfs 树建出来。
最后有解肯定是长这个样子的
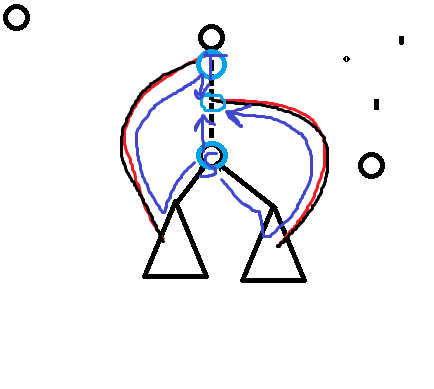
S 和 T 代表起点和终点

自下而上处理，每个点维护自己所在子树里能达到的深度最浅的点以及对应的那条返祖边（因为随着深度的上升，深度更深的点可能只能到达自己了，不能到达祖先，这样这条边就没用了，而最浅的那条边是最优情况）如果一个点 (u) 有两个或更多子树有返祖边可以到达这个点的祖先，则拿出来 (u) 和另外两个边连到的点（这两个可以是同一个点），就是图中的蓝点了。