(大量引用《2-SAT解法浅析 -by 华中师大一附中 赵爽》《由对称性解2-SAT问题》

在实际的题目中,限制往往还有除了或以外的别的形式,这些限制也将在这篇文章中讨论。
先讨论以下两类限制的情况:
1、若x=a,则y=b
2、x=a或y=b
由于x、y都是bool变量,值要么1,要么0,所以可以通过建有向图的方式来表示这个题目。对每个bool变量x,都建立两个点,分别表示x=1和x=0。为了方便,以后的x表示图中的一个点(除非x前加“变量”两字,表示变量),~x表示点x的对应点(即另一个表示同一变量的点)。图中有了点,就要考虑边了。
设X_a (字母大写以区分上文小写字母表示内容)为变量x等于一个数a对应的点。同时下文的‘^’表示异或符号。显然对上面的两类限制都可以通过连边实现:
对于第一种限制,要增这样两条边:(X_a,Y_b)即变量x=a可推出变量y=b;(Y_(b^1),X_(a^1))即变量y不等于b可推出变量x不等于a。
对于第二种限制,就要增这样两条边:(X_(a^1),Y_b)即变量x不等于a可推出变量y等于b;(Y_(b^1),X_a)即变量y不等于b可推出变量x不等于a。
发现这些边都是对称的,即若连了一条边(x,y),则必会有边(~y,~x)(注意这里的字母是小写的)在同一时间连上。同时也发现这些边的意义也很好理解,不就是“推出”嘛。并且每种限制所连的两条边都很好地将这个限制表示了出来。那么有了一个最基本的解决问题的暴力算法了:从每个变量x开始,若它有标记,则直接看下一个变量,否则枚举它选1或选0,设选了b,并从相应的点dfs。在dfs过程中标记遍历过的变量都选什么(对正向边则标记为该边的终点;反向边则标记为该边的对应点。是的,这个dfs也要走反向边,即一切有关系的都要走)。若发现dfs过程中遍历了一组对应点,即从当前变量x选b可推出某个变量既选1又选0,这显然是矛盾的,故当前变量不能选b,要选另一个。若当前变量选1或0都不行,则无解了(这里用不用让之前的变量重新选一下,再重新枚举当前变量的取值呢?答案是不用。因为若当前变量要取枚举取1取0,则当前变量肯定与之前变量关系。因为有关系的都被打上标记了。所以之前变量的取值情况是与当前变量独立的);否则就看下一个变量: 直到看完所有变量的值后发现仍没有矛盾,则每个变量枚举的值就是答案;或发现无解情况,就记录无解信息后停止就好。
显然这个算法是很慢的,时间复杂度可达O(n*m)。除非要求一个字典序最小的取值方案,否则一般都不用这个算法。下面介绍一个更快的算法:
我们考虑图的一个强连通分量。很明显,如果我们选中强连通分量中的任何一点,那么该强连通分量中的所有其它的顶点也必须被选择。所以我们可以先求图的所有强联通分量。当我们发现若一组对应点x和~x都在同一个强连通分量时,即若变量x选1,可推出它应该选0;它选0,可推出它应该选1,这样的话变量x不管怎么选都是矛盾的,则该2-sat无解。若没有这样的情况,那么我就叫他“前置合法”了,即已经满足了有解的前提之一。前置合法后,设原图为G,缩点后的图为G',然后,我们把G'中的所有弧反向,得到图G′′。由于已经进行了缩点的操作,因此G′′中一定不存在圈,也就是说,G''具有拓扑结构。我们把G中所有顶点置为“未着色”。按照拓扑顺序重复下面的操作:
1、选择第一个未着色的顶点u。把u染成红色。
2、把所有与u矛盾的顶点(如果存在x,~x∈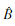 ,
,
前置合法时,k=1建的边不会影响强连通分量的对称性。(因为这条边的起点与终点不会在同一个强联通分量里)。
证明正确性前先了解几个定理:
1、
2、
3、
下面证明一下该算法的正确性:
一、
二、
1、
个人认为《2-SAT解法浅析》中有关二、1的证明是不正确的,这里可以举出一个反例:
所以下文给出作者个人的关于二、1的证明:
2、
故该算法是正确的。时间复杂度为O(n)(tarjan为O(n),拓扑排序为O(n),染色为O(n)(染色要注意不染重复的点,否则就可能变成O(n的平方))。故总复杂度也为O(n)(实际上,更准确的说,这里的n为n*2))
其实还有一个常数的优化:
故前置合法时必有解
故前置合法时,每个变量选他对应点中拓补序大的点,一定会得到一组解。这样的话就不用求完拓补序后再染色了。
再仔细考虑一下,发现tarjan的缩点的顺序正是一个反的拓补序,所以可以记录他tarjan的顺序,这样连拓扑序也不用求了。
代码