分治算法
一、大话分治
分治算法,Divide-and-Conquer Method,我给他它的字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。也正对应着它的单词Devide—分,Conquer—治。
分支思想是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
二、基本思想及策略实现
设计思想
将一个难以直接解决的大问题,分割成若干个不可再分割且相互独立的原子级问题,这些原子级问题与原问题形式相同并且可以直接求出解,然后把这些原子级问题各个击破,最后把所有原子级问题的解收集起来即原问题的解。
算法准备
分治法实际上就是类似于数学归纳法,找到解决本问题的求解方程公式,然后根据方程公式设计递归程序。
1、一定是先找到最小问题规模时的求解方法
2、然后考虑随着问题规模增大时的求解方法
3、找到求解的递归函数式后(各种规模或因子),设计递归程序即可。
分治的策略分为三步
1、Divide—分解:将原问题分解为若干个与原问题形式相同的子问题;
2、Conquer—解决:如果这些子问题可以直接解决,则解决并返回解,否则继续 分解;
3、Combine—合并:将各个子问题的解合并为原问题的解。
递归实现
分治算法的不断分解和收集解一般需要用递归实现,其实分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
三、分治法的应用场景
分治法所能解决的问题一般具有以下几个特征:
① 该问题可以分解为若干个规模较小的且相互对立的相同问题,即该问题具有最优子结构性质;(这是分治应用的前提)
② 该问题的规模缩小到一定的程度就可以容易地解决;
③ 利用该问题分解出的子问题的解可以合并为该问题的解;(这是分治算法的关键,如果不满足,则分治毫无意义。若果不满足这一条时,可考虑动态规划)
以下经典问题常用分治方法解决
(1)二分搜索
(2)大整数乘法
(3)Strassen矩阵乘法
(4)棋盘覆盖
(5)归并排序
(6)快速排序
(7)线性时间选择
(8)最接近点对问题
(9)循环赛日程表
(10)汉诺塔
四、分治法的具体实现
1、棋盘覆盖问题
问题描述:
在一个2^k×2^k 个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
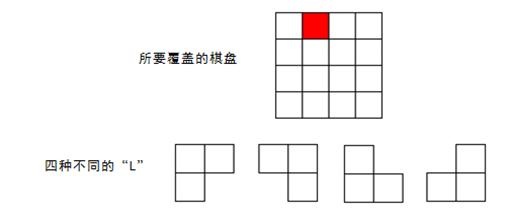
解题思路:
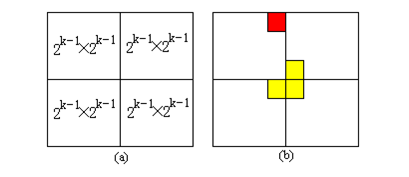
当k>0时,将2k×2k棋盘分割为4个2^k-1×2^k-1 子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1。
每次都对分割后的四个小方块进行判断,判断特殊方格是否在里面。这里的判断的方法是每次先记录下整个大方块的左上角(top left coner)方格的行列坐标,然后再与特殊方格坐标进行比较,就可以知道特殊方格是否在该块中。如果特殊方块在里面,这直接递归下去求即可,如果不在,这根据分割的四个方块的不同位置,把右下角、左下角、右上角或者左上角的方格标记为特殊方块,然后继续递归。在递归函数里,还要有一个变量s来记录边的方格数,每次对方块进行划分时,边的方格数都会减半,这个变量是为了方便判断特殊方格的位置。其次还要有一个变nCount来记录L型骨牌的数量。
Java代码实现
public class CoverChessBoard {
static int n=0;
static int k=4;
static int [][] board;
static int len=1;
{
while(k>0) {
len*=2;
k--;
}
board = new int[len][len];
}
//xy为当前数组起始坐标,len是当前块的长度,xs ys是标记点坐标
void cover(int x,int y,int len,int xs,int ys){
if(len == 1) return;
n++;
//定义中间坐标,方便运算
int xc=x+len/2-1,yc=y+len/2-1;
len/=2;
//标记点位于左上方区域
if(xs<=xc&&ys<=yc){
//先把其他三个区域的相邻角定点设为标记点并填充
//board[xc][yc]=n;
board[xc][yc+1] = n;
board[xc+1][yc] = n;
board[xc+1][yc+1] = n;
//把这个大区域分成四个相同大小的小区域,分别填充
cover(x,y,len,xs,ys);
cover(x,yc+1,len,xc,yc+1);
cover(xc+1,y,len,xc+1,yc);
cover(xc+1,yc+1,len,xc+1,yc+1);
}
//标记点位于右上区域
if(xs<=xc&&ys>yc){
//先把其他三个区域的相邻角定点设为标记点并填充
board[xc][yc]=n;
//board[xc][yc+1] = n;
board[xc+1][yc] = n;
board[xc+1][yc+1] = n;
//把这个大区域分成四个相同大小的小区域,分别填充
cover(x,y,len,xc,yc);
cover(x,yc+1,len,xs,ys);
cover(xc+1,y,len,xc+1,yc);
cover(xc+1,yc+1,len,xc+1,yc+1);
}
//标记点位于左下区域
if(xs>xc&&ys<=yc){
//先把其他三个区域的相邻角定点设为标记点并填充
board[xc][yc]=n;
board[xc][yc+1] = n;
//board[xc+1][yc] = n;
board[xc+1][yc+1] = n;
//把这个大区域分成四个相同大小的小区域,分别填充
cover(x,y,len,xc,yc);
cover(x,yc+1,len,xc,yc+1);
cover(xc+1,y,len,xs,ys);
cover(xc+1,yc+1,len,xc+1,yc+1);
}
//标记点位于右下区域
if(xs>xc&&ys>yc){
//先把其他三个区域的相邻角定点设为标记点并填充
board[xc][yc]=n;
board[xc][yc+1] = n;
board[xc+1][yc] = n;
//board[xc+1][yc+1] = n;
//把这个大区域分成四个相同大小的小区域,分别填充
cover(x,y,len,xc,yc);
cover(x,yc+1,len,xc,yc+1);
cover(xc+1,y,len,xc+1,yc);
cover(xc+1,yc+1,len,xs,ys);
}
}
public static void main(String[] args) {
CoverChessBoard cc = new CoverChessBoard();
System.out.println(len);
//数据测试,假设(10,10)是标记点
cc.cover(0, 0, len, 10, 10);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board.length; j++) {
if(cc.board[i][j]<10) System.out.print(0);
System.out.print(cc.board[i][j]+" ");
}System.out.println();
}
}
}
2、Strassen矩阵乘法
题目描述:矩阵m*n的A矩阵和n*p的B矩阵相乘,他们的乘积AB是个m*p的矩阵,求这个AB矩阵。
普通的暴力破解方法:直接通过三个for循环来模拟我们矩阵就算的过程,这样当然可以做出来,但是这样做的时候时间复杂度是O(n3),效率比较低。
Strassen矩阵乘法:
1969年,德国的一位数学家Strassen证明O(N^3)的解法并不是矩阵乘法的最优算法,他做了一系列工作使得最终的时间复杂度降低到了O(n^2.80)。他把矩阵分成多个块并定义了多个变量来便于计算,比如矩阵A={{a,b}{c,d}},矩阵B={{e,f}{g,h}},
那么两矩阵相乘的结果AB={{ae+bg,ag+bh}{ce+df,cg+dh}};
Strassen先生通过定义了7个变量来方便运算,变量如下
P1 = a ( f - h ) ;
P2 =(a + b ) h;
P3 = (c + d) e;
P4 = d (g - e );
P5 = ( a + d ) (e + h);
P6 = (b - d ) ( e + h);
P7 = (a - c) (e + f );
那么两矩阵乘积AB={{P5+P4-P2+P6 ,P1+P2} {P3+P4 ,P1+P5-P3-P7 }};
如此便完成了计算,如果我们我们遇到更大的矩阵时,我们先把矩阵等分成四部分,就比如是矩阵A中的a,b,c,d,按照Strassen方法模拟整个过程就可以实现了。因为只是个模拟的过程我就不在这里实现了。