向量
在编程上面,向量用(X,Y,Z)表示,也就是(123.156,194.156,215,00)
唉!那么和点的数据结构是一样的.
它表示(0,0,0)到(X,Y,Z)的方向和大小(长度).
它主要的目的是累加方向,也就是如果你从a点到b点,又从b到某个方向的时候可以用它.
而单位向量是什么?
可以看下面点乘中的 public static Point3d GetNormal(this Point3d ob_vector) 了解得知 :)
那么两个点怎么转换成向量呢?
数学上就是b点-a点=(x2-x1,y2-y1,z2-z1),而cad提供了一个方法b.GetVectorTo(a).
点乘的意义
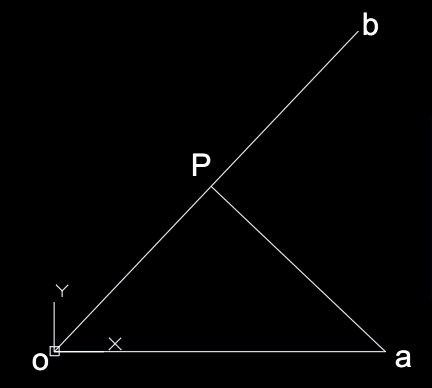
下图所示,oa是向量,ob是向量,求op的距离和p点坐标.
现象就是a点投影到P点上,会呈现一个90度直角...而且oa实际上是任意的,不需要和x轴重合(带角度也可以).
虽然说B站有视频教程,但是直接看代码貌似理解更方便...
代码:
/// <summary> /// 点积,求投影长度 /// </summary> /// <param name="o">原点</param> /// <param name="a"></param> /// <param name="b"></param> /// <returns>长度</returns> public static double DotProductLength(Point3d o, Point3d a, Point3d b) { var oa_vector = o.GetVectorTo(a); var ob_vector = o.GetVectorTo(b); //单位向量,cad自带的 Vector3d ob_UnitVector = ob_vector.GetNormal(); //求得op长度 var op_length = oa_vector.DotProduct(ob_UnitVector);//点乘,=(v1.X * v2.X) + (v1.Y * v2.Y) + (v1.Z * v2.Z); return op_length; } /// <summary> /// 点积,求投影坐标 /// </summary> /// <param name="o">原点</param> /// <param name="a"></param> /// <param name="b"></param> /// <returns>坐标点</returns> public static Vector3d DotProduct(Point3d o, Point3d a, Point3d b) { //点乘就是将oa向量投影到ob向量上面 //单位向量,cad自带的 Vector3d ob_UnitVector = o.GetVectorTo(b).GetNormal(); //求得op坐标(也就是呈现90度角的坐标) //如果O不在坐标原点,需要平移,那么最终P的最终坐标 = O的坐标 + 求出来的P的坐标 Vector3d v = ob_UnitVector * DotProductLength(o,a,b); //从0,0再平移回去 return new Vector3d(v.X + o.X, v.Y + o.Y, v.Z + o.Z); } /// <summary> /// 获取单位向量,仿照向量的GetNormal的数学实现,了解原理,用了Point3d代替向量 /// </summary> /// <param name="ob_vector"></param> /// <returns></returns> public static Point3d GetNormal(this Point3d ob_vector) { //https://www.bilibili.com/video/BV1qb411M7wL?from=search&seid=9280697047969917119 #if true //向量模长(也就是长度) var ob_length = Point3d.Origin.DistanceTo(ob_vector); #else //两点的距离 //向量模长数学版 √(x²+y²+z²) var ob_length = Sqrt(ob_vector.X * ob_vector.X + ob_vector.Y * ob_vector.Y + ob_vector.Z * ob_vector.Z); #endif //单位向量数学版 (x/ob_length,y/ob_length,z/ob_length) return ob_vector / ob_length; }
测试代码:

/// <summary> /// 测试点乘代码,点1=o,点2=a,点3=b /// </summary> [CommandMethod("tete")] public void tete() { var dm = Acap.DocumentManager; Editor ed = dm.MdiActiveDocument.Editor; var options = new PromptPointOptions(" 点位置:"); var pts = new List<Point3d>(); for (int i = 0; i < 3; i++) { var pot = ed.GetPoint(options); if (pot.Status != PromptStatus.OK) { return; } pts.Add(pot.Value); } var length = DotProduct(pts[0], pts[1], pts[2]); ed.WriteMessage(" op长度是:" + length); var ss = CrossNormal(Vector3d.XAxis, Vector3d.YAxis); ed.WriteMessage(" 叉乘向量是:" + ss); }
再深入,通过AB和C求E点,就是 E == AC点乘AB

叉乘的意义
叉乘有三个意义:
二维叉乘:
A:返回值是数值,有正负,表示绕原点四象限的位置变换,也就是有向面积,面积属性可以用来求解凸包的单峰函数....知道有这个意义就好....
B:返回值是数值,有正负,如果大于0表示顺时针.
三维叉乘:
A:返回值是向量.例如X轴叉乘Y轴表示Z轴,
如果叉乘的不是XY轴,而是两个三维向量(并不需要90度),那么就可以求出一个平面的法向量.
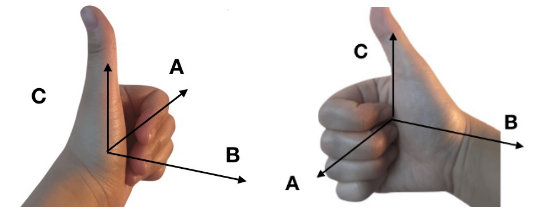
(左手叉乘) (右手叉乘)
同样的A叉乘B,左右手叉乘的方式刚好方向相反.图来自
必要的 视频参考
左右手坐标系相互转换:
如果将左a重合到右a,将左b重合到右b,那么左c和右c的关系刚好是正负的关系,结果*-1即可将左c变成右c.
/// <summary> /// 叉积,二维叉乘计算 /// </summary> /// <param name="a">传参是向量,表示原点是0,0</param> /// <param name="b">传参是向量,表示原点是0,0</param> /// <returns>其模为a与b构成的平行四边形面积</returns> public static double Cross(Vector2d a, Vector2d b) { // 抛出向量的思想,正常求平行四边形面积本来就是底乘以高 // https://www.zhihu.com/question/22902370 return a.X * b.Y - a.Y * b.X; } // 判断点在三角形内部 https://blog.csdn.net/pdcxs007/article/details/51436483 // 视频,右手螺旋法则 https://www.bilibili.com/video/BV1S741157cb?from=search&seid=1379331852253162293 /// <summary> /// 叉积,二维叉乘计算 |p1 p2| X |p1 p| /// </summary> /// <param name="a">传参是点,表示原点为此</param> /// <param name="b">传参是点,表示以a到b组成向量</param> /// <param name="n">传参是点,表示以a到n组成向量,此为判断点</param> /// <returns>返回值有正负,表示绕原点四象限的位置变换,也就是有向面积</returns> public static double Cross(Point2d a, Point2d b, Point2d n) { //这样计算没有保证原点. //三种计算是一样的,本质是矩阵,和传参顺序的问题 //return (b.X - a.X) * (n.Y - a.Y) - (n.X - a.X) * (b.Y - a.Y); //return (a.X - b.X) * (a.Y - n.Y) - (a.X - n.X) * (a.Y - b.Y); return (a.X - n.X) * (b.Y - n.Y) - (b.X - n.X) * (a.Y - n.Y); } /// <summary> /// 叉积,顺时针方向为真 /// </summary> /// <param name="a">直线点1</param> /// <param name="b">直线点2</param> /// <param name="n">判断点</param> /// <returns>返回值表示n点在ab向量的顺时针方向</returns> public static bool CrossClockwise(Point2d a, Point2d b, Point2d n) { return Cross(a, b, n) > -1e-6; } /// <summary> /// 叉积,求出法向量,三维叉乘(X轴*Y轴==Z轴) /// </summary> /// <param name="a">向量a</param> /// <param name="b">向量b</param> /// <returns>返回值是一个向量,X*Y表示Z或者-Z,正负是左右手坐标系</returns> public static Vector3d CrossNormal(Vector3d a, Vector3d b) { //y1*z2-y2*z1,z1*x2-z2*x1,x1*y2-x2*y1 return new Vector3d(a.Y * b.Z - b.Y * a.Z, a.Z * b.X - b.Z * a.X, a.X * b.Y - b.X * a.Y); }
(完)
