1 多元线性回归假设形式
多元线性回归算法的假设函数：
矩阵表示形式：
其中，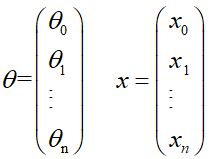
2 多元梯度下降
梯度下降算法：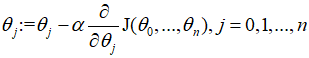
将成本函数代入得：
3 特征缩放
为了使梯度下降算法更快的收敛，我们可以使用特征缩放将每一个特征值（元/属性）限定到[-1,1]的范围。经验值是不得大于[-3,3]，不得小于[-1/3,1/3]。
均值归一化：可以利用公式
；来缩放特征，其中
是特征值，
是该特征值的均值，
是该特征值的范围或者方差
4 学习速率
如何保证梯度下降算法的正常运行？
如何选择合适的学习速率α？
画出J(θ)为纵坐标，迭代步数为横坐标的曲线。如果曲线不是单调减函数，一般来说，是α太大的原因，试试更小的α即可。
α的选择经验是...,0.001,0.003,0.01,0.03,0.1,0.3,1,3,...
5 特征的选择
有时候将所有的特征直接应用到数据上效果会不太理想，根据现实情况，将某些特征值做一些运算合并成一个特征会取得更好的效果。
有时候，数据的分布并不是线性的，此时可以用多项式回归，将一个多项式，如二次函数或三次函数拟合到数据上。
6 标准方程
求θ，使得J(θ)最小。梯度下降是一种迭代算法，而标准方程法是解析解法。
原理：对所有的θ求偏导，然后令其等于零。
，其中X为设计矩阵
,
,
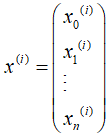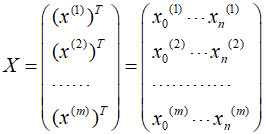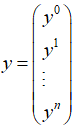
注意：使用标准方程法不需要进行特征归一化
优点：
- 不需要选择学习速率；
- 不需要迭代
缺点：
- 需要计算
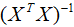，时间复杂度接近O(n3)。当特征数量比较大时，计算耗时会很大。一般，当n>>10000时，选择梯度下降算法。 - 适用模型有限，在线性回归模型中可以作为梯度下降的更优的替代算法。