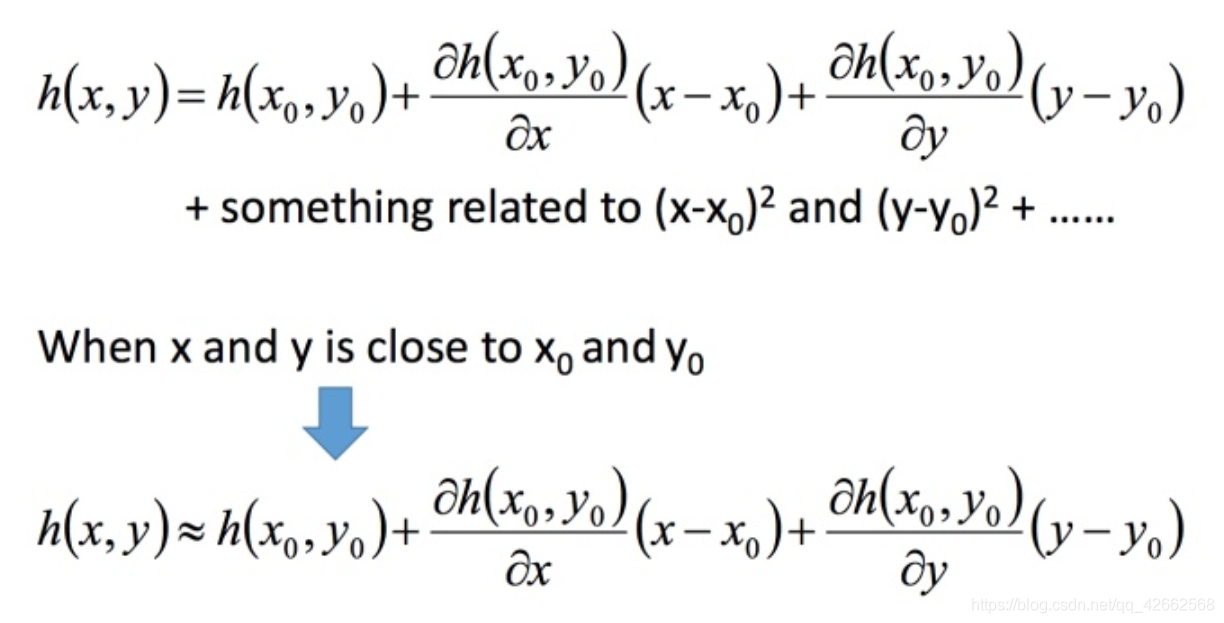Task06——梯度下降
导数我们都非常熟悉,既可以表示某点的切线斜率,也可以表示某点变化率,公式如下表示:f ′ ( x ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x f^{prime}(x)=lim _{Delta x
ightarrow 0} frac{Delta y}{Delta x}=lim _{Delta x
ightarrow 0} frac{f(x+Delta x)-f(x)}{Delta x} f ′ ( x ) = lim Δ x → 0 Δ x Δ y = lim Δ x → 0 Δ x f ( x + Δ x ) − f ( x ) f x ( x , y ) f_{x}(x, y) f x ( x , y ) y y y f ( x , y ) f(x,y) f ( x , y ) x x x f y ( x , y ) f_{y}(x, y) f y ( x , y ) x x x f ( x , y ) f(x,y) f ( x , y ) y y y x x x y y y f ( x , y ) f(x,y) f ( x , y ) u = cos θ i + sin θ j u=cos heta i+sin heta j u = cos θ i + sin θ j lim t → 0 f ( x + t cos θ , y + t sin θ ) − f ( x ) t lim _{t
ightarrow 0} frac{f(x+t cos heta, y+t sin heta)-f(x)}{t} lim t → 0 t f ( x + t cos θ , y + t sin θ ) − f ( x ) D u f D_{u}f D u f D u f = f x ( x , y ) cos θ + f y ( x , y ) sin θ = [ f x ( x , y ) f y ( x , y ) ] [ cos θ sin θ ] D_{u} f=f_{x}(x, y) cos heta+f_{y}(x, y) sin heta=left[f_{x}(x, y) quad f_{y}(x, y)
ight]left[�egin{array}{c}{cos heta} \ {sin heta}end{array}
ight] D u f = f x ( x , y ) cos θ + f y ( x , y ) sin θ = [ f x ( x , y ) f y ( x , y ) ] [ cos θ sin θ ] D u f = A × I = ∣ A ∣ ∣ I ∣ cos α D_{u} f=mathbf{A} imes mathbf{I}=|mathbf{A}||mathbf{I}| cos alpha D u f = A × I = ∣ A ∣ ∣ I ∣ cos α α alpha α α alpha α D u f D_{u}f D u f f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_{0},y_{0}) ( x 0 , y 0 ) [ ∂ f ∂ x 0 ∂ f ∂ y 0 ] left[�egin{array}{c}{frac{partial f}{partial x_{0}}} \ {frac{partial f}{partial y_{0}}}end{array}
ight] [ ∂ x 0 ∂ f ∂ y 0 ∂ f ] f ( x , y ) f(x,y) f ( x , y ) 沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向(去负号),则就是更加容易找到函数的最小值。
在回归问题的第三步中,需要解决下面的最优化问题:
θ ∗ = arg min θ L ( θ ) (1) heta^∗= underset{ heta }{operatorname{arg min}} L( heta) ag1 θ ∗ = θ a r g m i n L ( θ ) ( 1 )
L L L θ heta θ
这里的parameters是复数,即 θ heta θ w w w b b b
我们要找一组参数 θ heta θ
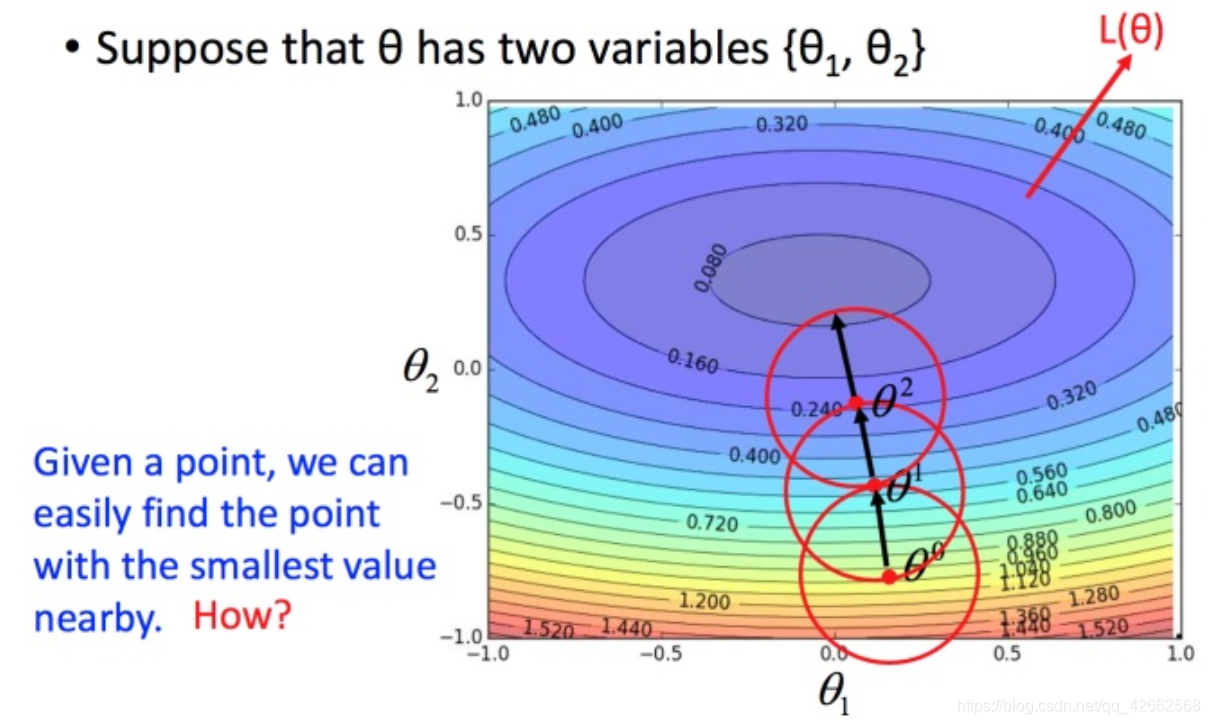
假设 θ heta θ θ 1 , θ 2 heta_1, heta_2 θ 1 , θ 2
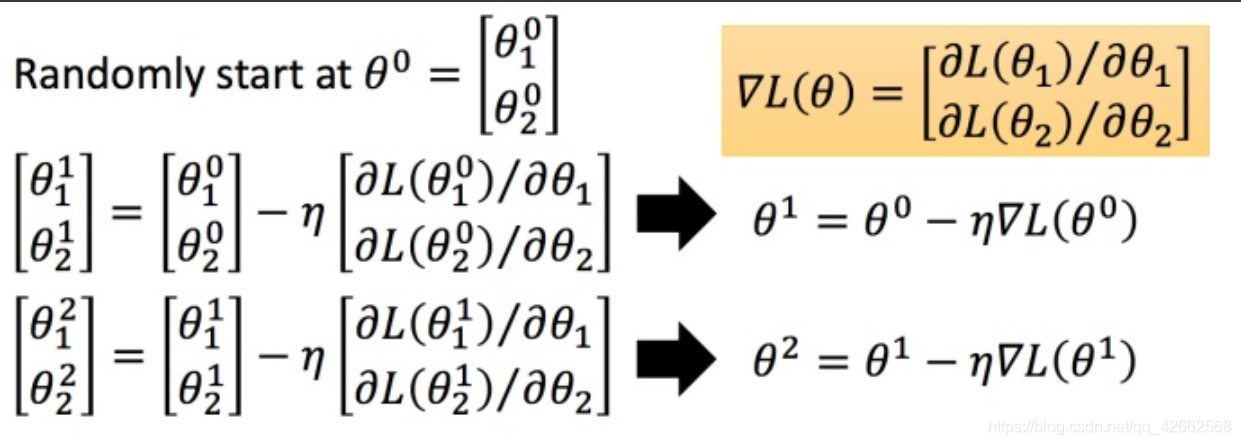
θ 0 = [ θ 1 0 θ 2 0 ] (2)
heta^0 = �egin{bmatrix}
heta_1^0 \
heta_2^0
end{bmatrix} ag2
θ 0 = [ θ 1 0 θ 2 0 ] ( 2 )
这里可能某个平台不支持矩阵输入,看下图就好。
然后分别计算初始点处,两个参数对 L L L θ 0 heta^0 θ 0 η eta η ▽ L ( θ ) riangledown L( heta) ▽ L ( θ )
η eta η
上图举例将梯度下降法的计算过程进行可视化。
举例:
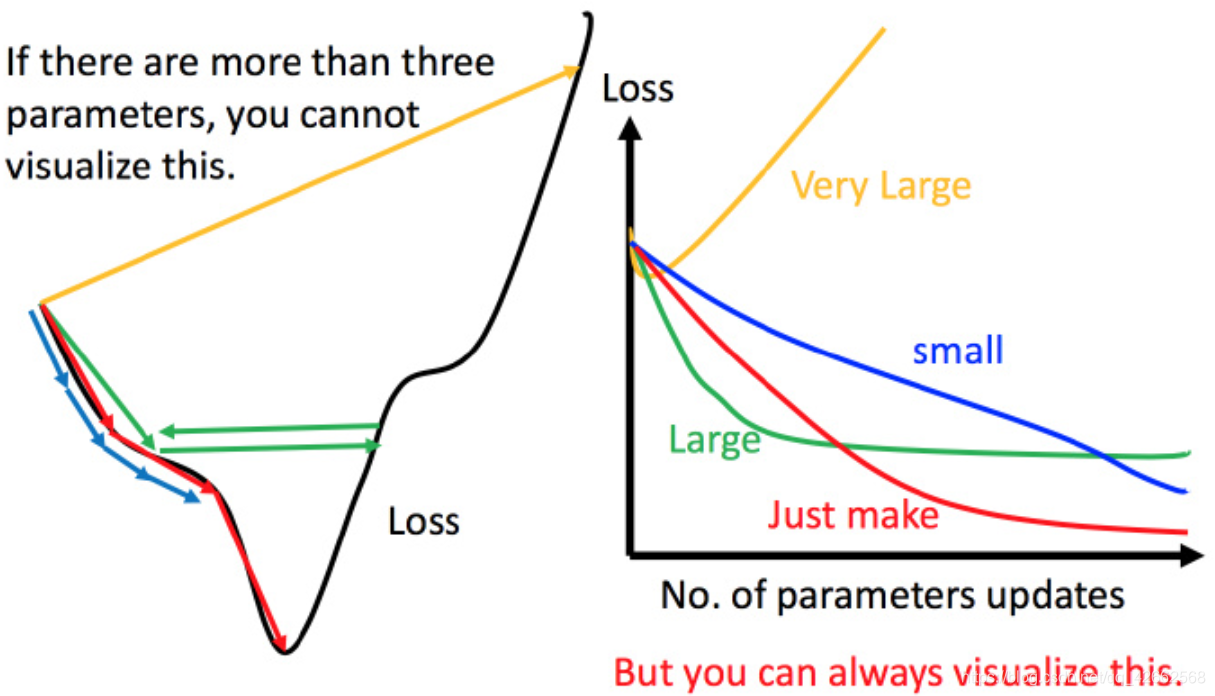
上图左边黑色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
update好几次参数之后呢,比较靠近最低点了,此时减少学习率
比如 η t = η t t + 1 eta^t =frac{eta^t}{sqrt{t+1}} η t = t + 1 η t t t t η t eta^t η t
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
每个参数的学习率都把它除上之前微分的均方根。解释:
普通的梯度下降为:
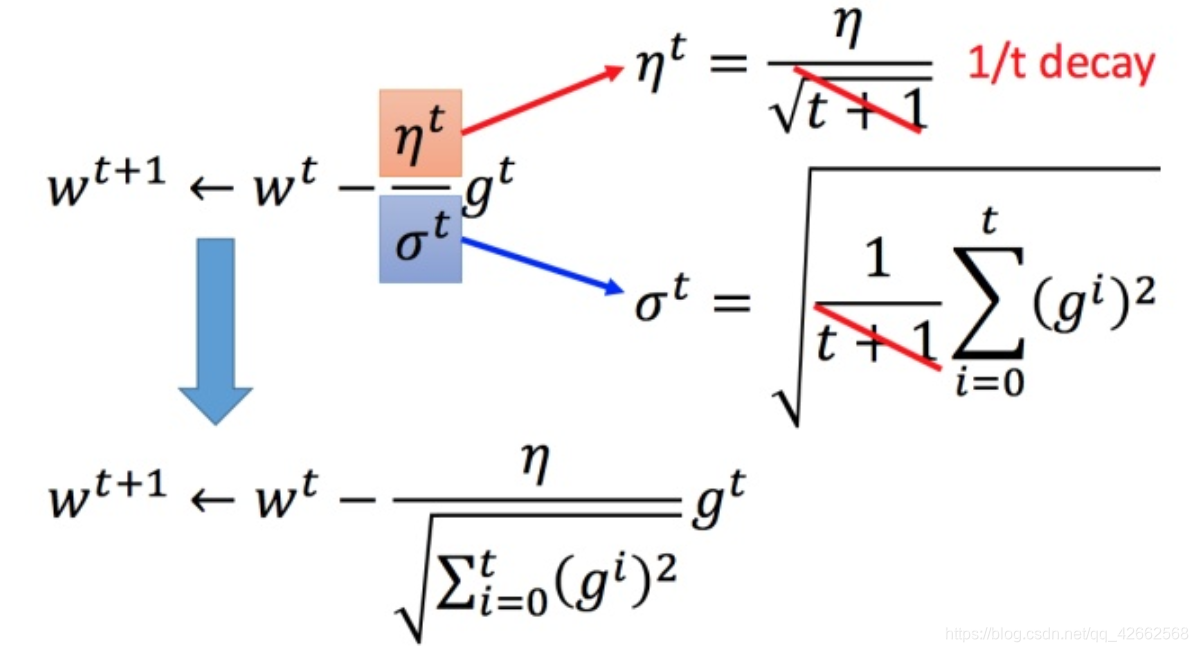
w t + 1 ← w t − η t g t (3) w^{t+1} leftarrow w^t -η^tg^t ag3 w t + 1 ← w t − η t g t ( 3 ) η t = η t t + 1 (4) eta^t =frac{eta^t}{sqrt{t+1}} ag4 η t = t + 1 η t ( 4 )
Adagrad 可以做的更好:w t + 1 ← w t − η t σ t g t (5) w^{t+1} leftarrow w^t -frac{η^t}{sigma^t}g^t ag5 w t + 1 ← w t − σ t η t g t ( 5 ) g t = ∂ L ( θ t ) ∂ w (6) g^t =frac{partial L( heta^t)}{partial w} ag6 g t = ∂ w ∂ L ( θ t ) ( 6 )
σ t sigma^t σ t
下图是一个参数的更新过程
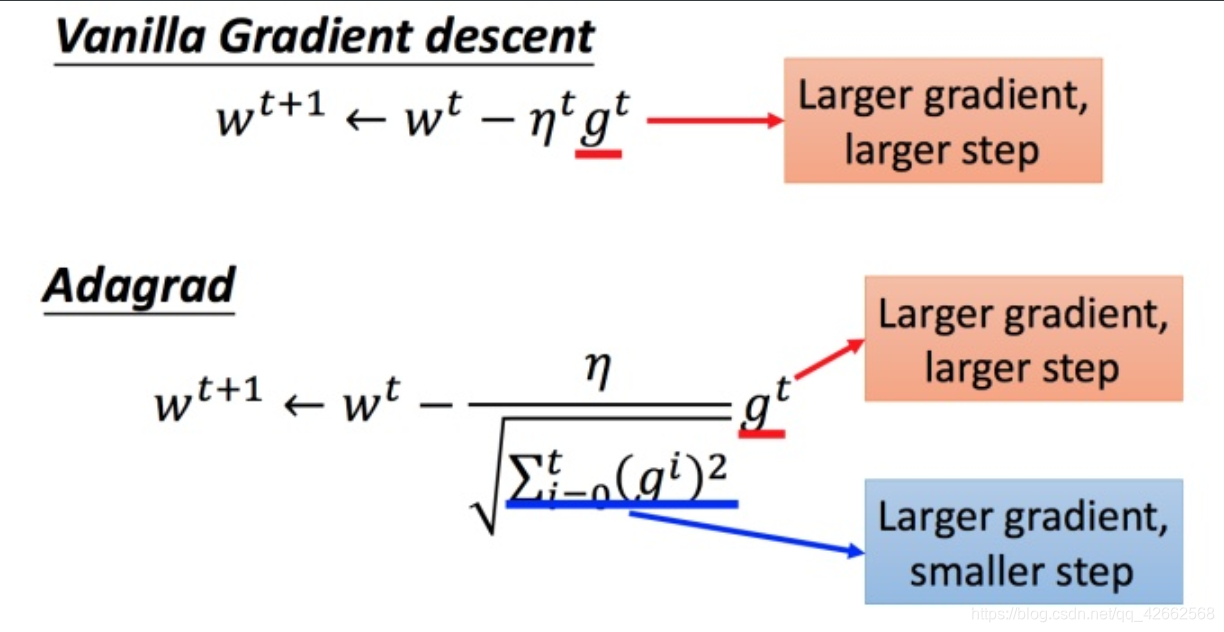
在 Adagrad 中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。
下图是一个直观的解释:
下面给一个正式的解释:
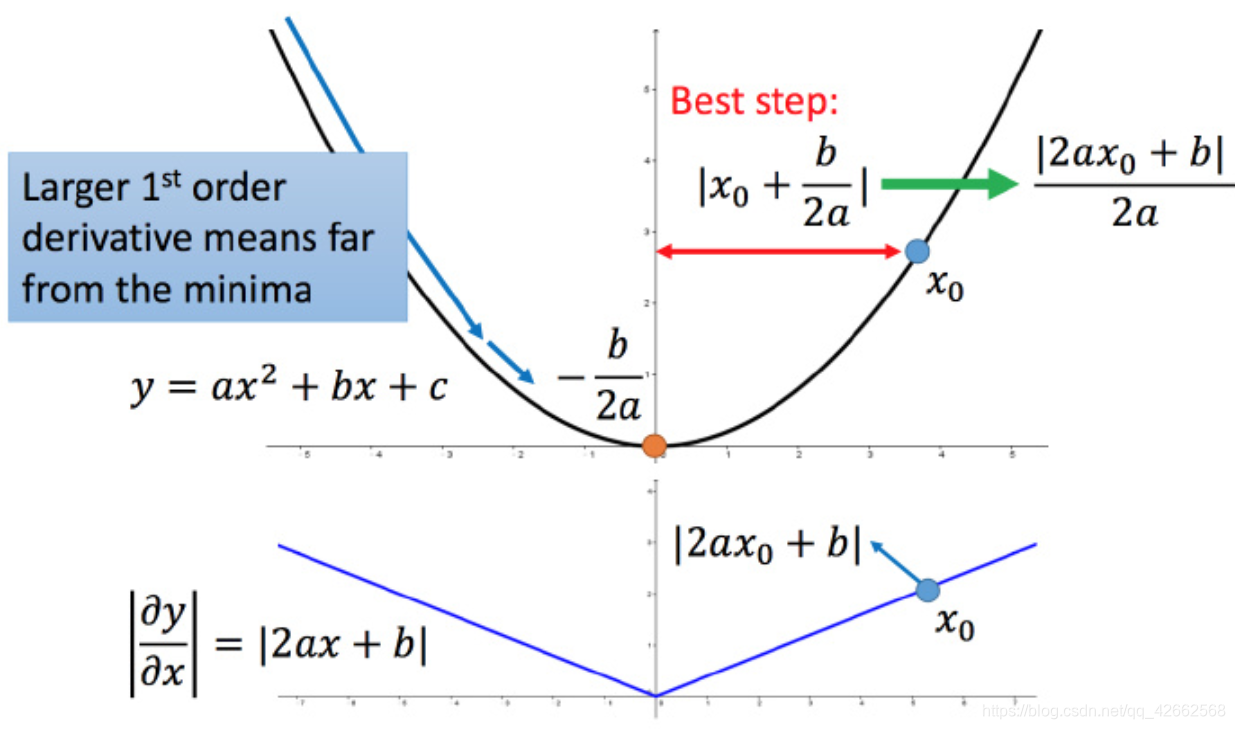
比如初始点在 x 0 x_0 x 0 − b 2 a −frac{b}{2a} − 2 a b x 0 x0 x 0 ∣ x 0 + b 2 a ∣ left | x_0+frac{b}{2a}
ight | ∣ ∣ x 0 + 2 a b ∣ ∣ ∣ 2 a x 0 + b 2 a ∣ left | frac{2ax_0+b}{2a}
ight | ∣ ∣ 2 a 2 a x 0 + b ∣ ∣ ∣ 2 a x 0 + b ∣ |2ax_0+b| ∣ 2 a x 0 + b ∣ x 0 x_0 x 0
这样可以认为如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
结论1-1:梯度越大,就跟最低点的距离越远。
这个结论在多个参数的时候就不一定成立了。
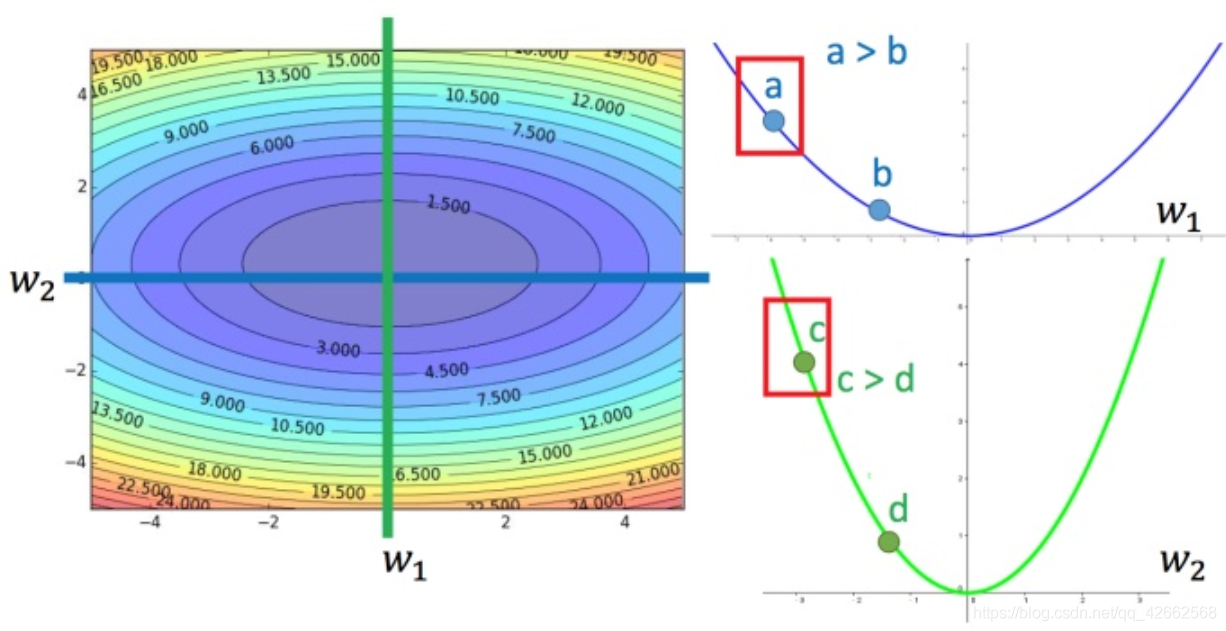
对比不同的参数
上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w 1 w_1 w 1 w 2 w_2 w 2 a a a b b b c c c b b b a a a c c c c c c a a a c c c
所以结论1-1是在没有考虑跨参数对比的情况下,才能成立的。所以还不完善。
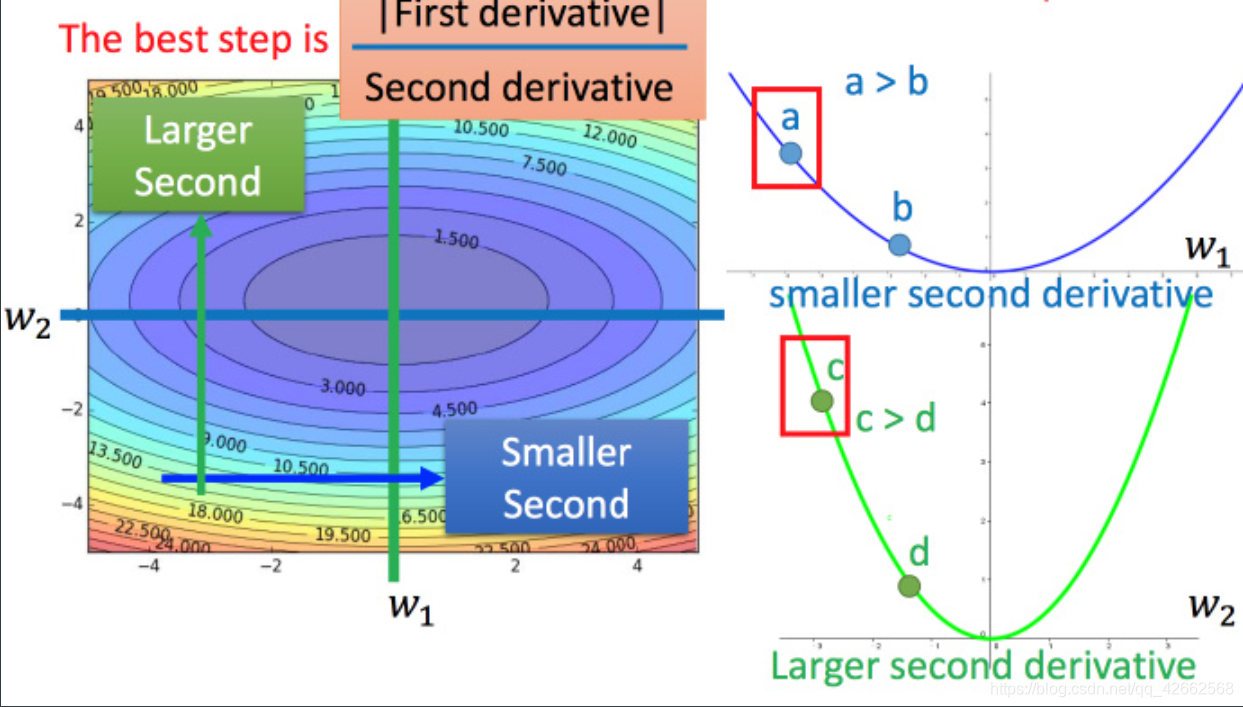
之前说到的最佳距离 ∣ 2 a x 0 + b 2 a ∣ left | frac{2ax_0+b}{2a}
ight | ∣ ∣ 2 a 2 a x 0 + b ∣ ∣ 2 a 2a 2 a ∂ 2 y ∂ x 2 = 2 a (7) frac{partial ^2y}{partial x^2} = 2a ag7 ∂ x 2 ∂ 2 y = 2 a ( 7 ) 一 次 微 分 二 次 微 分 frac{一次微分}{二次微分} 二 次 微 分 一 次 微 分
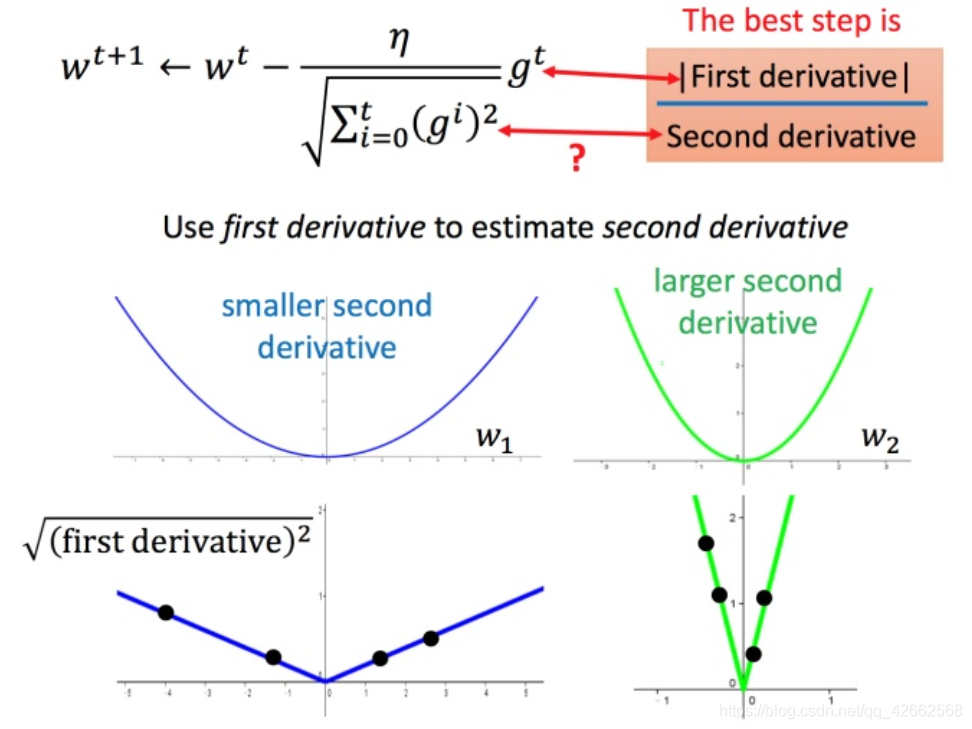
再回到之前的 Adagrad
对于 ∑ i = 0 t ( g i ) 2 sqrt{sum_{i=0}^t(g^i)^2} ∑ i = 0 t ( g i ) 2
之前的梯度下降:
L = ∑ n ( y ^ n − ( b + ∑ w i x i n ) ) 2 (8) L=sum_n(hat y^n-(b+sum w_ix_i^n))^2 ag8 L = n ∑ ( y ^ n − ( b + ∑ w i x i n ) ) 2 ( 8 ) θ i = θ i − 1 − η ▽ L ( θ i − 1 ) (9) heta^i = heta^{i-1}- eta riangledown L( heta^{i-1}) ag9 θ i = θ i − 1 − η ▽ L ( θ i − 1 ) ( 9 )
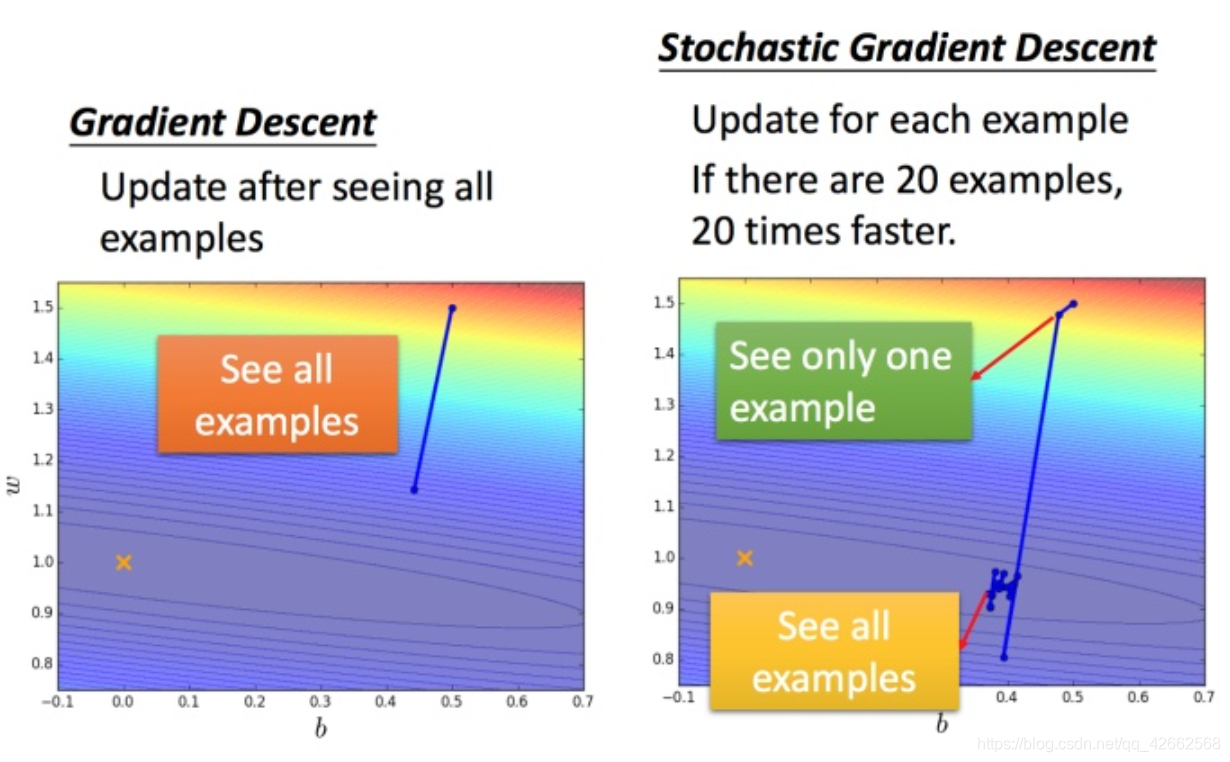
而随机梯度下降法更快:
损失函数不需要处理训练集所有的数据,选取一个例子 x n x^n x n
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 (10) L=(hat y^n-(b+sum w_ix_i^n))^2 ag{10} L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 ( 1 0 ) θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) (11) heta^i = heta^{i-1}- eta riangledown L^n( heta^{i-1}) ag{11} θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) ( 1 1 )
此时不需要像之前那样对所有的数据进行处理,只需要计算某一个例子的损失函数Ln,就可以赶紧update 梯度。
对比:
常规梯度下降法走一步要处理到所有二十个例子,但随机算法此时已经走了二十步(每处理一个例子就更新)
比如有个函数:
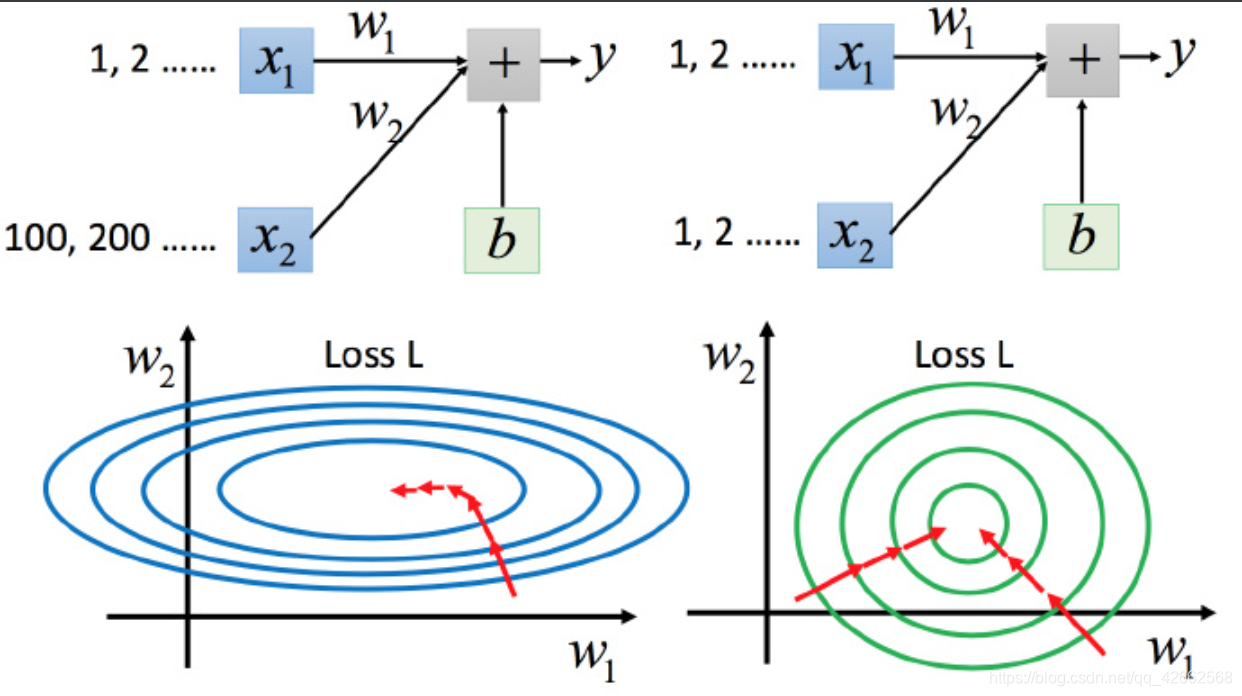
y = b + w 1 x 1 + w 2 x 2 (12) y=b+w_1x_1+w_2x_2 ag{12} y = b + w 1 x 1 + w 2 x 2 ( 1 2 )
上图左边是 x 1 x_1 x 1 x 2 x_2 x 2 w 1 w_1 w 1 w 2 w_2 w 2 w 1 w_1 w 1 y y y x 2 x_2 x 2 y y y
坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 w 1 w_1 w 1 y y y w 1 w_1 w 1 w 1 w_1 w 1 w 1 w_1 w 1 x 2 x_2 x 2 y y y x 2 x_2 x 2 x 2 x_2 x 2
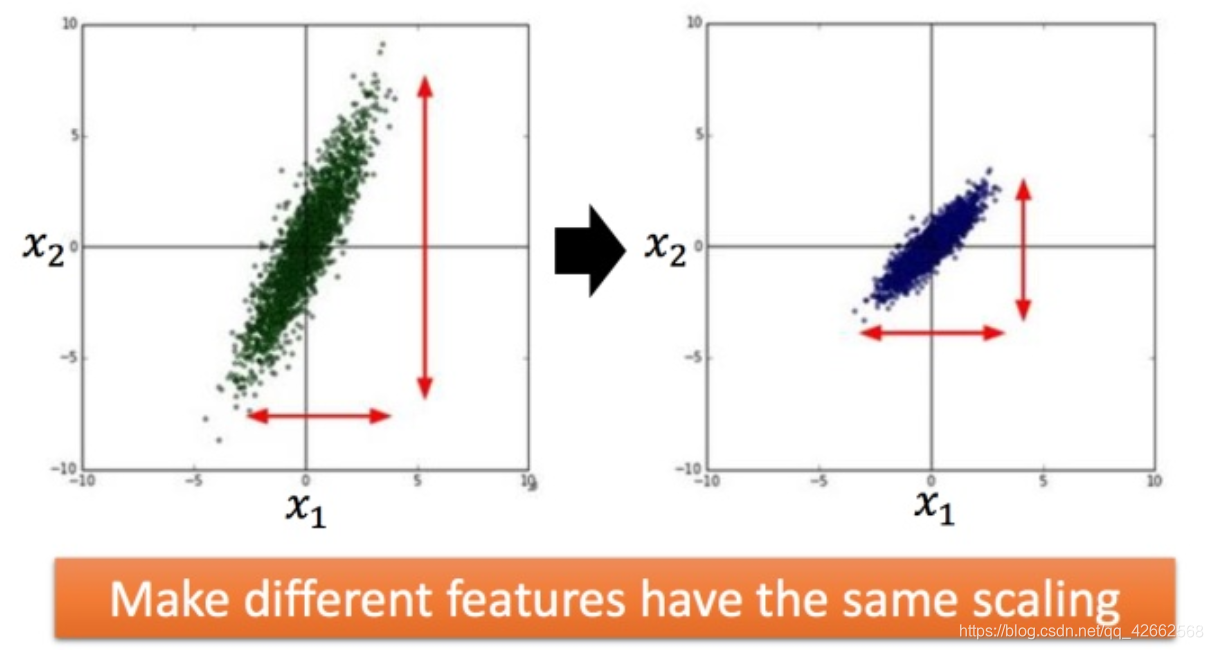
上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
方法非常多,这里举例一种常见的做法:
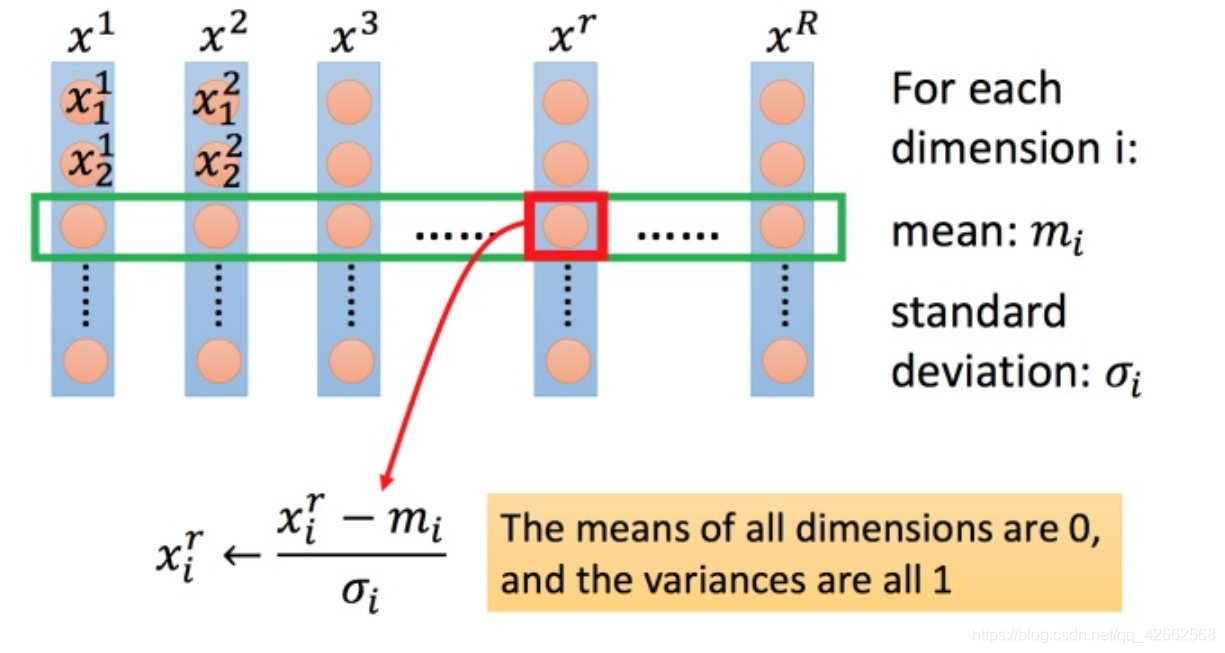
上图每一列都是一个例子,里面都有一组特征。
对每一个维度 i i i m i m_i m i σ i sigma _i σ i
然后用第 r r r i i i m i m_i m i σ i sigma _i σ i 0 0 0 1 1 1
当用梯度下降解决问题:
θ ∗ = arg max θ L ( θ ) (1) heta^∗= underset{ heta }{operatorname{arg max}} L( heta) ag1 θ ∗ = θ a r g m a x L ( θ ) ( 1 )
每次更新参数 θ heta θ θ heta θ
L ( θ 0 ) > L ( θ 1 ) > L ( θ 2 ) > ⋅ ⋅ ⋅ (13) L( heta^0) >L( heta^1)>L( heta^2)>··· ag{13} L ( θ 0 ) > L ( θ 1 ) > L ( θ 2 ) > ⋅ ⋅ ⋅ ( 1 3 )
上述结论正确吗?
结论是不正确的。。。
比如在 θ 0 heta^0 θ 0 θ 1 heta^1 θ 1
接下来就是如果在小圆圈内快速的找到最小值?
先介绍一下泰勒展开式
若 h ( x ) h(x) h ( x ) x = x 0 x=x_0 x = x 0
h ( x ) = ∑ k = 0 ∞ h k ( x 0 ) k ! ( x − x 0 ) k = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ (14)
�egin{aligned}
h(x) &= sum_{k=0}^{infty }frac{h^k(x_0)}{k!}(x-x_0)^k \
& =h(x_0)+{h}'(x_0)(x−x_0)+frac{h''(x_0)}{2!}(x−x_0)^2+⋯
ag{14}
end{aligned}
h ( x ) = k = 0 ∑ ∞ k ! h k ( x 0 ) ( x − x 0 ) k = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + 2 ! h ′ ′ ( x 0 ) ( x − x 0 ) 2 + ⋯ ( 1 4 )
当 x x x x 0 x_0 x 0 h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)≈h(x_0)+{h}'(x_0)(x−x_0) h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h ( x ) h(x) h ( x ) x = x 0 x=x_0 x = x 0 x x x
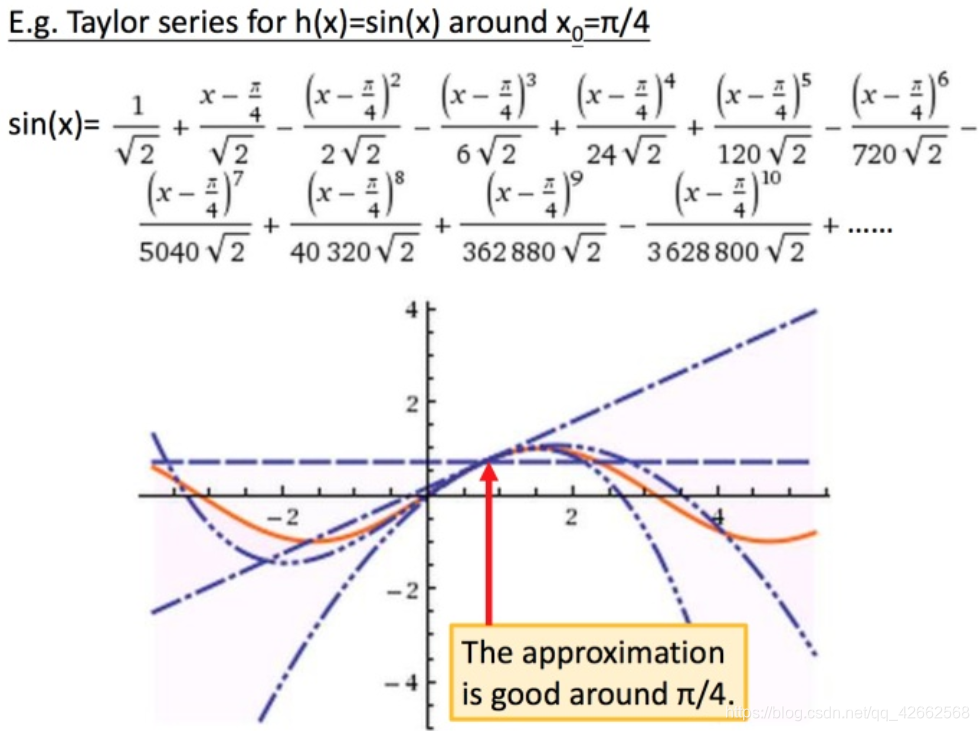
举例:
图中3条蓝色线是把前3项作图,橙色线是 s i n ( x ) sin(x) s i n ( x )
下面是两个变量的泰勒展开式
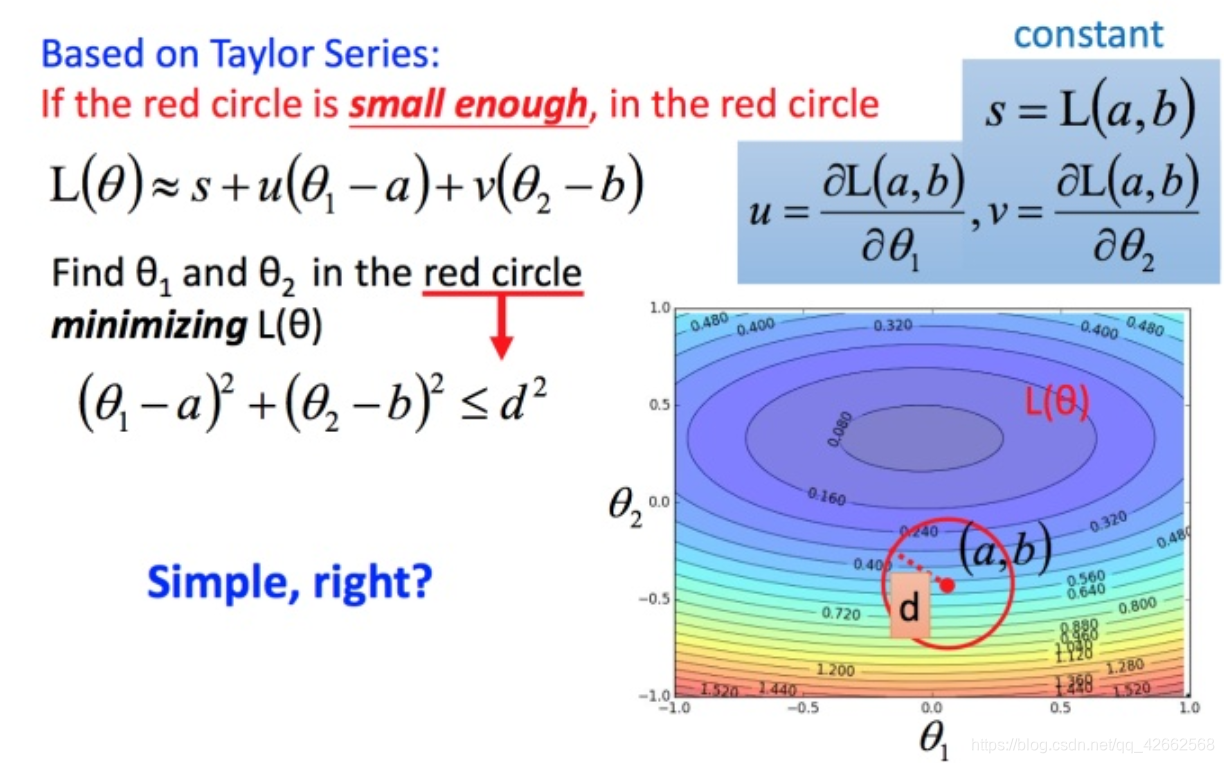
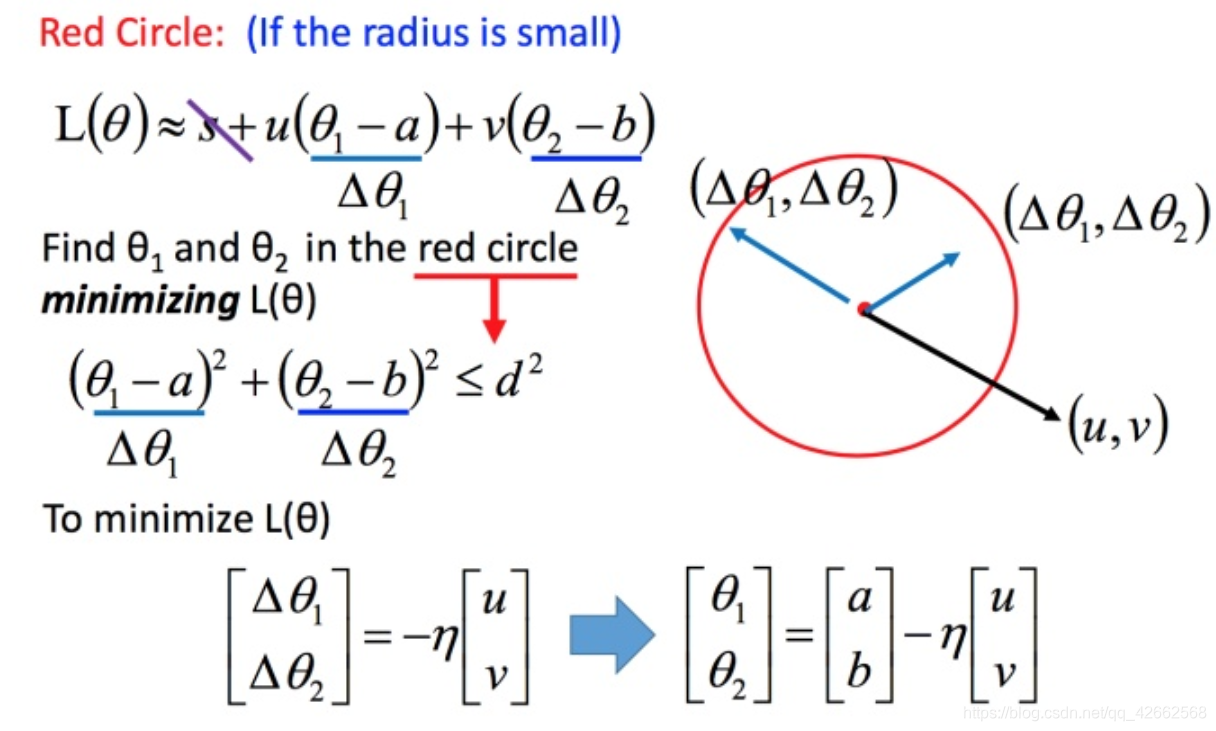
回到之前如何快速在圆圈内找到最小值。基于泰勒展开式,在 ( a , b ) (a,b) ( a , b )
将问题进而简化为下图:
( △ θ 1 , △ θ 2 ) ( riangle heta_1, riangle heta_2) ( △ θ 1 , △ θ 2 ) ( u , v ) (u,v) ( u , v ) ( u , v ) (u,v) ( u , v )
然后将u和v带入。
L ( θ ) ≈ s + u ( θ 1 − a ) + v ( θ 2 − b ) (14) L( heta)approx s+u( heta_1 - a)+v( heta_2 - b) ag{14} L ( θ ) ≈ s + u ( θ 1 − a ) + v ( θ 2 − b ) ( 1 4 )
发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圈圈足够小(也就是学习率足够小)来保证。所以理论上每次更新参数都想要损失函数减小的话,即保证式1-2 成立的话,就需要学习率足够足够小才可以。
所以实际中,当更新参数的时候,如果学习率没有设好,是有可能式1-2是不成立的,所以导致做梯度下降的时候,损失函数没有越来越小。
式1-2只考虑了泰勒展开式的一次项,如果考虑到二次项(比如牛顿法),在实际中不是特别好,会涉及到二次微分等,多很多的运算,性价比不好。
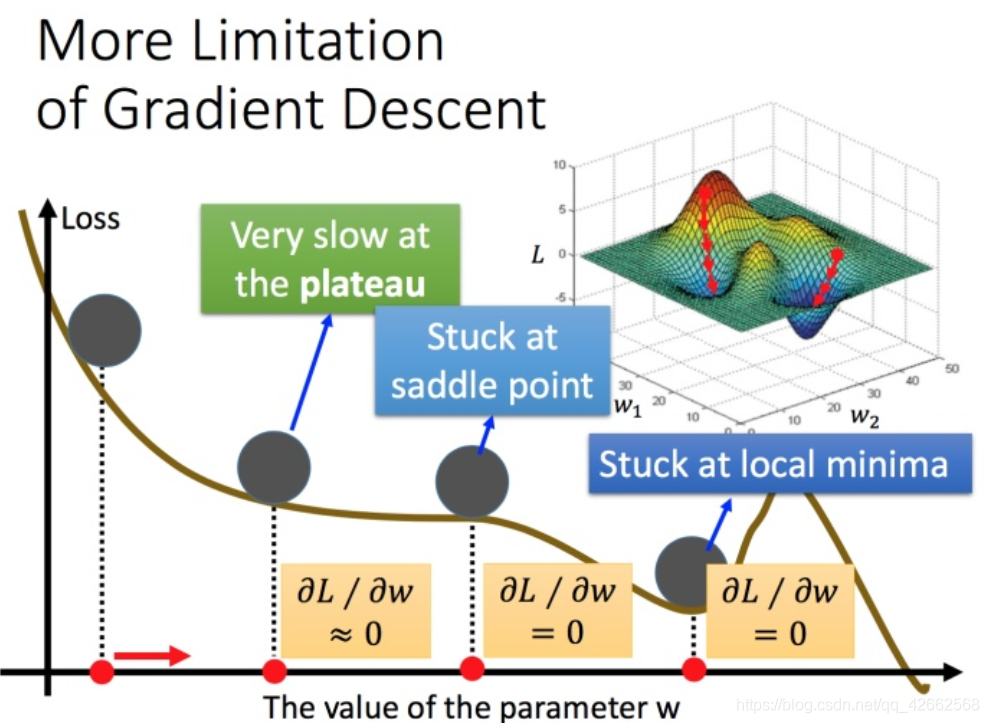
容易陷入局部极值
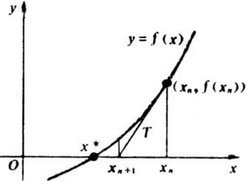
一般来说,牛顿法主要应用在两个方面,1:求方程的根;2:最优化。
牛顿法: f ( x ) f(x) f ( x ) g ( x ) = ∇ f ( x ) g(x)=
abla f(x) g ( x ) = ∇ f ( x ) H ( x ) H(x) H ( x ) ε varepsilon ε f ( x ) f(x) f ( x ) x ∗ x^{*} x ∗
取初始点 x ( 0 ) x^{(0)} x ( 0 ) k = 0 k=0 k = 0 g k = g ( x ( k ) ) g_{k}=gleft(x^{(k)}
ight) g k = g ( x ( k ) ) ∥ g k ∥ < ε left|g_{k}
ight|<varepsilon ∥ g k ∥ < ε x ∗ = x ( k ) x^{*}=x^{(k)} x ∗ = x ( k ) H k = H ( x ( k ) ) H_{k}=Hleft(x^{(k)}
ight) H k = H ( x ( k ) ) p k p_{k} p k H k p k = − g k H_{k} p_{k}=-g_{k} H k p k = − g k x ( k + 1 ) = x ( k ) + p k x^{(k+1)}=x^{(k)}+p_{k} x ( k + 1 ) = x ( k ) + p k k = k + 1 k=k+1 k = k + 1
[1] https://zhuanlan.zhihu.com/p/37524275 .https://www.leiphone.com/news/201907/DLDxLHJodhuT9h2X.html .李宏毅机器学习2019