[笔记] 浅谈线段树

（被某D姓大佬嘲讽了。。于是乎安利一发大佬的树状数组：https://www.luogu.org/blog/ddy/qian-tan-shu-zhuang-shuo-zu-post）

---

 线段树是个好东西

这篇文章主要是讲一讲

基础，自己的心得；

好，那就开始！

一.定义

线段树（Segment Tree）是一棵

二叉搜索树
树上每个节点代表一个区间[ l , r ]
同一层的节点所代表的区间，相互不会重叠

同一层节点所代表的区间，加起来是个连续的区间

对于每一个非叶结点所表示的结点 [ l , r ]，

其左儿子表示的区间为 [ l , ( l + r ) / 2 ] （[ l , ( l + r ) >>1 ]）

右儿子表示的区间为 [ ( l + r ) / 2 + 1, r ] (除法去尾取整) ( [ ( l + r ) >> 1 + 1 , r ] )

叶子节点表示的区间长度为1

ps: a * 2 = a << 1 ;

a * 2 + 1 = a << 1 | 1 ;
(下文 全部用位运算替代)

#define ll long long
struct node{
ll l,r,sum,add,mul;
}t[M<<2];

M为数列元素数 （M<<2=M*4），l是左端点，r是右端点，sum为数列区间[ l , r ]中所有元素总和，add为加法标记，mul为乘法标记（与lazy是一个意思，不懂的后面会讲）

开四倍空间证明

证明：
设共有N个节点，则有

ceil（log2（n））层，

所以共需要2^(ceil(log2(n))+1)-1节点

 个人理解：其实就是将一个数列不断二分，直到区间只有一个叶子节点。而每个节点的父节点具有在一定情况下能代表其所有子节点的性质（比如求和时，t[a].sum=t[a<<1].sum+t[a<<1|1].sum），从而通过访问父节点，得到性质，节省访问子节点的时间，降低时间复杂度

如图

二.操作

　　1.建树

　　　　void build(根节点（一般是1），左端点，右端点)

　　　　先二分区间（层层递归），直至区间左端点等于右端点，这意味着到达叶子节点，所以读取数据；

　　　　　最后递归回去，求得区间的sum值。

void build(ll tr,ll l,ll r)
{
    t[tr].l=l,t[tr].r=r,t[tr].mul=1;
    if(l==r)
    {
        t[tr].sum=g();  //inline ll g() 快读
        return ;
    }
    R ll mid=(l+r)>>1;
    build(tr<<1,l,mid);
    build(tr<<1|1,mid+1,r);
    t[tr].sum=t[tr<<1].sum+t[tr<<1|1].sum;
}

　　2.改变元素的值

　　　　（1）加法

　　　　　　void add（根节点，左端点，右端点，增量）

　　　　　　在现有区间（这是由根节点决定的->相当于通过根确定子树->从而确定区间），二分区间位置　　

　　　　　　如果递归时，现有区间就是所要更改的区间，那么直接更改整个区间的sum，使sum+=inc*（r-l+1）（就是增量*区间长度），同时add+=inc（不能是add=inc，因为add可能不为0），add表示的是[l,r]区间中所有的叶子节点都少加了add，而之所以要有这个add是为了减少不必要的操作（此时没必要把每个子节点的值都修改）（其实原因就是上文：每个节点的父节点具有在一定情况下能代表其所有子节点的性质，从而通过访问父节点，得到性质，节省访问子节点的时间，降低时间复杂度）

　　　　　　　　　　　　而所要更改的区间的左端点如果大于现有区间的mid，则递归右半区间；

　　　　　　　　　　　　而所要更改的区间的右端点如果小于现有区间的mid，则递归左半区间；

　　　　　　　　　　　　而所要更改的区间就在现有区间内的的话，分别递归区间[l,mid]和[mid+1,r];

　　　　　　　　　　　　细心的你（？）可能发现，为什么在后三种情况递归前，会有一些add(),和mul()运算？

　　　　　　　　　　　　因为我们记得 “每个节点的父节点具有在一定情况下能代表其所有子节点的性质” 对吧？ 我们也知道，父节点的sum是由子节点递归而来的吧？ 所以如果不下放add（此时这个操作是必要的），那么父节点的sum不能被更新，于是就不能代表子节点的性质了

如图：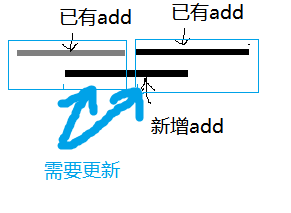

所以实际上是为了保持父节点的代表性。。

void add(ll tr,ll l,ll r,ll inc)
{
    if(t[tr].l==l&&t[tr].r==r)
    {
        t[tr].sum+=inc*(r-l+1);
        t[tr].add+=inc;
        return ;
    }
    R ll mid=(t[tr].l+t[tr].r)>>1;
    if(t[tr].mul!=1) 
        mul(tr<<1,t[tr].l,mid,t[tr].mul),mul(tr<<1|1,mid+1,t[tr].r,t[tr].mul),t[tr].mul=1;
    if(t[tr].add!=0)
        add(tr<<1,t[tr].l,mid,t[tr].add),add(tr<<1|1,mid+1,t[tr].r,t[tr].add),t[tr].add=0;
    if(l>mid) add(tr<<1|1,l,r,inc);
    else if(r<mid+1) add(tr<<1,l,r,inc);
    else add(tr<<1,l,mid,inc),add(tr<<1|1,mid+1,r,inc);
    t[tr].sum=t[tr<<1].sum+t[tr<<1|1].sum;
}

　　　　（2）乘法

　　　　　　void mul（根节点，左端点，右端点，增量）

　　　　　　你会发现，递归的过程基本相同；

　　　　　　　　那我需要解释一下，为什么先乘后加

　　　　　　　　若对[l,r]进行+1，*2，+1的操作

　　　　　　　　则实际上是（a+1）*2 + 1=2*a+2 + 1；

　　　　　　　　所以mul要sum*=inc，mul*=inc，add*=inc

　　　　　　　　所以先前的add要乘mul，再进行add

　　　　　　　　

void mul(ll tr,ll l,ll r,ll inc)
{
    if(t[tr].l==l&&t[tr].r==r)
    {
        t[tr].sum*=inc;
        t[tr].mul*=inc;
        t[tr].add*=inc;
        return ;
    }
    R ll mid=(t[tr].l+t[tr].r)>>1;
    if(t[tr].mul!=1) 
        mul(tr<<1,t[tr].l,mid,t[tr].mul),mul(tr<<1|1,mid+1,t[tr].r,t[tr].mul),t[tr].mul=1;
    if(t[tr].add!=0)
        add(tr<<1,t[tr].l,mid,t[tr].add),add(tr<<1|1,mid+1,t[tr].r,t[tr].add),t[tr].add=0;
    if(l>mid) mul(tr<<1|1,l,r,inc);
    else if(r<mid+1) mul(tr<<1,l,r,inc);
    else mul(tr<<1,l,mid,inc),mul(tr<<1|1,mid+1,r,inc);
    t[tr].sum=t[tr<<1].sum+t[tr<<1|1].sum;
}

　　　

　　　3.求和

　　　　　ll query(根节点，左端点，右端点)

　　　　你又会发现，递归的过程同add

　　　　　所以理解后就很好懂啦。

ll query(ll tr,ll l,ll r)
{
    if(t[tr].l==l&&t[tr].r==r) return t[tr].sum;
    R ll mid=(t[tr].l+t[tr].r)>>1;
    if(t[tr].mul!=1) 
        mul(tr<<1,t[tr].l,mid,t[tr].mul),mul(tr<<1|1,mid+1,t[tr].r,t[tr].mul),t[tr].mul=1;
    if(t[tr].add!=0)
        add(tr<<1,t[tr].l,mid,t[tr].add),add(tr<<1|1,mid+1,t[tr].r,t[tr].add),t[tr].add=0;
    if(l>mid) return query(tr<<1|1,l,r);
    else if(r<mid+1) return query(tr<<1,l,r);
    else return query(tr<<1,l,mid)+query(tr<<1|1,mid+1,r);
}

 三.例题

　　如洛谷P3372 P3373（说实话，我的线段树不是最快的，但还可以）（我太菜了，只做了这些）

　

其实我的思路就是

维护线段树的性质，该更新时则更新，通过访问父节点，得到性质，节省访问子节点的时间，降低时间复杂度。

如有错误，恳请您指正（我太菜了）；如有不理解，可留言，我会尽量回复。。。（高中生吐槽一波。。）

by Jackpei 2019.2.5