一,鸽巢原理的证明
1.定义:
若有$n$个鸽巢和$k*n+1$只鸽子,所有的鸽子都进入鸽巢,那么至少有一个巢中有$k+1$只鸽子(n,k≥0)。
2.证明(反证法):
若每个鸽巢中的鸽子数都不大于$k$,则总鸽子数$<=kn$,与已知矛盾。得证。(其实挺显然的吧,,,qwq)
二,小应用
1.Ramsey定理
六个人中,要么存在三个人彼此互相认识,要么存在三个人彼此都不认识;
证明:从任意一点(此处以$N_1$为例)可以引$5$条线,由鸽巢原理可知,至少有$3$条边会同色,我们钦定它为红色。
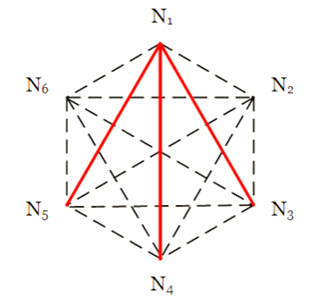
考虑此三边的终点的着色情况,将此三点中的任意两点连线着红色,即可构成一个红色的三元环
如果不用红色在$N_3,N_4,N_5$之间连边,则也会构成一个蓝色的三元环。
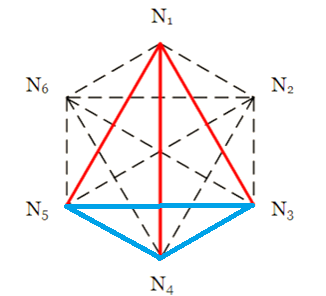
2.中国剩余定理(孙子定理)的证明:
求证:设$N,M$除了$1$以外没有公约数(即$n,m$互质),两个数字$a,b$满足$0≤a<n, 0≤b<m$,则有且只有一个$c$满足$0≤c<n*m$且$cequiv a mod space n$,$cequiv b mod space m$。
证明(反证法):设存在两个不等的数$0≤c_1,c_2<n*m$,使$c_1,c_2$关于$n,m$均同余。
那么我们不妨设$c_1<c_2$,那么设$k=c_2-c_1$,那么显然,$c_1-c_2$为$n,m$的整数倍,即$k$为$n,m$的公倍数,则有$k_{min}=lcm(n,m)$;
因为$n,m$互质,那么$k_{min}=n*m$;那么$c_2=c_1+k=c_1+n*m>=n*m$,与假设矛盾。得证。
3.一些数学定理的证明:
①求证:有理数中的无限位小数在小数点后某一位必开始循环。
证明:由有理数定义我们可设该有理数为$N/M(N,M∈Z且M!=0)$,那么根据竖式除法的原则,求值过程中不断更新的是分子$N$的值,由于不同分子都是由上次的分子对分母取模所得知,取$M$个不同的分子,那么根据鸽巢原理,他们中至少有两个数关于$M$同余,那么下一位结果也就循环了。
②求证:从$1$到$2n$中,选$n+1$个数,至少有一对数,其中一个数是另一个数的倍数;
暂时咕咕。
③求证:从$1-2n$中,选$n+1$个数,至少有一对数是互素的;
证明:我们可以将$[1,2n]$划分为n个区间$[1,2],[3,4],......,[2n-1,2n]$,那么$n+1$个数中至少有两个数来自同一区间;由相邻两数互质知$n+1$个数中,至少有一对数是互素的。
④求证:对于任意正整数 $n$ ,都能找到一个 $n$ 的倍数,它全由数字 $0$ 和 $1$ 构成,且前半部分全部为$1$,后半部分全部为$0$;(这不是某个神仙出的题吗)
证明:我们取$n$个数$1,11,111,1111,......$,$n$个$1$,由鸽巢原理知,这$n$个数中对$n$取模至少有两个数相同,设较大的数为$M$,较小的数为$m$,则易证$n|M-m$;因为$M$为长度大于$m$的1串,那么相减后$M-m$前半部分一定全部为$1$,后半部分全部为$0$.
4.小水题
2019.06.02