思路:斜率优化
提交:(2)次
错因:二分写挂
题解:
首先观察可知,
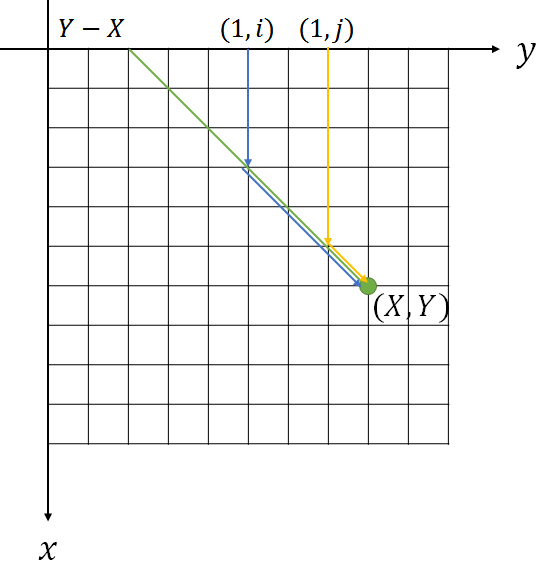
对于点(f(X,Y)),一定是由某个点((1,p)),先向下走,再向右下走。
并且有个显然的性质,若从((1,p))向下走,则(a[p]=min(a[i]),iin [p,Y])(要不然直接从后面的更小的那个位置向下走,再向右下走)
还有一个显然的性质,若(i<j)且(i)比(j)更优,则(a[i]>a[j])(上面的结论)
设(s[i]=sum_{j=1}^i a[j])
那么对于点(f(X,Y))有(ans=s[Y]-s[i]+a[i]*(X-Y+i),iin [max(1,Y-X),Y])
这个式子是可以斜率优化的:(s[i]-a[i]*i=(X-Y)*a[i]+s[Y]-ans)
要最小化(ans),就是最大化(s[Y]-ans),所以我们用单调栈维护下降斜率(上凸包),每次先查找合法区间(iin [max(1,Y-X),Y]),然后再在单调栈中二分斜率。
#include<cstdio>
#include<iostream>
#include<algorithm>
#define R register int
using namespace std;
namespace Luitaryi {
template<class I> inline I g(I& x) { x=0;
register I f=1; register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*=f;
} const int N=1e5+10;
int n,m,a[N],s[N],stk[N],ans[N],t;
struct node {int x,y,p;
inline bool operator < (const node& that) const {return y<that.y;}
}b[N];
inline int getlim(int pos) {
R l=1,r=t; while(l<r) { R md=l+r>>1;
if(stk[md]<pos) l=md+1; else r=md;
} return l;
}
inline double calc(int i,int j) {return ((double)(s[i]-a[i]*i)-(double)(s[j]-a[j]*j))/(double)(a[i]-a[j]);}
inline void main() {
g(n); for(R i=1;i<=n;++i) g(a[i]),s[i]=s[i-1]+a[i];
g(m); for(R i=1;i<=m;++i) g(b[i].x),g(b[i].y),b[i].p=i;
sort(b+1,b+m+1); for(R i=1,j=1;i<=n;++i) {
while(t&&a[stk[t]]>=a[i]) --t;
while(t>1&&calc(stk[t],i)>=calc(stk[t-1],i)) --t;
stk[++t]=i; while(b[j].y==i&&j<=m) {
R l=getlim(b[j].y-b[j].x),r=t;
while(l<r) { R md=l+r>>1;
if(calc(stk[md],stk[md+1])<b[j].x-b[j].y) r=md;
else l=md+1;
} l=stk[l],r=b[j].y;
ans[b[j].p]=s[r]-s[l]+a[l]*(b[j].x-r+l); ++j;
}
} for(R i=1;i<=m;++i) printf("%d
",ans[i]);
}
} signed main() {Luitaryi::main(); return 0;}
2019.08.12
88