剑指offer[8]——跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

做过上一道题目的同学应该对这道题目没什么问题了，这道题的实质还是一个菲波那切数列，大家有什么不明白的可以点击这里跳转。

题目中说明青蛙可以跳一级或两级台阶，我们先试着推导一下，如果是只有一级台阶，很显然只有一种跳法；如果是两级台阶的话，可以从平台跳两级台阶或者先跳到一级再跳到两级，总共有两种跳法，那么接下来到第三级台阶呢，大家有可能会发现继续按照前面的枚举方法好像不太适用。

大家应该会发现，想要跳上第三级台阶，那么在跳上第三级台阶之前就只有两个做法：

1. 从第一级台阶跳两级到第三级台阶
2. 从第二级台阶跳一级到第三级台阶

既然这样的话，是不是把跳到第一级台阶的方法数加上跳到第二级台阶的方法数就是跳上第三级台阶的方法数了呢，答案显然就是这样。

同理，跳上第四级台阶的方法数等于跳上第三级台阶的方法数加上跳上第二级台阶的方法数，推理结果如下：

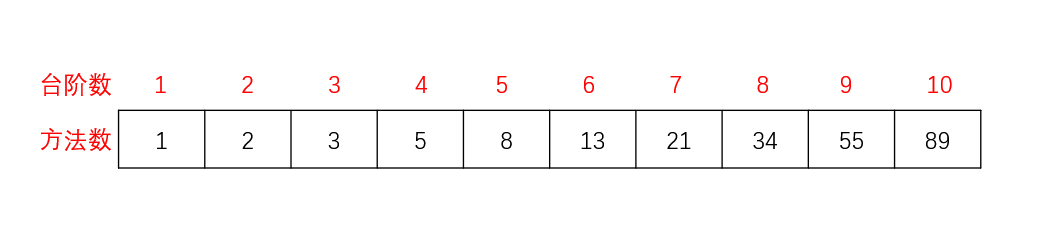
大家可以看出这就是一个斐波那契数列，算法如下：

function jumpFloor(number)
{
    let a = 1;
    let b = 2;
    while(--number!=0){
        b = a + b;
        a = b - a;
    }
    return a;
}