数据结构与算法-栈、队列、堆

一、栈、队列

预备知识：

#include  "pch.h"
#include <iostream>
#include <stdio.h>
#include <stack>
int main()
{
    std::stack<int> S;
    if (S.empty())
    {
        printf("S is empty");
    }
    S.push(5);
    S.push(6);
    S.push(10);
    printf("S.top = %d
", S.top());
    S.pop();
    S.pop();
    printf("S.top = %d
", S.top());
    printf("S.size = %d
", S.size());
    return 0;
}

//S.top() 取出栈顶
//S.empty() 判断栈是否为空
//S.push(x) 把x压入栈
//S.pop() 弹出栈顶
//S.size() 栈的存储元素个数

#include  "pch.h"
#include <iostream>
#include <stdio.h>
#include <queue>
int main()
{
    std::queue<int> Q;
    if (Q.empty()) 
    {
        printf("Q is empty!
");
    }
    Q.push(5);
    Q.push(6);
    Q.push(10);
    printf("Q.front = %d
", Q.front());
    Q.pop();
    Q.pop();
    printf("Q.front = %d
", Q.front());
    Q.push(1);
    printf("Q.back = %d
", Q.back());
    printf("Q.size = %d
", Q.size());
    return 0;
}

//Q.front() 取出队列头部元素
//Q.back() 取出队列尾部元素
//Q.empty() 判断队列是否为空
//Q.push(x) 把x添加至队列
//Q.pop() 弹出队列头部元素
//Q.size() 返回队列的存储元素个数

1.用队列实现栈

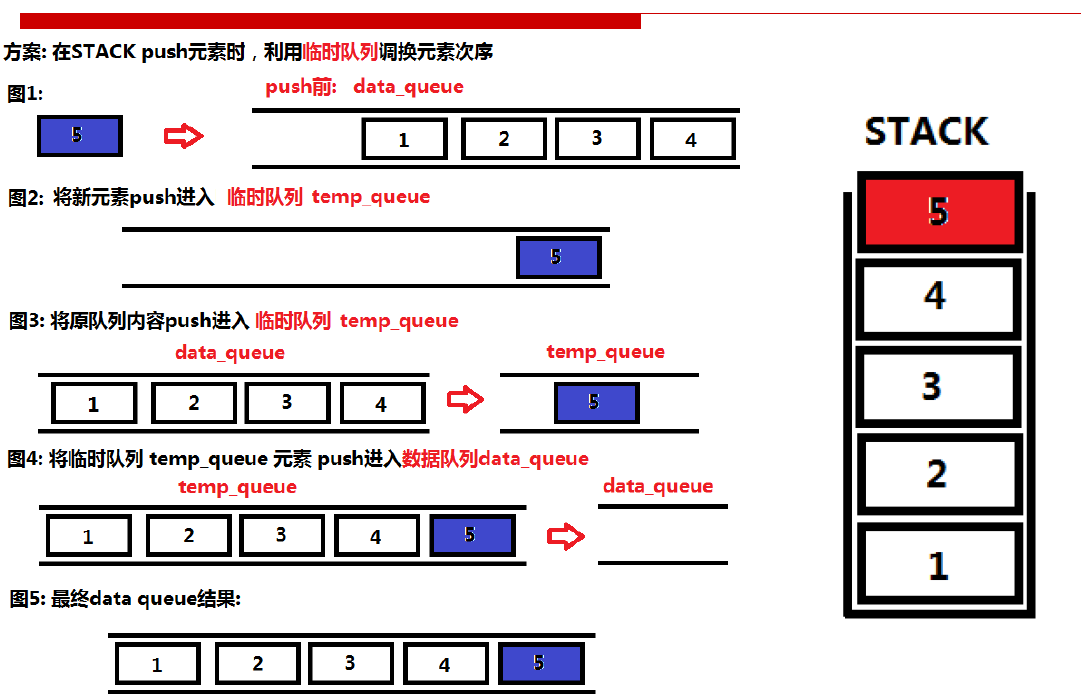
要求栈用队列实现，即在队列里面实现“后进先出”，所以把新进来的元素放入临时队列（temp_queue）中，再把原来的队列中的元素添加至临时队列中，形成了最后新进来的元素在最前面。

代码实现如下：

class MyStack {
public:
    /** Initialize your data structure here. */
    MyStack() {
        
    }
    
    /** Push element x onto stack. */
    void push(int x) {
        std::queue<int> tem_queue;
        tem_queue.push(x);
       while(!_data.empty()) 
       {
           tem_queue.push(_data.front());
           _data.pop();
       }
       while(!tem_queue.empty())
       {
           _data.push(tem_queue.front());
           tem_queue.pop();
       }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int x =_data.front();
        _data.pop();
        return x;
    }
    
    /** Get the top element. */
    int top() {
        return _data.front();
    }
    

2.用栈实现队列

 

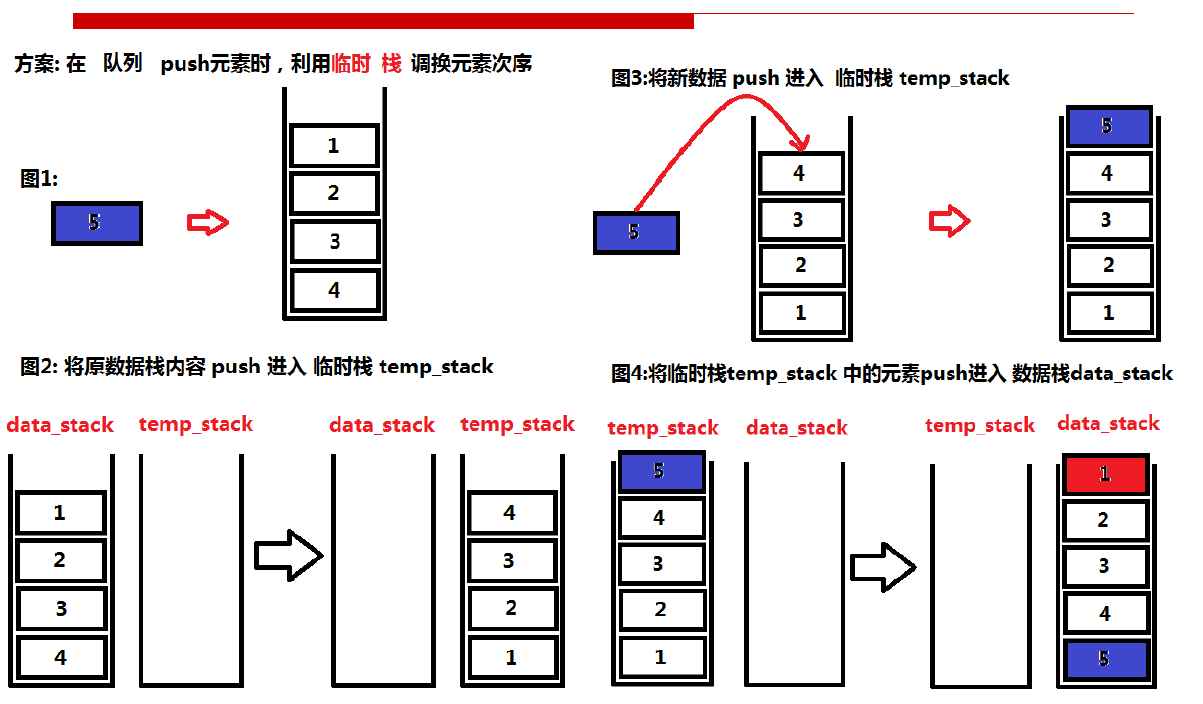
将原数据压入临时栈，再讲新数据压入临时栈，之后将临时栈数据压入原栈。

class MyQueue {
public:
    /** Initialize your data structure here. */
    MyQueue() {
        
    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        std::stack<int>tem_stack;
        while(!_data.empty())
        {
            tem_stack.push(_data.top());
            _data.pop();
        }
        tem_stack.push(x);
        while(!tem_stack.empty())
        {
            _data.push(tem_stack.top());
            tem_stack.pop();
        }
        
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        int x = _data.top();
        _data.pop();
        return x;
    }
    
    /** Get the front element. */
    int peek() {
        return _data.top();
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return _data.empty();
    }
private:
    std::stack<int>_data;
};

3.包含min函数的栈

 

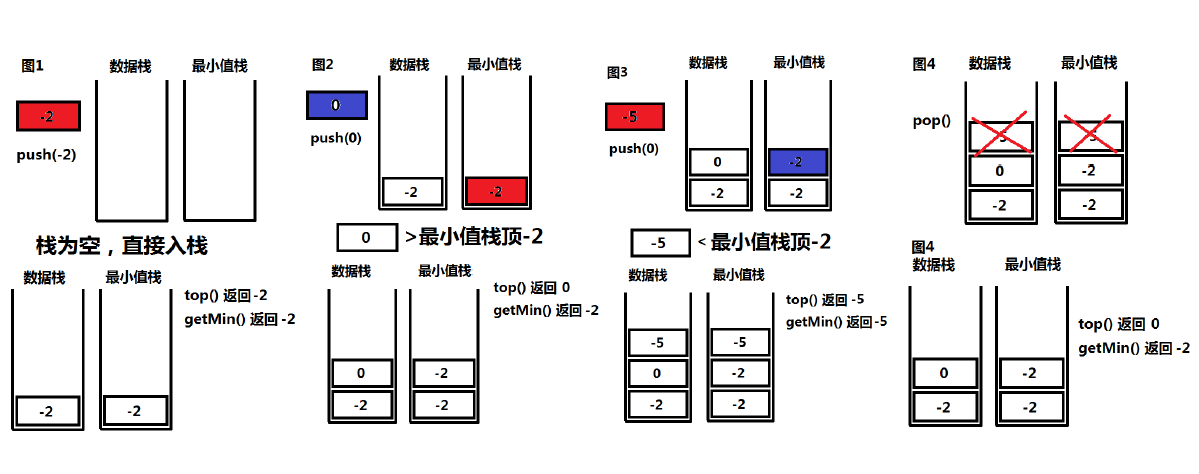
class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {  
    }
    
    void push(int x) {
        _data.push(x);
        if (_min.empty())
        {
           _min.push(x); 
        }
        else
        {
            if(x > _min.top())
                x = _min.top();
                _min.push(x);
        }
    }
    
    void pop() {
        _data.pop();
        _min.pop();
    }
    
    int top() {
        return _data.top();
    }
    
    int getMin() {
        return _min.top();
    }
private:
    std::stack<int>_data;
    std::stack<int>_min;
};

4.合法的出栈序列

5.简单的计算器

二、堆

预备知识：

#include  "pch.h"
#include <iostream>
#include <stdio.h>
#include <queue>
int main()
{
    std::priority_queue<int>big_heap;
    std::priority_queue<int, std::vector<int>, std::greater<int>>small_heap; 
    std::priority_queue<int, std::vector<int>, std::less<int>>big_heap2;
    if (big_heap.empty())
    {
        printf("big_heap is empty!
");
    }
    int test[] = { 6, 10, 1, 7, 99, 4,33 };
    for (int i = 0; i < 7; i++)
    {
        big_heap.push(test[i]);
    }
    printf("big_heap.top = %d
", big_heap.top());
    big_heap.push(1000);
    printf("big_heap.top = %d
", big_heap.top());
    for (int i = 0; i < 3; i++)
    {
        big_heap.pop();
    }
    printf("big_heap.top= %d
", big_heap.top());
    printf("big_heap.size = %d
", big_heap.size());

}

1.数组中第K大的数

 

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
        std::priority_queue<int, std::vector<int>, std::greater<int>> Q;
        for(int i = 0; i< nums.size(); i++)
        {
            if(i < k) #这里我觉得是i < k
            {
                Q.push(nums[i]);
            }
            else if(nums[i] >  Q.top())
            {
                Q.pop();
                Q.push(nums[i]);
            }
        }
        return Q.top();   
    }
};

2.寻找中位数

 第一种情况：

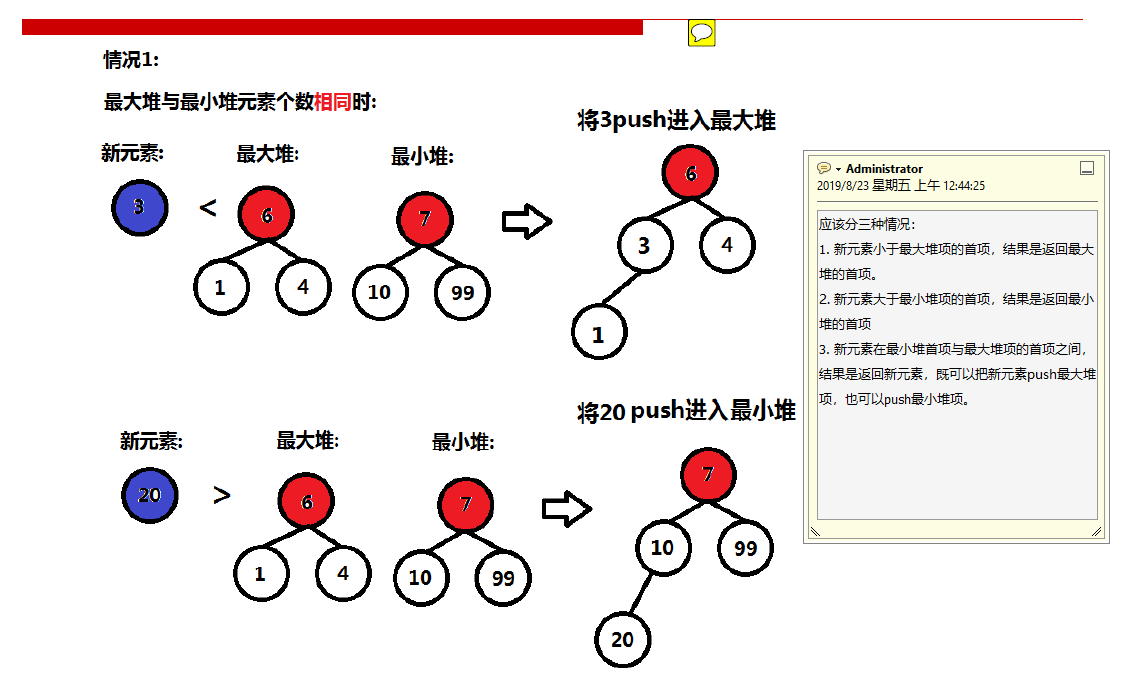
第二种情况：

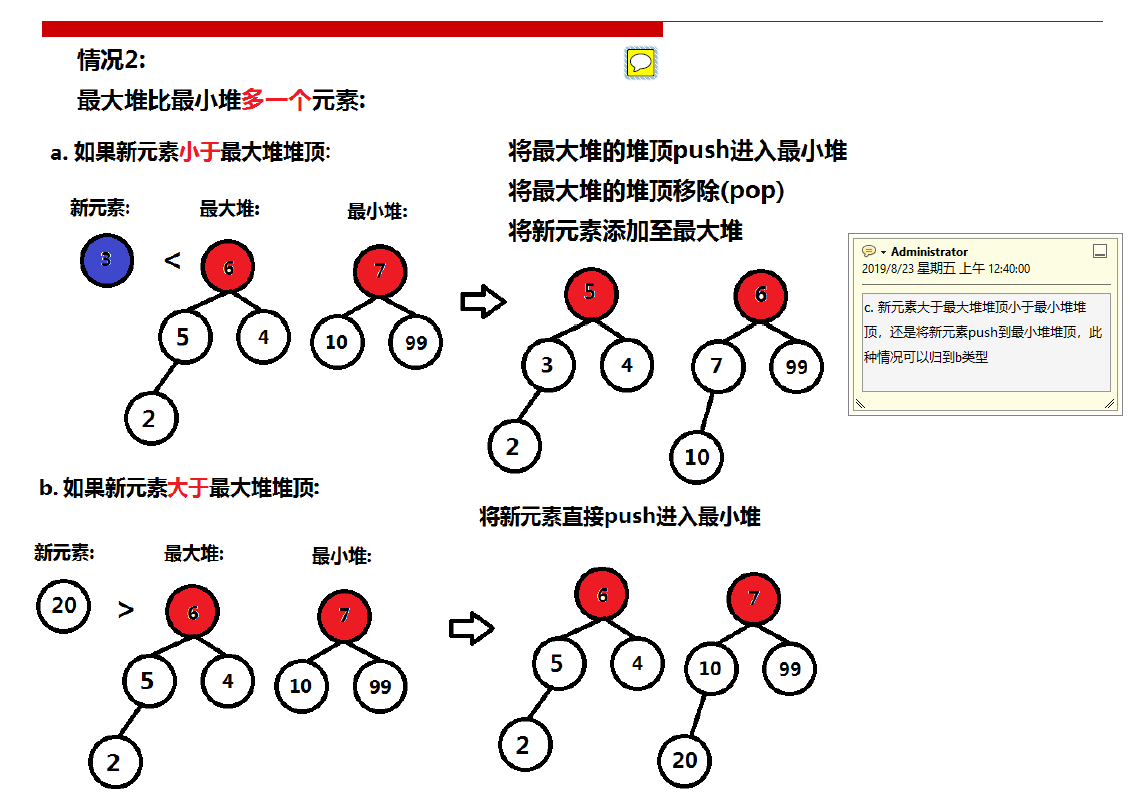
第三种情况：

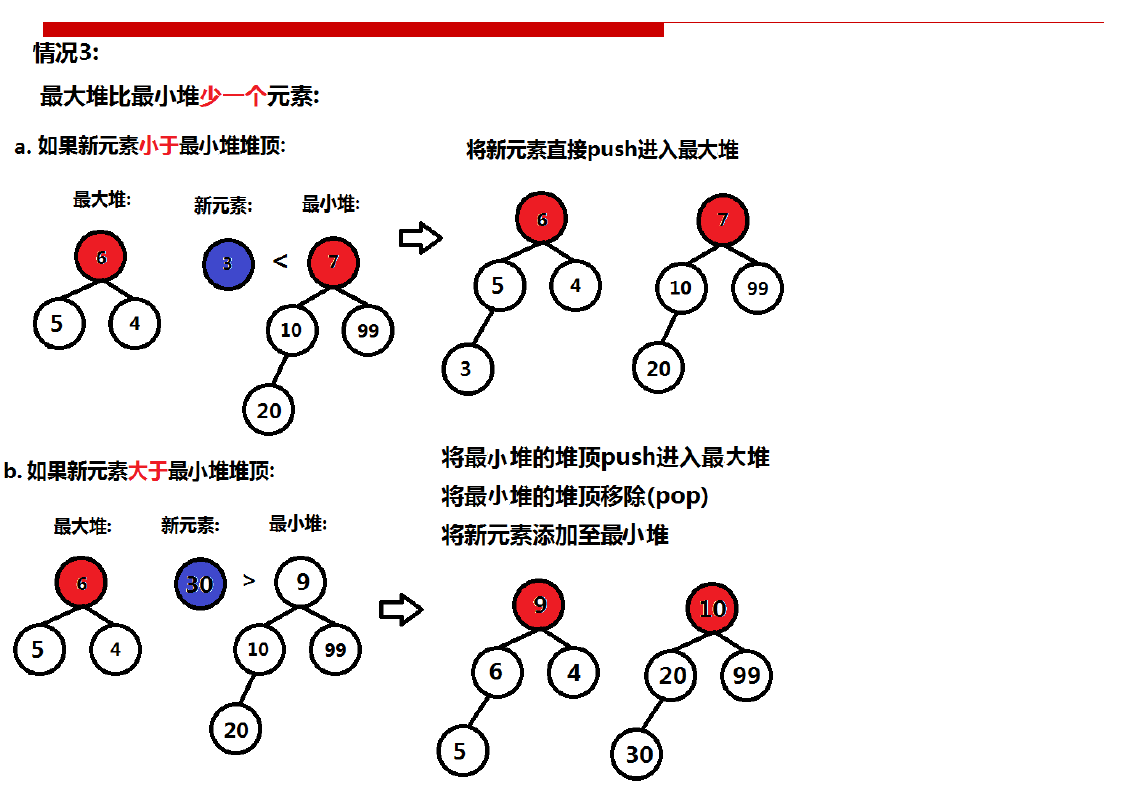
class MedianFinder {
public:
    /** initialize your data structure here. */
    std::priority_queue<int, std::vector<int>, std::greater<int>>small_queue;
    std::priority_queue<int, std::vector<int>, std::less<int>>big_queue;
    MedianFinder() {
    }
    void addNum(int num) {
        if (big_queue.empty())
        {
            big_queue.push(num);
            return;
        }
        if (big_queue.size() == small_queue.size())
        {
            if (num < big_queue.top())
            {
                big_queue.push(num);
            }
            else{
                small_queue.push(num);
            }
        }
        else if (big_queue.size() > small_queue.size() )
        {
            if(num > big_queue.top()){
                small_queue.push(num);
            }
            else{
                small_queue.push(big_queue.top());
                big_queue.pop();
                big_queue.push(num);
            }
        }
        else if(small_queue.size() > big_queue.size() )
        {
            if(num < small_queue.top()){
                big_queue.push(num);
            }
            else{
                big_queue.push(small_queue.top());
                small_queue.pop();
                small_queue.push(num);
            }
        }
    }
    
    double findMedian() {
        if(big_queue.size() == small_queue.size()){
            return (float((big_queue.top()) + small_queue.top()) / 2);  //注意需要进行浮点数转换
        }
        else if(big_queue.size() > small_queue.size()){
            return big_queue.top();
        }
        return small_queue.top();
    }
};