单源最短路径算法---Dijkstra

Dijkstra算法树解决有向图G=（V，E）上带权的单源最短路径问题，但是要求所有边的权值非负。

解题思路：

　　V表示有向图的所有顶点集合，S表示那么一些顶点结合，从源点s到该集合中的顶点的最终最短路径的权值(程序中用dist[i]表示)已经确定。算法反复选择具有最短路径估计的顶点u 属于 V-S（即未确定最短路径的点，程序中finish[i]=false的点），并将u加入到S中(用finish[i]=true表示)，最后对u的所有输出边进行松弛。

程序实现：

     输入数据：

　　　　

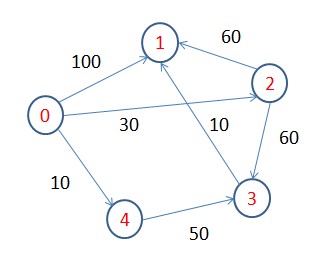
5 7

0 1 100

0 2 30

0 4 10

2 1 60

2 3 60

3 1 10

4 3 50

/*************************************************************************
    > File Name: Dijkstra.cpp
    > Author: He Xingjie
    > Mail: gxmshxj@163.com
    > Created Time: 2014年06月07日 星期六 22时12分43秒
    > Description: 
 ************************************************************************/
#include<iostream>
#include<cstdio>

using namespace std;

#define INF 99999

//map矩阵记录路径图，dist[i]表示源点到节点
//i的最短路径,finish[i]表示节点i找到最短路径
//path[i]=j表示从源节点到i节点的最短路径要经过j
int map[100][100], dist[100], finish[100];
int path[100];

void Dijkstra(int s, int n)
{
/*
 *s为源点，n为节点的个数
 *当finish[i]=true时，dist[i]
 *为s到i的最短路径
 *假设S为已求得最短路径的终点集合
 *V为所有节点的集合
 */
    int i, j, v, k;
    
    //初始化dist[i]
    for (i=1; i<n; i++)
    {
        dist[i] = map[s][i];
        if (dist[i] < INF)
            path[i] = s;
    }

    //初始化源节点
    finish[s] = true;
    dist[s] = 0;

    for (i=1; i<n; i++)  //总共有n-1个节点
    {
        int min = INF;
        for (j=0; j<n; j++)      
        {
            //从V-S中(没有找到最短路径的集合)寻找离源节点
            //距离最近的点
            if (!finish[j] && dist[j] < min)
            {
                v = j;
                min = dist[j];
            }
        }
        //找到最短路径
        finish[v] = true;    //把节点v加入到S中
    
        //松弛(Relax)
        for (k=0; k<n; k++)
        {
            if (!finish[k] && map[v][k] != INF)
                if (dist[k] > dist[v] + map[v][k])
                {
                    dist[k] = dist[v] + map[v][k];
                    path[k] = v;
                }
        }
    }
}

void PrintPath(int k)
{
    if (k == 0)
    {
        printf("%d", k);
        return;
    }

    PrintPath(path[k]);
    printf("->%d", k);
}

void PrintMap(int n)
{
    int i, j;
    //输出矩阵
    for (i=0; i<n; i++)
    {
        for (j=0; j<n; j++)
        {
            if (map[i][j] == INF)
                printf("INF ");
            else
                printf("%d  ", map[i][j]);
        }

        printf("
");
    }
}

int main()
{
    int n, m, i, j;

    freopen("input.txt", "r", stdin);
    cin>>n>>m;    //n是顶点数，m是边数

    //初始化
    for (i=0; i<n; i++)
    {
        finish[i] = false;
        for (j=0; j<n; j++)
            map[i][j] = INF;
    }

    //输入
    for(int i=1; i<=m; i++)
    {
        int i,j;
        cin>>i>>j;
        cin>>map[i][j];
    }

    /*
     *PrintMap(n);
     */

    Dijkstra(0, n);

    for (i=1; i<n; i++)
    {
        printf("Path: ");
        PrintPath(i);
        printf("  Dist:%d
", dist[i]);
    }

    return 0;
}

参考：

http://www.cnblogs.com/dolphin0520/archive/2011/08/26/2155202.html   

http://blog.csdn.net/hnuzengchao/article/details/7534690