#include<iostream> #include<algorithm> #include<string> #include<cstring> using namespace std; long long C(int m, int n) { int k = 1;// 相当于 C(m,n) long long ans=1; while(k<=n) { ans=((m-k+1)*ans)/k; k++; } return ans; } int main() { printf("%lld", C(10 ,5)); }
方法二:杨辉三角打表
原理:C(n,m)=C(n-1,m-1)+C(n-1,m)
#include<iostream> using namespace std; int n,m; long long c[10005]; int main() { cin>>n>>m; m=min(m,n-m);//因为C[n][m]=C[n][n-m],所以m可以取m和n-m中小的那一个,以节省时间。 c[0]=1; for (int i=1;i<=n;i++) { for (int j=m;j>=1;j--) { c[j]=c[j]+c[j-1]; } } cout<<c[m]; }
求解思路:
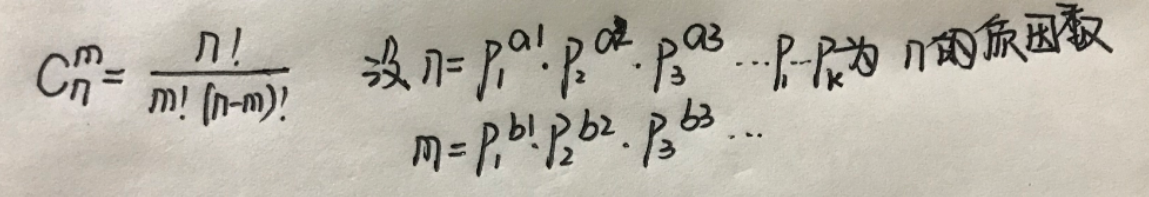
1. 筛法求出范围内的所有质数。
2. 通过 C(n, m) = n! / m! / (n - m)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
3. 用高精度乘法将所有质因子相乘。
代码
#include<iostream> #include<algorithm> #include<vector> using namespace std; int prime[1000],cnt=0,rat[1000]; bool p[1000]; void findprime(int n)//欧拉筛来找素数 { for (int i = 2; i <= n; i++) { if (!p[i]) prime[cnt++] = i; for (int j = 0; j < cnt; j++) { if (i*prime[j] > n)break; p[i*prime[j]] = true; if (i%prime[j] == 0)break; } } } int rate(int n, int p)//分解质因数,求得每个质因数在n!中的出现个数 { int res = 0; while (n) { res += n / p; n /= p; } return res; } vector<int>mul(vector<int>a, int b)//高精度乘法*低精度数字(此时的a一直是反着的,所以最后反着输出) { vector<int>answer; int t=0;//进位数 for (int i = 0; i < a.size(); i++) { t += a[i] * b; answer.push_back(t % 10); t /= 10; } while (t)//处理最高位的数字,防止最高位的数字大于9 { answer.push_back(t % 10); t /= 10; } return answer; } int main() { int n, m; scanf("%d %d", &n, &m); findprime(n); for (int i = 0; i < cnt; i++) rat[i] = rate(n, prime[i]) - rate(m, prime[i]) - rate(n - m, prime[i]);//计算每个质因数的幂的次数 vector<int>fin; fin.push_back(1); for (int i = 0; i < cnt; i++)//所有质因数的迭代 for (int j = 0; j < rat[i]; j++)// rat[i]是每个质因数在合数中的次数,所以这里是将每个质因数乘rat[i]次 fin = mul(fin, prime[i]); for (int i = fin.size() - 1; i >= 0; i--) printf("%d", fin[i]); }
1.欧拉筛来找素数
如果对欧拉筛不熟悉,点击此处查看。
2.分解质因数,求得每个质因数在n!中的出现个数
求N!中素因子p的个数,也就是N!中p的幂次
公式为:cnt=[n/p]+[n/p^2]+[n/p^3]+...+[n/p^k];
例如:N=12,p=2
12/2=6,表示1~12中有6个数是2的倍数,即2,4,6,8,10,12
12/2^2=6/2=3,表示1~12中有3个数是4的倍数,即4,8,12,它们能在提供2的基础上多提供一个2
12/2^3=3/2=1,表示1~12中有1个数是8的倍数,即12,它能在提供两个2的基础上又多提供一个2
代码就是
int rate(int n, int p)//分解质因数,求得每个质因数在n!的出现个数 { int res = 0; while (n) { res += n / p; n /= p; } return res; }
效果:
例如求c(5,3),则通过代码首先要计算5的质因数:2 3 5;
之后分别计算每个质因数在n中的出现个数:rate(2)=3;rate(3)=1;rate(5)=1;而5!=5 * 4 * 3 * 2 *1;其中将合数转换为素数,则2出现的个数就是rate(2)的值:3次(一个4,一个2,相当于3个2),3、5的出现次数各为1
而每个质因数在n!的出现的个数就是每个质因数在n!中对应的幂数
3.使用C(n, m) = n! / m! / (n - m)! 这个公式求出每个质因子的次数
我们上一步计算出了每个质因数在n!中的幂数,而类比就能求出在m!、(n-m)!中的幂数,而C(n, m) = n! / m! / (n - m)! 这个式子的值就是各个质因子在n!中的幂数-在m!中的幂数-在(n-m)!中的幂数,即
for (int i = 0; i < cnt; i++) rat[i] = rate(n, prime[i]) - rate(m, prime[i]) - rate(n - m, prime[i]);//计算每个质因数的幂的次数
4.高精度乘法计算结果
至此,我们将C(n, m)的值转换为了多个质因子的若干幂次方的乘积,我们通过高精度*低精度来计算(大数运算知识:请点击此处了解)
vector<int>mul(vector<int>a, int b)//高精度乘法*低精度数字(此时的a一直是反着的,所以最后反着输出) { vector<int>answer; int t=0;//进位数 for (int i = 0; i < a.size(); i++) { t += a[i] * b; answer.push_back(t % 10); t /= 10; } while (t)//处理最高位的数字,防止最高位的数字大于9 { answer.push_back(t % 10); t /= 10; } return answer; }
在大数的乘法计算中,首先是要把原来的大数求逆后再从前往后计算,最后再将答案逆序输出,但是此时看似vector<int>
其实这里的原因是vector<int>a的初始化其实是1,这里的1要理解成已经是求逆后的(单个数字求逆还是原数)
例如:初始a中是1,令b=5;开始1 *5 =5;vector<int>p中是5
再调用mul函数,就是5 *5 =25;此时vector<int>p中是52
再调用mul函数,就是25 *5 =125;此时vector<int>p中是521
最后逆序输出就是125
for (int i = 0; i < cnt; i++)//所有质因数的迭代 for (int j = 0; j < rat[i]; j++)// rat[i]是每个质因数在合数中的次数,所以这里是将每个质因数乘rat[i]次 fin = mul(fin, prime[i]);
最后将所有的质因子都乘rat[i]遍,再去乘别的质因子,最后将结果逆序输出就是C(n, m)的值
https://blog.csdn.net/weixin_33895016/article/details/94615900