C++-POJ3233-Matrix Power Series[矩阵乘法][快速幂]

构造矩阵

 

 

 

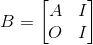
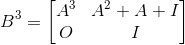
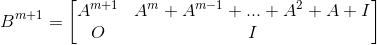
#include <cstdio>
const int MAXN=100;
struct Matrix{int a[MAXN][MAXN];}O,I;int N;
void OI(int n){N=n;for(int i=0;i<MAXN;i++)for(int j=0;j<MAXN;j++)O.a[i][j]=0,I.a[i][j]=(i==j);}
Matrix Mul(Matrix A,Matrix B,int MOD){
    Matrix C=O;
        for(int i=1;i<=N;i++)
            for(int j=1;j<=N;j++)
                for(int k=1;k<=N;k++)
                    C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%MOD;
    return C;
}
Matrix Pow(Matrix A,int n,int MOD){
    Matrix B=I;
    for(;n;A=Mul(A,A,MOD),n>>=1)if(n&1)B=Mul(B,A,MOD);
    return B;
}
Matrix B(int n){
    Matrix B=O;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&B.a[i][j]);
    for(int i=1;i<=n;i++)
        B.a[i+n][i+n]=B.a[i][i+n]=1;
    return B;
}
int main(){
    int n,m,k;scanf("%d%d%d",&n,&m,&k),OI(2*n);
    Matrix A=Pow(B(n),m+1,k);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)
            printf("%d ",(A.a[i][j+n]-(i==j)+k)%k);
        puts("");
    }
    return 0;
}