错排问题:
编号为 1 , 2 ,……, n 的 n 个元素排成一列,若每个元素所处位置的序号都与它的编号不同,则称这个排列为n个不同元素的一个错排。记 n 个不同元素的错排总数为 D(n)
D0=? n=0 <=>不存在元素=>不存在元素满足条件=>D0=1
D1=0,D2=1,D3=2
对于D3的所有方案为2,见下
2 3 1
3 1 2
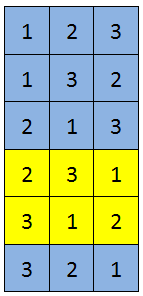
第一类:元素4任意放在前3位(i)中,元素i放在第四位(相当于swap),其余2个任意错排(D2)D4=???
第二类:前3个已经错排(D3)任意交换前3位和第四位
4 3 2 1 3 1 2 4=>4 1 2 3 2 3 1 4=>4 3 1 2
3 4 1 2 3 1 2 4=>3 4 2 1 2 3 1 4=>2 4 1 3
2 1 4 3 3 1 2 4=>3 1 4 2 2 3 1 4=>2 3 4 1
整理得:
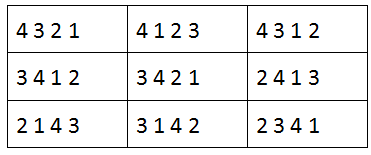
同理:Dn=(n-1)(Dn-1+Dn-2)D4=3*(D2+D3)=3*(1+2)=9
下面求通项公式
1.容斥法:
设Ai为数i还在原位的总方案数
|Ai|=(n-1)! (i=1~n)
|Ai∩Aj|=(n-2)! (i,j=1~n,i!=j)
…
| A1∩A2∩A3∩…∩An|=1
每个元素都不在原位的总方案数:
Dn=|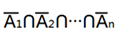 |
|
=n!-C(n,1)(n-1)!+C(n,2)(n-2)!+…±C(n,n)1!
=n!(1-1/1!+1/2!-1/3!+…±1/n!)
2.构造法
令En=Dn/n!= Dn-1*(n-1)/n! + Dn-2 *(n-1)/n!
=(1-1/n)(En-1-En-2)
令Fn=En-En-1
=(-1/n)(En-1-En-2)
Fn=(-1/n)Fn-1
=(-1/n)(-1/n-1)Fn-2
…
=E1-E0=-1
回带
En=(-1)^n/n!+(-1)^(n-1)/(n-1)!+…+(-1)^2/2!
Dn=n!En
=n!(1-1/1!+1/2!-1/3!+…±1/n!)
Dn≈n!e^-1
解答完毕