0x01 均匀分布
1) 离散随机变量的均匀分布:假设 X 有 k 个取值:x1, x2, ..., xk 则均匀分布的概率密度函数为:
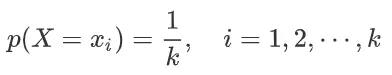
2) 连续随机变量的均匀分布:假设 X 在 [a, b] 上均匀分布,则其概率密度函数为:
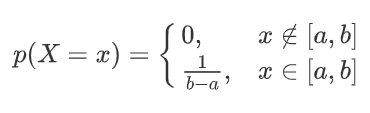
0x02伯努利分布
伯努利分布:参数为 θ∈[0,1],设随机变量 X ∈ {0,1},则概率分布函数为
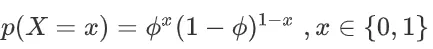
期望:
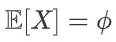
方差:
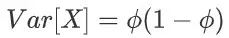
0x03 二项分布
假设试验只有两种结果:成功的概率为 θ,失败的概率为 1-θ. 则二项分布描述了:独立重复地进行 n 次试验中,成功 x 次的概率。
概率密度函数:
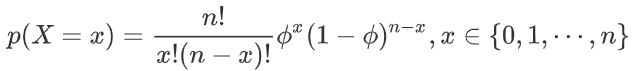
期望:
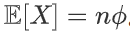
方差:
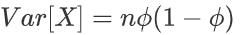
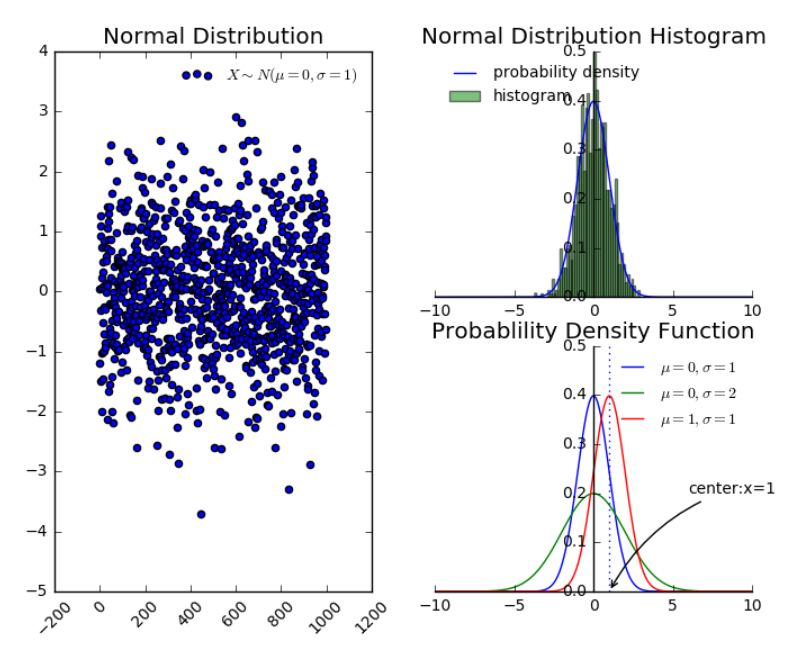
0x04 高斯分布
正态分布是很多应用中的合理选择。如果某个随机变量取值范围是实数,且对它的概率分布一无所知,通常会假设它服从正态分布。有两个原因支持这一选择:
''' 建模的任务的真实分布通常都确实接近正态分布。中心极限定理表明,多个独立随机变量的和近似正态分布。 在具有相同方差的所有可能的概率分布中,正态分布的熵最大(即不确定性最大)。 '''
典型的一维正态分布的概率密度函数为 :
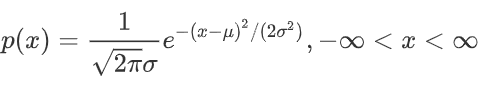
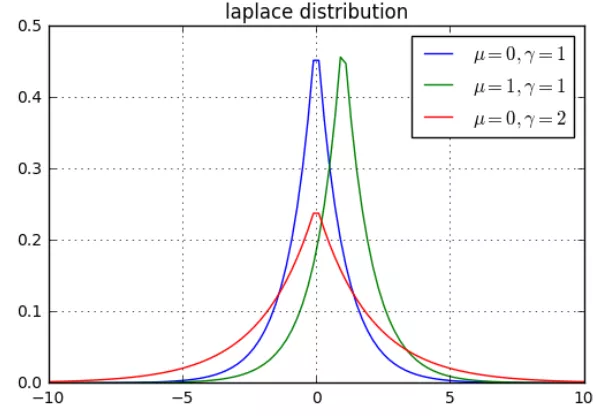
0x05 拉普拉斯分布
概率密度函数:
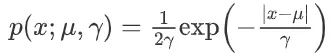
期望:
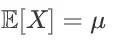
方差:
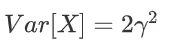
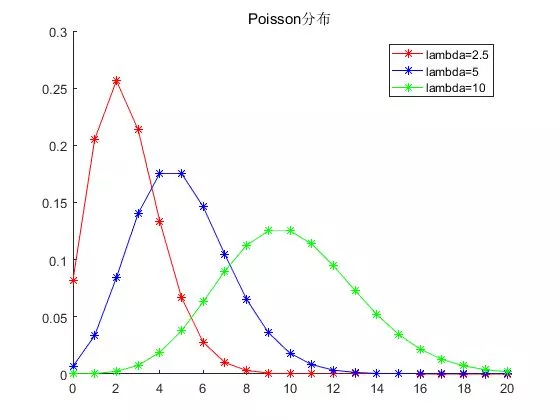
0x06 泊松分布
假设已知事件在单位时间(或者单位面积)内发生的平均次数为 λ,则泊松分布描述了:事件在单位时间(或者单位面积)内发生的具体次数为 k 的概率。
概率密度函数:
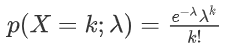
期望:
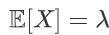
方差:
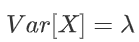
0x07 指数分布
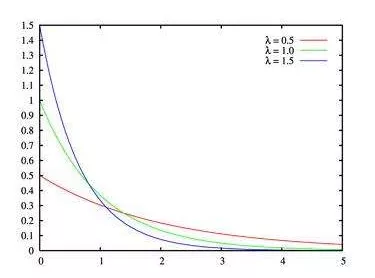
若事件服从泊松分布,则该事件前后两次发生的时间间隔服从指数分布。由于时间间隔是个浮点数,因此指数分布是连续分布。
概率密度函数:( t 为时间间隔)
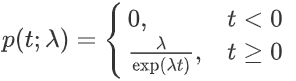
期望:
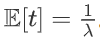
方差:
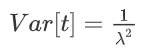
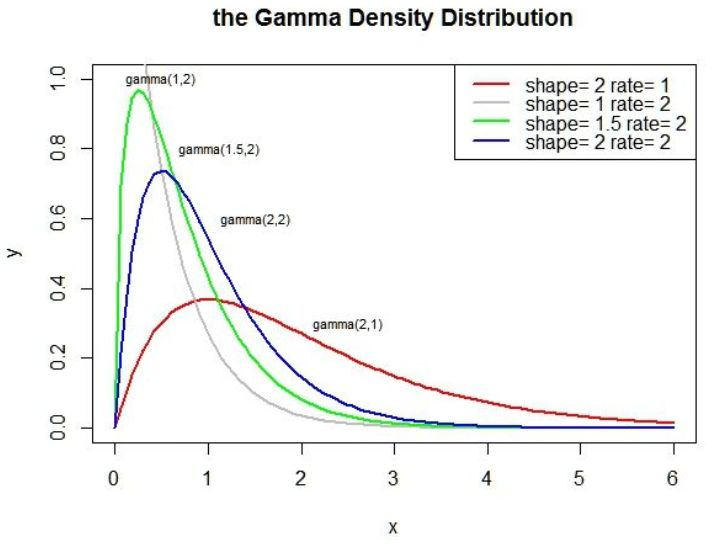
0x08 伽马分布
若事件服从泊松分布,则事件第 i 次发生和第 i+k 次发生的时间间隔为伽玛分布。由于时间间隔是个浮点数,因此伽马分布是连续分布。
概率密度函数:
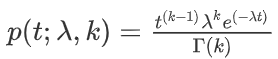
其中, t 为时间间隔,k 称为形状参数, λ 称为 尺度参数
期望和方差分别为:

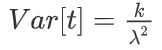
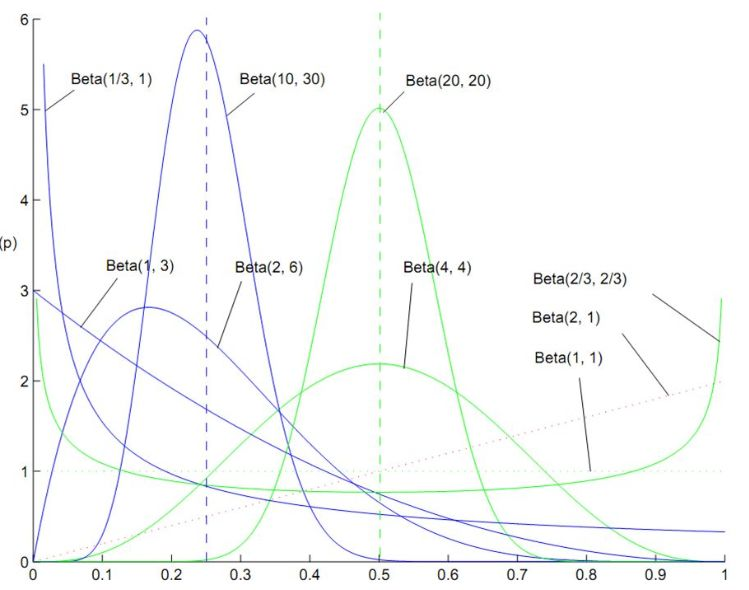
0x09 贝塔分布
贝塔分布是定义在 (0,1) 之间的连续概率分布。
如果随机变量 X 服从贝塔分布,则其概率密度函数为:
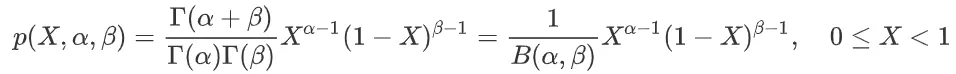
记做
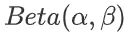
期望为:
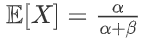
方差为:
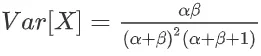
0x0A 狄拉克分布
狄拉克分布:假设所有的概率都集中在一点 μ上,则对应的概率密度函数为:
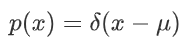
其中 δ(.)为狄拉克函数,其性质为:

狄拉克分布的一个典型用途就是定义连续型随机变量的经验分布函数。假设数据集中有样本
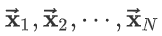
则定义经验分布函数:
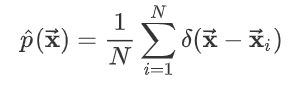
它就是对每个样本赋予了一个概率质量
对于离散型随机变量的经验分布,则经验分布函数就是多项式分布,它简单地等于训练集中的经验频率。
经验分布的两个作用:
''' 通过查看训练集样本的经验分布,从而指定该训练集的样本采样的分布(保证采样之后的分布不失真)。 经验分布就是使得训练数据的可能性最大化的概率密度函数。 '''
0x0B 多项式分布与狄里克雷分布
多项式分布的质量密度函数:
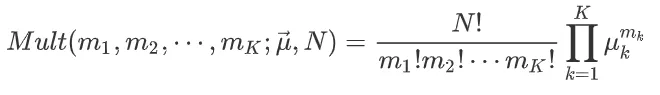
狄利克雷分布的概率密度函数:
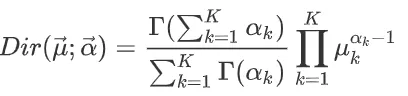
可以看到,多项式分布与狄里克雷分布的概率密度函数非常相似,区别仅仅在于前面的归一化项:
''' 多项式分布是针对离散型随机变量,通过求和获取概率。 狄里克雷分布时针对连续型随机变量,通过求积分来获取概率。 '''