前言:
分治法是将问题划分成一些独立的子问题,递归地求解各子问题,然后合并子问题的解而得到原问题的解。
动态规划(Dynamic Programming)是通过组合子问题的解而解决整个问题。它适用于子问题不是独立的情况,也就是各个子问题包含公共的子问题。在这种情况下,若用分治法会做许多不必要的工作,即重复地求解公共的子问题。动态规划对每个子问题只求解一次,将其结果保存在一张表中,从而避免每次遇到各个子问题时重新计算答案。
动态规划通常用于最优化问题。【此类问题可能有很多种可行解,我们希望找到一个具有最优值的解】。
动态规划算法设计步骤:
1、描述最优解的结构。
2、递归定义最优解的值。
3、按自底向上的方式计算最优解的值。
4、由计算出的结果构造一个最优解。
经典动态规划例题之一:装配线调度问题。
问题描述:
Colonel汽车公司在有两条装配线上的工厂内生产汽车,如下图所示。每条装配线上有n个装配站,编号为j=1,2,......,n。将装配线i(i为1或2)的第j个装配站表示为Si,j 。装配线1的第j个站和装配站2的第j个站执行相同的功能,但是由于装配站性能不同,所需要的装配时间各不相同。把在装配站Si,j上所需的时间表示为ai,j,汽车底盘进入装配线i的时间为ei,离开装配线i的时间为xi。
正常情况下,汽车在一条装配线上完成装配。当有紧急订单时,允许汽车从任一装配站上移动至另外一条装配线上,以加快装配速度,但是仍然要经过n道工序。从Si,j移动至另外一条装配线的时间表示为ti,j,i=1,2,j=1,2,3,...,n-1(第n个之后,装配已经完成)。
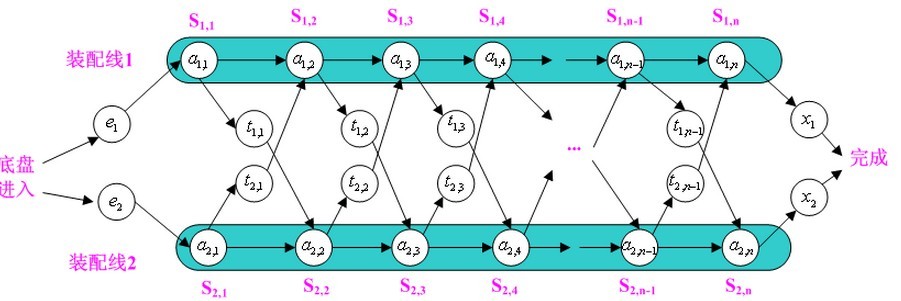
目标是确定选择装配线1和2中的哪些站,以使汽车制造时间最短?
实例解题:
对于下图实例,

结果序列:S1,1,S2,2,S1,3,S2,4,S2,5,S1,6
时间结果:2+(7)+2+(5)+1+(3)+1+(4)+(5)+1+(4)+3 = 38
解题步骤:
1、描述最优解结构的特征
动态规划方法的第一个步骤是描述最优解结构的特征。对于装配线问题,可以考虑从起始点到装配站S1,j的最快路线:如果j=1,则只有一条路线,对于j=2,3,..., n,则有两种选择:
从装配站S1,j-1直接通过S1,j;
从装配站S2,j-1,转移至S1,j后通过,移动代价为t2,j-1;
分别考虑这两种可能,它们之间具有很多共性。
首先,假设通过装配站S1,j 的最快路线通过了S1,j-1。则它一定是利用最快路线从开始到达S1,j-1的。为什么呢?如果存在一条更快的路线通过S1,j-1,就可以采用这条路线,从而 得到通过S1,j 的更快路线,这与假设矛盾。
同样,假设通过S1,j的最快路线通过了S2,j-1。则它一定是利用最快路线从开始到达S2,j-1的。理由与上述相同。
更一般的讲,对于装配线调度问题,一个问题的最优解(找出通过Si,j的最快路线)包含了子问题(找出通过S1,j-1或者S2,j-1的最快路线)的一个最优解。这种性质叫最优子结构, 这是判断是否可以用动态规划方法的标志之一。
利用子问题的最优解来构造原问题的最优解。对于装配线调度问题,推理如下:观察一条通过S1,j的最快路线,会发现它必定是经过装配线1或2的装配站j-1.因此,通过装配站S1,j的最快路线只能是以下二者之一:
通过S1,j-1的最快路线,然后直接通过装配站S1,j;
通过S2,j-1的最快路线,从2线移到1线,然后通过S1,j;
同样道理,通过S2,j的最快路线也只能是以下二者之一:
通过S2,j-1的最快路线,然后直接通过装配站S2,j;
通过S1,j-1的最快路线,从1线移到2线,然后通过S2,j;
那么,为了寻找通过任一条装配线上装配站j的最快路线,要解决它的子问题:确定两条装配线上通过装配站j-1的最快路线。
2、递归求解
第二个步骤是利用子问题的最优解来递归定义一个最优解的值。对于装配线调度问题,选择在两条装配线上通过装配站j的最快路线作为子问题,j=1,2,....., n。令fi[j]表示一个从起点 到装配站Si,j的最快时间。最终目标是确定汽车通过工厂的所有路线中的最快路线和时间,最快时间表示为f*。最终必须经过装配站n,到达工厂出口。那么有:
f* = min{f1[n]+x1,f2[n]+x2}
而,推理f1[1]和f2[1]也比较容易:
f1[1]=e1+a1,1
f2[1]=e2+a2,1
现在考虑如何计算fi[j],其中j=2,3,......,n(i=1,2)。对于f1[j],通过S1,j的最快路线或者是通过S1,j-1后直接通过S1,j,或者是通过装配站S2,j-1,从线2移动至线1后,通过S1,j。
第一种情况下,f1[j]=f1[j-1]+a1,j,第二种情况下,f1[j]=f2[j-1]+t2,j-1+a1,j,因此:
f1[j]=min{f1[j-1]+a1,j,f2[j-1]+t2,j-1+a1,j} 其中j=2,3,... n。对称的有:
f2[j]=min{f2[j-1]+a2,j,f1[j-1]+t1,j-1+a2,j} 其中j=2,3, ... n。
对于实例中的fi[j]和f*,如下表所示:
| j | 1 | 2 | 3 | 4 | 5 | 6 |
| f1[j] | 9 | 18 | 20 | 24 | 32 | 35 |
| f2[j] | 12 | 16 | 22 | 25 | 30 | 37 |
| f* | 38 |
表中的fi[j]就是子问题的最优解的值。为了有助于跟踪最优解的过程,定义li[j]为装配线的编号(或为1或为2),其上的装配站j-1被通过装配站Si,j的最快路线所用,这里 i=1,2且 j=2,3, ... n,(li[1]没有意义,因为装配站1前面没有装配站)。此外,定义l*表示装配线编号,其上的装配站n被最快路线使用。实例中的li[j]和l*如下表所示:
| j | 2 | 3 | 4 | 5 | 6 |
| l1[j] | 1 | 2 | 1 | 1 | 2 |
| l2[j] | 1 | 2 | 1 | 2 | 2 |
| l* | 1 |
通过上表可以找到一个最快路线,从l*=1开始,使用装配站S1,6,l1[6]=2则使用装配站S2,5,l2[5]=2则使用S2,4,l2[4]=1则使用S1,3,l1[3]=2则使用S2,2,l2=1则使用S1,1。
3、计算时间
写一个递归算法来计算最快路线的时间不难,但是,这种递归算法的执行时间是关于n的指数形式。如果在递归的方式中以不同的顺序来计算fi[j]的值,就能节省时间。对于j>1,fi[j]的值仅仅依赖于f1[j-1]和f2[j-1]的值。通过以递增装配站编号j的顺序来计算fi[j]的值,就可以在O(n)时间内的得到最快路线及花费的时间。下面给出FASTEST-WAY算法进行计算程序,其输入为:ai,j ,ti,j ,ei 和xi 以及n。
1 //装配线调度问题动态规划算法实现 2 public void Fastest_Way(int [][]a,int [][] t,int [] e,int [] x,int n) 3 { 4 5 f[0][0] = e[0]+a[0][0]; 6 f[1][0] = e[1]+a[1][0]; 7 for(int j=1;j<=n-1;j++) 8 { 9 10 if(f[0][j-1]+a[0][j]<=f[1][j-1]+t[1][j-1]+a[0][j]) 11 { 12 f[0][j] = f[0][j-1]+a[0][j]; 13 l[0][j] = 1; 14 } 15 else 16 { 17 f[0][j] = f[1][j-1]+t[1][j-1]+a[0][j]; 18 l[0][j] = 2; 19 } 20 if(f[1][j-1]+a[1][j]<=f[0][j-1]+t[0][j-1]+a[1][j]) 21 { 22 f[1][j] = f[1][j-1]+a[1][j]; 23 l[1][j] = 2; 24 } 25 else 26 { 27 f[1][j] = f[0][j-1]+t[0][j-1]+a[1][j]; 28 l[1][j] = 1; 29 } 30 } 31 if(f[0][n-1]+x[0]<=f[1][n-1]+x[1]) 32 { 33 fend = f[0][n-1]+x[0]; 34 lend = 1; 35 } 36 else 37 { 38 fend = f[1][n-1]+x[1]; 39 lend = 2; 40 } 41 }
4、构造路线
计算出时间后,需要构造最快路线经过的装配站,第二部分已经说明了做法。下面程序以站号递减的顺序输出最快路线的结果序列。
1 //打印结果序列(站点号递减顺序) 3 public void PrintFastWay() 4 { 5 int i = lend; 6 System.out.println("line "+i+",Station"+n); 7 for(int j=n;j>=2;j--) 8 { 9 i = l[i-1][j-1]; 10 System.out.println("line "+i+",Station"+ (j-1)); 11 } 12 }
程序实现:
1 package dynamic; 2 3 public class FastWay { 4 5 private int [][] a ; 6 private int [][] t ; 7 private int [] e; 8 private int [] x; 9 private int n; 10 11 private int fend; 12 private int lend; 13 private int [][] f; 14 private int [][] l; 15 16 public void setA(int [][] a) { 17 this.a = a; 18 } 19 public int [][] getA() { 20 return a; 21 } 22 23 public int[][] getT() { 24 return t; 25 } 26 27 public void setT(int[][] t) { 28 this.t = t; 29 } 30 31 public int[] getE() { 32 return e; 33 } 34 35 public void setE(int[] e) { 36 this.e = e; 37 } 38 39 public int[] getX() { 40 return x; 41 } 42 43 public void setX(int[] x) { 44 this.x = x; 45 } 46 47 public int getN() { 48 return n; 49 } 50 51 public void setN(int n) { 52 this.n = n; 53 } 54 55 56 57 58 public int getFend() { 59 return fend; 60 } 61 public void setFend(int fend) { 62 this.fend = fend; 63 } 64 65 public int getLend() { 66 return lend; 67 } 68 public void setLend(int lend) { 69 this.lend = lend; 70 } 71 public int[][] getF() { 72 return f; 73 } 74 public void setF(int[][] f) { 75 this.f = f; 76 } 77 public int[][] getL() { 78 return l; 79 } 80 public void setL(int[][] l) { 81 this.l = l; 82 } 83 84 //装配线调度问题动态规划算法实现 85 public void Fastest_Way(int [][]a,int [][] t,int [] e,int [] x,int n) 86 { 87 88 f[0][0] = e[0]+a[0][0]; 89 f[1][0] = e[1]+a[1][0]; 90 for(int j=1;j<=n-1;j++) 91 { 92 93 if(f[0][j-1]+a[0][j]<=f[1][j-1]+t[1][j-1]+a[0][j]) 94 { 95 f[0][j] = f[0][j-1]+a[0][j]; 96 l[0][j] = 1; 97 } 98 else 99 { 100 f[0][j] = f[1][j-1]+t[1][j-1]+a[0][j]; 101 l[0][j] = 2; 102 } 103 if(f[1][j-1]+a[1][j]<=f[0][j-1]+t[0][j-1]+a[1][j]) 104 { 105 f[1][j] = f[1][j-1]+a[1][j]; 106 l[1][j] = 2; 107 } 108 else 109 { 110 f[1][j] = f[0][j-1]+t[0][j-1]+a[1][j]; 111 l[1][j] = 1; 112 } 113 } 114 if(f[0][n-1]+x[0]<=f[1][n-1]+x[1]) 115 { 116 fend = f[0][n-1]+x[0]; 117 lend = 1; 118 } 119 else 120 { 121 fend = f[1][n-1]+x[1]; 122 lend = 2; 123 } 124 } 125 //打印结果序列(站点号递减顺序) 126 public void PrintFastWay() 127 { 128 int i = lend; 129 System.out.println("line "+i+",Station"+n); 130 for(int j=n;j>=2;j--) 131 { 132 i = l[i-1][j-1]; 133 System.out.println("line "+i+",Station"+ (j-1)); 134 } 135 } 136 }
1 package dynamic; 2 3 public class DynamicMain { 4 5 /** 6 * @param args 7 */ 8 public static void main(String[] args) { 9 // TODO Auto-generated method stub 10 11 int [][] a = {{7,9,3,4,8,4},{8,5,6,4,5,7}}; 12 int [][] t = {{2,3,1,3,4},{2,1,2,2,1}}; 13 int [] e = {2,4}; 14 int [] x = {3,2}; 15 int n = a[1].length; 16 17 int [][] f = {{0,0,0,0,0,0},{0,0,0,0,0,0}}; 18 int [][] l = {{0,0,0,0,0,0},{0,0,0,0,0,0}}; 19 20 FastWay fastWay = new FastWay(); 21 fastWay.setA(a); 22 fastWay.setE(e); 23 fastWay.setT(t); 24 fastWay.setX(x); 25 fastWay.setN(n); 26 27 fastWay.setF(f); 28 fastWay.setL(l); 29 fastWay.setFend(0); 30 fastWay.setLend(1); 31 32 fastWay.Fastest_Way(a, t, e, x, n); 33 System.out.println("最快路线花费的时间:"); 34 System.out.println(fastWay.getFend()); 35 System.out.println("最快的路线:"); 36 fastWay.PrintFastWay(); 37 } 38 39 }
程序结果:
最快路线花费的时间:
38
最快的路线:
line 1,Station6
line 2,Station5
line 2,Station4
line 1,Station3
line 2,Station2
line 1,Station1