1.定义
图由有限个顶点和它们之间的边组成
2.图的存储结构
2.1邻接矩阵
1)邻接矩阵用两个数组表示图,一个一维矩阵存储顶点,一个二维数组(称为邻接矩阵)存储边,其元素值为边的权值,如果不存在这条边则计为无穷大(可以是INT_MAX),自己到自己的边值为0
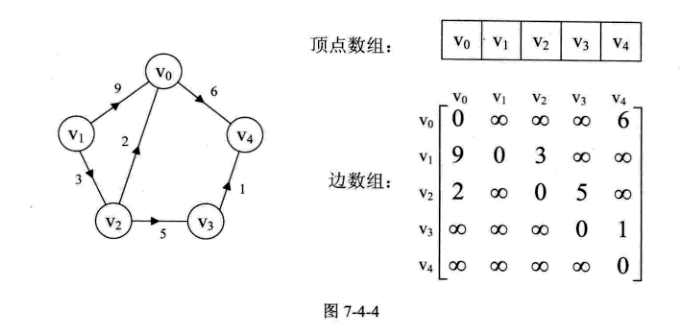
2)邻接矩阵对于边数相对顶点数较少的图,会浪费很多很多空间,如下图,这时就需要使用邻接表
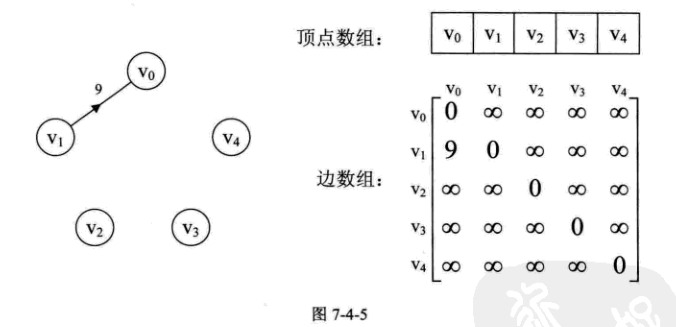
2.2邻接表
1)邻接表用一个一维数组配合链表来表示图,数组中的元素是链表,每个链表的头节点代表顶点,非头节点们代表“和头节点相邻的顶点”,非头节点还可以有一个数据部分表示“头节点到自己的这条边的权值”
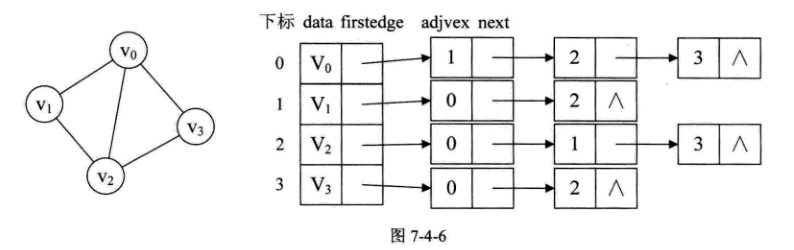

2)邻接表采用链式结构,所以遍历起来更慢
3.度
1)无向图顶点的边数叫作度,无向图边数是各顶点度数和的一半
2)有向图的顶点的度分为入度和出度
4.弧
1)图的边叫作弧
2)有向图边的起点叫作弧尾,终点叫作弧头
5.连通图
1)无向图中任意两个顶点之间都有路径相连,则该图称为连通图
6.最小生成树
1)生成树:n个顶点和n-1条边构成的连通图
2)最小生成树:权值和最小的生成树
7.prim算法求最小生成树
1)集合V是所有顶点的集合,集合U是一个顶点集合
2)最开始任选一个顶点放入集合U中
3)贪心策略:每次选取连接集合U和集合V-U的所有边中的最短边,并将这条边关联的顶点放入集合U中,直到U=V,所有这些选出来的边构成最小生成树
4)时间复杂度O(n2)
8.求无向图的所有连通图
1)深度优先搜索DFS
9.AOV网
1)AOV网(Activity On Vertex Network ):
- 一个有向图
- 顶点表示活动
- 某个活动的开始要以前一个活动结束作为先决条件
- AOV网一定不存在环路
3)拓扑序列:拓扑序列就是满足从顶点Vi到顶点Vj的一条路径,拓扑序列可能不止一个
4)拓扑排序:
- 选择一个入度为0的顶点,将它加入到拓扑序列中,删除此顶点和以此顶点为起点的边,重复上述操作,直到输出全部的顶点
- 如果顶点输出少了,则说明这个图不是AOV网
10.AOE网
1)AOE网(Activity On Vertex Edge):
- 一个有向图
- 顶点表示事件
- 有向边表示活动,边上的权值表示活动持续的时间
- 没有入度的顶点称为源点,没有出度的顶点称为终点,AOE网只有一个源点一个终点
2)AOV网和AOE网都是用来对工程建模的,AOV网描述活动之间的制约关系,AOE网是在活动制约关系之上来分析整个工程至少需要多少时间
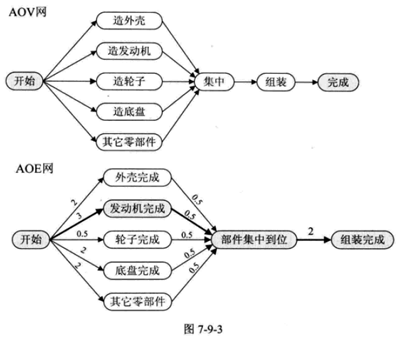
3)关键路径:
- 从源点到终点具有最长的路径叫作关键路径
- 为什么这条路径最关键?因为完成整个工程的时间只取决于这条最长的路径,不取决于其他的短路径,想要减少工程时间,就要考虑缩短关键路径
- 关键路径上的活动叫作关键活动
4)关键路径的算法:
- 找出所有的关键活动就得到关键路径了
- 事件Vi的最早发生时间:从源点到顶点Vi的最大路径长度,称为事件Vi的最早开始时间
- 事件Vi的最晚发生时间:在保证整个工程完成的前提下,事件的最晚的开始时间
- 对AOE网进行拓扑排序,如果得到的拓扑序列顶点个数小于网中顶点数,则说明网中有环存在,不能求关键路径,终止算法
- 从源点V0开始,求出各个顶点的最早发生时间Ve(i),起点的最早发生时间等于0,其余顶点的最早发生时间=所有前驱节点的最早发生时间+对应边权值,取最大值
- 从终点Vn向源点V0逆推,求所有顶点的最晚发生时间Vl(i),起点和终点的最晚发生时间等于其最早发生时间,其余顶点的最晚发生时间=所有后继节点的最晚发生时间-对应的边权值,取最小值
- 最早发生时间=最晚发生时间的事件就是关键事件
- 关键路径可能不止一条,不过它们的路径长度肯定相等