【话前叨叨】
一些日常刷题策略(转载):
PS:本题的题目信息来自洛谷平台
下面就是进入正题了(其实这也是我第一次在csdn写博客,所以写的不好的地方也请大家多多谅解和提点/微笑/)
一、score 成绩
(本文题目信息皆来自洛谷)
【题目描述】
牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:
总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%
牛牛想知道,这门课程自己最终能得到多少分。
【输入输出格式】
输入格式:
输入文件只有1行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。相邻两个数之间用一个空格隔开,三项成绩满分都是100分。
输出格式:
输出文件只有1行,包含一个整数,即牛牛这门课程的总成绩,满分也是100分。
【输入输出样例】
输入样例#1:
100 100 80
输出样例#1:
90
输入样例#2:
60 90 80
输出样例#2:
79
【说明】
输入输出样例1说明
牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
输入输出样例2说明
牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
数据说明
对于30%的数据,A=B=0。
对于另外30%的数据,A=B=100。
对于100%的数据,0≤A、B、C≤100且A、B、C都是10的整数倍。(这是关键!题目里有说都是10的倍数,所以不用什么卡精度的啦,不过后来貌似也重判了,总之卡进度的童鞋们还是要吸取教训的哈)
【分析】一句话,连暴力都不用,直接加一加,再除个十完事儿!
附上代码
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,a,b,c;
int read() //输入优化,不必在意,在这里的话也用不着
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') //判断不是数字的,过滤
c=getchar();
if(c=='-') //判断负数
{
f=-1;
c=getchar();
}
while(isdigit(c)) //判断是数字的,累加
{
x=(x<<3)+(x<<1)+c-'0'; //位运算不懂的同学可以看看蓝色的那本书
c=getchar();
}
return x*f;
}
int main()
{
cin>>a;cin>>b;cin>>c;
n=a*2+b*3+c*5; //按照题意先全都加起来然后再除10 (话说这和提前招的分数标准好像)
n/=10;
cout<<n<<endl; //输出n就好了,也可以暴力一点直接输出
//(a*2+b*3+c*5 )/10
return 0;
}那下面就进入第二题了!
二、librarian 图书管理员
【题目描述】
图书馆中每本书都有一个图书编码,可以用于快速检索图书,这个图书编码是一个 正整数。 每位借书的读者手中有一个需求码,这个需求码也是一个正整数。如果一本书的图 书编码恰好以读者的需求码结尾,那么这本书就是这位读者所需要的。 小 D 刚刚当上图书馆的管理员,她知道图书馆里所有书的图书编码,她请你帮她写 一个程序,对于每一位读者,求出他所需要的书中图书编码最小的那本书,如果没有他 需要的书,请输出-1。
【输入输出格式】
输入格式:
输入文件的第一行,包含两个正整数 n 和 q,以一个空格分开,分别代表图书馆里 书的数量和读者的数量。
接下来的 n 行,每行包含一个正整数,代表图书馆里某本书的图书编码。
接下来的 q 行,每行包含两个正整数,以一个空格分开,第一个正整数代表图书馆 里读者的需求码的长度,第二个正整数代表读者的需求码。
输出格式:
输出文件有 q 行,每行包含一个整数,如果存在第 i 个读者所需要的书,则在第 i 行输出第 i 个读者所需要的书中图书编码最小的那本书的图书编码,否则输出-1。
【输入输出样例】
输入样例#1:
5 5
2123
1123
23
24
24
2 23
3 123
3 124
2 12
2 12
输出样例#1:
23
1123
-1
-1
-1
【说明】
【数据规模与约定】
对于 20%的数据,1 ≤ n ≤ 2。
另有 20%的数据,q = 1。
另有 20%的数据,所有读者的需求码的长度均为 1。
另有 20%的数据,所有的图书编码按从小到大的顺序给出。
对于 100%的数据,1 ≤ n ≤ 1,000,1 ≤ q ≤ 1,000,所有的图书编码和需求码均 不超过 10,000,000。
【分析】
这题目其实也不难(后两题才更难),用朴素的方法就是按题目给的信息来对书号进行遍历搜索(查找长度是给了我们的,要利用起来的话大概也就是我的方法吧),代码如下:
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,a[1005],q,len,x;
int read() //如t1,这里就不解释了
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-')
{
f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
return x*f;
}
int main()
{
/* 输入部分(不包括查找部分) */
n=read();
q=read();
for(int i=0;i<n;++i)
a[i]=read();
/* 读入查找数据并查找、输出 */
for(int i=0;i<q;++i)
{
int flag=0,minn=0x3f3f3f3f; //初始一下min,0x表示16进制
len=read();
len=pow(10,len); //这里就是等下遍历到的书号取余后会剩余的位数
x=read();
for(int j=0;j<n;++j)
{
if(a[j]%len==x) //判断是否符合条件
{
flag=1;
if(a[j]<minn) //先看当前满足条件的书号是否
minn=a[j]; //比之前搜到的最小的书号要小,朴素伐
}
}
if(flag) //不多解释了,输出
printf("%d
",minn);
else
printf("-1
");
}
return 0;
}好了下一题:
三、chess 棋盘
【题目描述】
有一个m × m的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1 个金币。
另外, 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
【输入输出格式】
输入格式:
数据的第一行包含两个正整数 m, n,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的 n 行,每行三个正整数 x, y, c, 分别表示坐标为( x, y)的格子有颜色 c。
其中 c=1 代表黄色, c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为( 1, 1),右下角的坐标为( m, m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是( 1, 1) 一定是有颜色的。
输出格式:
输出一行,一个整数,表示花费的金币的最小值,如果无法到达,输出-1。
输入输出样例
输入样例#1:
5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0
输出样例#1:
8
输入样例#2:
5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0
输出样例#2:
-1
【说明】
输入输出样例 1 说明
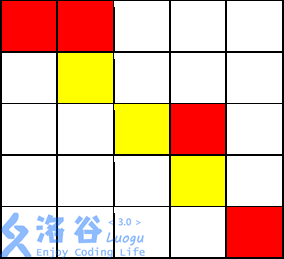
从( 1, 1)开始,走到( 1, 2)不花费金币
从( 1, 2)向下走到( 2, 2)花费 1 枚金币
从( 2, 2)施展魔法,将( 2, 3)变为黄色,花费 2 枚金币
从( 2, 2)走到( 2, 3)不花费金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)走到( 3, 4)花费 1 枚金币
从( 3, 4)走到( 4, 4)花费 1 枚金币
从( 4, 4)施展魔法,将( 4, 5)变为黄色,花费 2 枚金币,
从( 4, 4)走到( 4, 5)不花费金币
从( 4, 5)走到( 5, 5)花费 1 枚金币
共花费 8 枚金币。
输入输出样例 2 说明
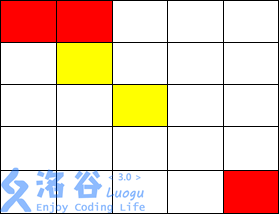
从( 1, 1)走到( 1, 2),不花费金币
从( 1, 2)走到( 2, 2),花费 1 金币
施展魔法将( 2, 3)变为黄色,并从( 2, 2)走到( 2, 3)花费 2 金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)只能施展魔法到达( 3, 2),( 2, 3),( 3, 4),( 4, 3)
而从以上四点均无法到达( 5, 5),故无法到达终点,输出-1
数据规模与约定
对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 10。
对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 200。
对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000。
【分析】
鄙人不才,考试的时候想不到什么法子,所以也就暴力深搜了!意外的是一个点都没爆(其实自己估摸的是不会超时的,更多担心的其实是栈溢出,内存不够这样子的,所以感谢强大的复赛评判系统吧,代码跟上)
【代码】
#include<bits/stdc++.h>
using namespace std;
int n,m,a[105][105],ans[105][105]; //a[i][j]是第i行j列的格子上的颜色,
//ans记忆到达该格子的最小金币数
int h[4]={-1,1,0,0},l[4]={0,0,-1,1}; //四个方向,上下左右
int read()
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-')
{
f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
return x*f;
}
void f(int x,int y,int mon,int used) //mon是当前已耗费金币数
//used记录在上一步有没有用过变颜色的魔法
{
for(int i=0;i<4;++i)
{
int xx=x+h[i],yy=y+l[i]; //为了下面不要那么烦,这里就先将--
//要去的格子位置记录为xx,yy了
if(!a[xx][yy]) //没颜色的时候
{
if(used && ans[xx][yy]>mon+2) //后面的判断是剪枝用的(下同 )
{
ans[xx][yy]=mon+2;
a[xx][yy]=a[x][y]; //无论如何,颜色先如题意变了吧,反正再不济后面也会剪枝剪掉的
f(xx,yy,mon+2,0); //继续深搜... (下同)
a[xx][yy]=0;
}
}
else if(a[xx][yy]==a[x][y]) //要去的格子与当前各自颜色相同
//(不用担心是没颜色的,刚刚不已经判断过了吗?好吧其实比赛的时候这里卡了一小会儿)
{
if(ans[xx][yy]>mon)
{
ans[xx][yy]=mon;
f(xx,yy,mon,1);
}
}
else
{
if(ans[xx][yy]>mon+1)
{
ans[xx][yy]=mon+1;
f(xx,yy,mon+1,1);
}
}
}
}
int main()
{
m=read();
if(m==1) //特判一下,1*1的棋盘就不用走了,直接输出完事儿嘛
{
cout<<0<<endl;
return 0;
}
n=read();
for(int i=0;i<n;++i)
{
int x,y,s;
x=read();
y=read();
s=read();
a[x][y]=s+1; //为什么加1?当然是为了规避颜色号“0”与初始值重复!
}
memset(ans,127,sizeof(ans));//初始化一下,注意不要把127改成128!
//这和原、反、补码知识有关,这里不再细谈,详情就百度补码之类的知识吧!
ans[1][1]=0;
ans[m][m]=5000000;
f(1,1,0,1); //开始深搜
if(ans[m][m]==5000000) //看看终点的金币是不是没变过,
//另外放心,根据题意金币值是达不到5000000的,貌似连2000000都达不到
{
printf("-1
");
return 0;
}
else
printf("%d
",ans[m][m]);
return 0;
}
好了,话不多说,t4吧!
四、jump 跳房子
ps:这道题的话,我只能说:I’m learing!不过大体思路还可以吧,所以借鉴一下别人的满分题解(刚用这个程序测的时候有个点爆了,WA,还没分析),再放个50分(我的)代码,到时候来改进啦!
【题目描述】
跳房子,也叫跳飞机,是一种世界性的儿童游戏,也是中国民间传统的体育游戏之一。
跳房子的游戏规则如下:
在地面上确定一个起点,然后在起点右侧画 n 个格子,这些格子都在同一条直线上。每个格子内有一个数字( 整数),表示到达这个格子能得到的分数。玩家第一次从起点开始向右跳, 跳到起点右侧的一个格子内。第二次再从当前位置继续向右跳,依此类推。规则规定:
玩家每次都必须跳到当前位置右侧的一个格子内。玩家可以在任意时刻结束游戏,获得的分数为曾经到达过的格子中的数字之和。
现在小 R 研发了一款弹跳机器人来参加这个游戏。但是这个机器人有一个非常严重的缺陷,它每次向右弹跳的距离只能为固定的 d。小 R 希望改进他的机器人,如果他花 g 个金币改进他的机器人,那么他的机器人灵活性就能增加 g, 但是需要注意的是,每次弹跳的距离至少为 1。 具体而言, 当g < d时, 他的机器人每次可以选择向右弹跳的距离为 d-g, d-g+1,d-g+2, …, d+g-2, d+g-1, d+g; 否则( 当g ≥ d时),他的机器人每次可以选择向右弹跳的距离为 1, 2, 3, …, d+g-2, d+g-1, d+g。
现在小 R 希望获得至少 k 分,请问他至少要花多少金币来改造他的机器人。
【输入输出格式】
输入格式:
第一行三个正整数 n, d, k, 分别表示格子的数目, 改进前机器人弹跳的固定距离, 以及希望至少获得的分数。 相邻两个数之间用一个空格隔开。
接下来 n 行,每行两个正整数x_i, s_i,分别表示起点到第i个格子的距离以及第i个格子的分数。 两个数之间用一个空格隔开。 保证x_i按递增顺序输入。
输出格式:
共一行,一个整数,表示至少要花多少金币来改造他的机器人。若无论如何他都无法获得至少 k 分,输出-1。
【输入输出样例】
输入样例#1:
7 4 10
2 6
5 -3
10 3
11 -3
13 1
17 6
20 2
输出样例#1:
2
输入样例#2:
7 4 20
2 6
5 -3
10 3
11 -3
13 1
17 6
20 2
输出样例#2:
-1
【说明】
输入输出样例 1 说明
花费 2 个金币改进后, 小 R 的机器人依次选择的向右弹跳的距离分别为 2, 3, 5, 3, 4,3, 先后到达的位置分别为 2, 5, 10, 13, 17, 20, 对应 1, 2, 3, 5, 6, 7 这 6 个格子。这些格子中的数字之和 15 即为小 R 获得的分数。
输入输出样例 2 说明
由于样例中 7 个格子组合的最大可能数字之和只有 18 ,无论如何都无法获得 20 分
数据规模与约定
本题共 10 组测试数据,每组数据 10 分。
对于全部的数据满足1 ≤ n ≤ 500000, 1 ≤ d ≤2000, 1 ≤ x_i, k ≤ 109, |si| < 105。 对于第 1, 2 组测试数据, n ≤ 10;
对于第 3, 4, 5 组测试数据, n ≤ 500
对于第 6, 7, 8 组测试数据, d = 1
【分析】
单调队列嘛,可以用二分。(之前测完之后发现5个点爆然后慌了,莫名其妙感觉二分错的。。。现在想想其实二分的方法是对的啦)
说了二分的话,其实小伙伴们应该也多有点思路了,二分哪个变量啊?当然是要花的金币k啦!多的话就在代码里谈吧。
【代码】
(1)
别人的代码(看了一下,和我的思路差不多,竟然大体思路一样!应该是我的程序哪儿有问题):
#include<deque>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
int x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
//这个判断数字的方法还是我的简单点...
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
return x*f;
}
#define MAXN 500000
int pos[MAXN+5],num[MAXN+5];
int N,D,K;
int f[MAXN+5];
/* 此模块中皆为原作者注释 */
bool dp_check(int g)
{
deque<int> Q;
memset(f,0,sizeof f);
int Lg=max(1,D-g),Rg=D+g;
int Now=0;//Now为现在新加入Q的格子
//printf("%d
",g);
for(int i=1;i<=N;i++)
{
while(pos[Now]+Lg<=pos[i])
{
while(!Q.empty()&&f[Q.back()]<=f[Now])
//注意,!Q.empty一定要写在前面
Q.pop_back();
Q.push_back(Now++);//不一定只放一个
}
while(!Q.empty()&&pos[Q.front()]+Rg<pos[i])//把队列前面不需要的pop掉
Q.pop_front();
if(!Q.empty()) f[i]=f[Q.front()]+num[i];//直接取出最前面的
else f[i]=-0x3f3f3f3f;//否则表示到不了这个格子
//printf(" %d
",f[i]);
if(f[i]>=K) return 1;//随时都有可能>=K,而不是只在循环完后比较f[N]与K
}
return 0;
}
int main()
{
N=read(),D=read(),K=read();
long long sum=0;
for(int i=1;i<=N;i++)
{
pos[i]=read(),num[i]=read();
if(num[i]>0) sum+=num[i];
}
if(sum<K) //挪,也是先特判...
{
printf("-1");
return 0;
}
int left=0,right=pos[N]; //pos[N],最右边的位置
while(left<right) //二分嘛,和我的差不多,--原文是"<",此处已改"<="
{
int mid=(left+right)>>1;//位运算优化(怎么又和我的这么像...)
if(dp_check(mid)) right=mid;
else left=mid+1;//mid也不符合条件,所以是mid+1
}
printf("%d",right);
}(2)
这是我的代码,刚订正了然后…runtime error 爆0了,算了,明天再订正吧!
#include<bits/stdc++.h>
#define M 5000005
using namespace std;
int n,d,k,l,r;
int x[M],s[M],ans[M],c[M],used[M];
int read()
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-')
{
f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
return x*f;
}
int check(int mid)
{
int head=0,tail=1,maxx=0;
memset(ans,128,sizeof(ans));
memset(used,0,sizeof(used));
ans[0]=0;
c[head]=0;
while(head<=tail)
{
for(int i=c[head]+1;i<=n;++i)
{
if(x[i]-x[c[head]]>mid+d) break;
if(x[i]-x[c[head]]<d-mid) continue;
if(!used[i])
{
c[tail++]=i;
used[i]=1;
}
if(ans[i]<ans[c[head]]+s[i])
{
ans[i]=ans[c[head]]+s[i];
if(ans[i]>maxx) maxx=ans[i];
}
}
head++;
}
// cout<<mid<<":"<<endl; //自己测试的时候的习惯
//
// for(int i=0;i<n;++i)
// printf("%4d ",x[i]);
// printf("
");
// for(int i=0;i<n;++i)
// printf("%4d ",s[i]);
// printf("
");
// for(int i=0;i<n;++i)
// printf("%4d ",ans[i]%100);
// printf("
");
return maxx;
}
int main()
{
n=read();
d=read();
k=read();
int tot=0;
for(int i=1;i<=n;++i)
{
x[i]=read();
s[i]=read();
if(s[i]>0) tot+=s[i];
}
if(tot<k)
{
printf("-1
");
return 0;
}
r=x[n];
int mid;
while(l<=r)
{
mid=(l+r)>>1;
if(check(mid)>=k) r=mid-1;
else l=mid+1;
}
printf("%d
",l);
return 0;
}
然后就是说好的订正了,还是90分,搞不出什么鬼来了,最后一个点就是爆。。。
代码如下:
#include<bits/stdc++.h>
typedef long long ll;
#define M 1000005
using namespace std;
ll n,d,k,l,r=1000000005;
ll ans=-1;
ll far[M],val[M],f[M];
ll read()
{
char c=getchar(); ll x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-') { f=-1; c=getchar(); }
while(isdigit(c)) { x=(x<<3)+(x<<1)+c-'0'; c=getchar(); }
return x*f;
}
ll check(ll g)
{
memset(f,-1,sizeof(f)); f[0]=0; //f(除f[0]外)全部赋值为-1
int q[M],head=1,tail=0,p=0;q[head]=0;
// q不用开很大,因为事实上队列中也就是每个点进一遍
for(int i=1;i<=n;++i)
{
while(far[i]-far[p]>=max(d-g ,(ll) 1) && p<i)
{ while(f[q[tail]]<=f[p] && head<=tail) --tail; q[++tail]=p++;}
//这里还是有点难理解的,其实也就是在i点之前的最优情况了,
//如果说队尾元素的f值要小于p点的f(注意队尾元素一定是p点之前的格子),
//那么就删去队尾元素,知道有更优的f。
//另外,因为这里的距离是单调的,所以就算q点跳不到i点,
//q点之前的点也一样调不到i点,何况更大的while语句里面有限制条件:
//p点和i点的距离不会小于可以跳的范围
while(far[i]-far[q[head]]>d+g && head<=tail) ++head;
//超距离了的点直接pass,况且后面也不会用到(单调了,后面的点肯定离这个点更远)
if(head>tail || f[q[head]]==-1) continue;
f[i]=f[q[head]]+val[i];
if(f[i]>=k) return true;
}
/* //这是原本的队列(已优化)
while(!Q.empty())
{
int now=Q.front();Q.pop();used[now]=0;
int i=now+1; while(far[i]-far[now]<max(d-mid , 1)) ++i;
for(;i<=n && far[i]-far[now]<=d+mid;++i)
{
if(!used[i]) //没有入队就入队
{ Q.push(i); used[i]=1; }
f[i]=max(f[i] , f[now]+val[i]);
}
}
*/
return false;
}
int main() //主程序还是挺简洁的,差不多就一个读入和二分查找
{
n=read(); d=read(); k=read();
for(int i=1;i<=n;++i)
{ far[i]=read(); val[i]=read(); }
ll mid;
while(l<=r)
{
mid=(l+r)>>1;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld
",ans);
return 0;
}好了,本文正式结束,喜欢请点赞!_ (:зゝ∠) _