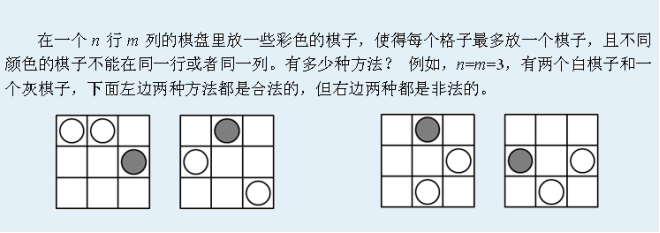
题目描述:
输入格式
输出格式
样例
数据范围与提示
solution:10%:cout<<0<<endl;
肯定有0的情况比如c>min(n,m)之类的。。。
20%:搜索,枚举所有状态。
据说这是搜索最高得分,然而博主考试时只拿到10分,而且还不是TLE。
下面说正解
我们考虑dp,设f[i][j][k]表示前k种颜色的棋子占领任意i行j列的方案数,g[i][j][k]表示第k种颜色的所有棋子占领任意i行j列的方案数;
那么我们首先可以得到g[i][j][k]=$C_{i*j}^{num[k]}$-$sum_limits{p=1}^{i}$$sum_limits{q=1}^{j}$g[p][q][k]*$C_{i}^{p}$*$C_{j}^{q}$
其实就是用合法的减去不合法的(实际上有没有被占领的行或列的方案数)
接下来得到f的方程:
$f[i][j][k]=sum_{p=0}^{i-1}sum_{q=0}^{j-1}$
$f[i][j][k]=sum_{p=0}^{i-1}sum_{q=0}^{j-1}f[p][q][k-1]*g[i-p][j-q][k]*C_{n-p}^{i-p}*C_{m-q}^{j-q}$,f[0][0][0]=1;
p,q,k-1就是枚举的上一个状态,$C_{n-p}^{i-p}$表示n-p行中选出i-p行放棋子,$C_{m-q}^{i-q}$同理,
最后ans=$sum_{i=1}^{n}$$sum_{j=1}^{m}$f[i][j][c],于是这道题就完美地解决了
放代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define mod 1000000009 5 #define ll long long 6 #define MAXNM 905 7 using namespace std; 8 int n,m,c,num[12]; 9 ll C[MAXNM][MAXNM],g[35][35][12],f[35][35][15],ans=0; 10 int main(){ 11 scanf("%d%d%d",&n,&m,&c); 12 for(int i=0;i<=n*m;i++){ 13 C[i][0]=1; 14 for(int j=1;j<=i;j++) 15 C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; 16 } 17 f[0][0][0]=1; 18 for(int k=1;k<=c;k++) 19 scanf("%d",&num[k]); 20 for(int k=1;k<=c;k++){ 21 for(int i=1;i<=n;i++) 22 for(int j=1;j<=m;j++){ 23 if(i*j<num[k]) continue; 24 g[i][j][k]=C[i*j][num[k]]; 25 for(int p=1;p<=i;p++) 26 for(int q=1;q<=j;q++){ 27 if(p<i||q<j) 28 g[i][j][k]=(g[i][j][k]-g[p][q][k]*C[i][p]%mod*C[j][q]%mod)%mod; 29 //cout<<g[i][j]<<endl; 30 } 31 } 32 } 33 for(int k=1;k<=c;k++){ 34 for(int i=1;i<=n;i++) 35 for(int j=1;j<=m;j++) 36 for(int p=0;p<i;p++) 37 for(int q=0;q<j;q++){ 38 int l=i-p,r=j-q; 39 if(l*r<num[k]) continue; 40 f[i][j][k]=(f[i][j][k]+f[p][q][k-1]*g[l][r][k]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod; 41 //cout<<f[i][j][k]<<endl; 42 } 43 } 44 for(int i=1;i<=n;i++) 45 for(int j=1;j<=m;j++) 46 ans=(ans+f[i][j][c])%mod; 47 printf("%lld ",ans); 48 return 0; 49 }
我们发现g只对当前一种棋子有贡献,所以第三维可以干掉,在每次输入时处理g和f
#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 1000000009
#define ll long long
#define MAXNM 905
using namespace std;
int n,m,c,num[12];
ll C[MAXNM][MAXNM],g[35][35],f[35][35][15],ans=0;
int main(){
scanf("%d%d%d",&n,&m,&c);
for(int i=0;i<=n*m;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
f[0][0][0]=1;
for(int k=1;k<=c;k++){
scanf("%d",&num[k]);
memset(g,0,sizeof(g));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(i*j<num[k]) continue;
g[i][j]=C[i*j][num[k]];
for(int p=1;p<=i;p++)
for(int q=1;q<=j;q++){
if(p<i||q<j)
g[i][j]=(g[i][j]-g[p][q]*C[i][p]%mod*C[j][q]%mod)%mod;
//cout<<g[i][j]<<endl;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int p=0;p<i;p++)
for(int q=0;q<j;q++){
int l=i-p,r=j-q;
if(l*r<num[k]) continue;
f[i][j][k]=(f[i][j][k]+f[p][q][k-1]*g[l][r]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod;
//cout<<f[i][j][k]<<endl;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans=(ans+f[i][j][c])%mod;
printf("%lld
",ans);
return 0;
}
