树的基本概念和常用术语
- 节点的度:一个结点的儿子结点个数称为该节点的度
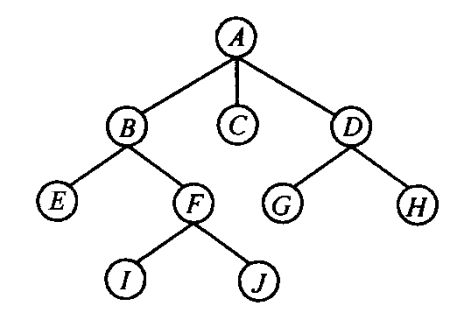
- 树的度:一棵树的度是指该树中结点的最大度数。如上图的树的度是3
- 叶节点或终端节点:度为零的节点。如上图中E,I,J,C,G,H是叶节点
- 非终端节点或分支节点:度不为零的节点。除根节点外的分支节点都叫做内部节点。
- 路径:若存在树中的一个节点序列k1,k2,…,kj,使得结点ki是ki+1的父结点(1<=i<j),则称该结点序列是树中从结点k1到结点kj的一条路径。
-
路径长度:路径所经过的边的数目。
-
节点高度:从该结点到各叶结点的最长路径长度,例如上图中B,C,D的高度分别是2,0,1
-
树的高度:(这里规定单根的高度为0)根结点的高度
-
结点的深度(或层数):从树根到任一结点n有唯一的路径,称该路径的长度为结点n的深度(或层数)。从根结点算起,根为第0层,它的孩子为第1层……
-
森林:m(m>=0)棵互不相交的树的集合
树的遍历
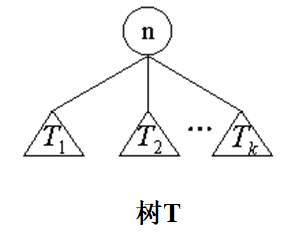
- 前序遍历:先访问树根n,然后依次前序遍历T1,T2,…,Tk。
- 中序遍历:先中序遍历T1,然后访问树根n,接着依次对T2,T3,…,Tk 进行中序遍历。
- 后序遍历:先依次对T1,T2,…,Tk进行后序遍历,最后访问树根n。
树的表示方法
- 父节点数组表示法

(1)树中的结点数字化为它们的编号1,2,…,n。
(2)用一个一维数组存储每个结点的父结点。即:father[k]中是存放结点k的父结点的编号。
(3)由于树中每个结点的父结点是唯一的,所以父结点数组表示法可以唯一表示任何一棵树。
- 儿子链表表示法
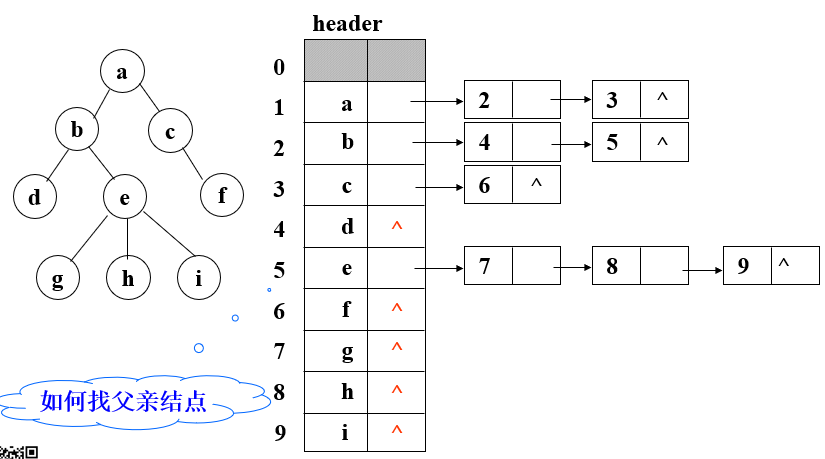
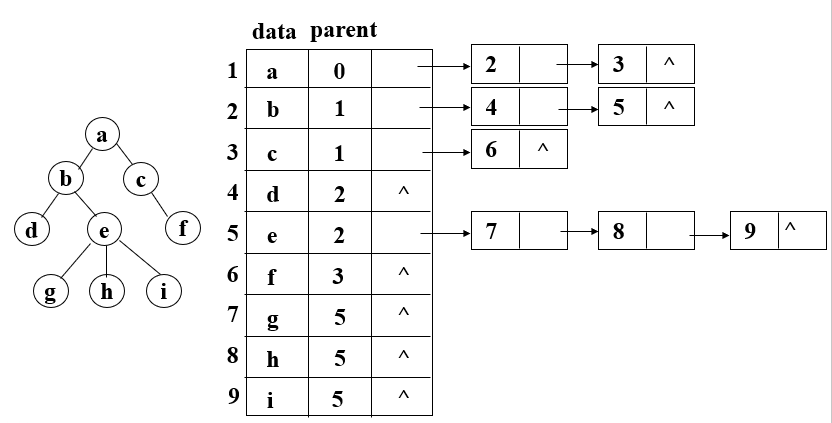
如果要查找父节点,可以再数组中添加一个parent域,用来存储每个节点的父节点对应数组下标。如下图:
- 左儿子兄弟表示法
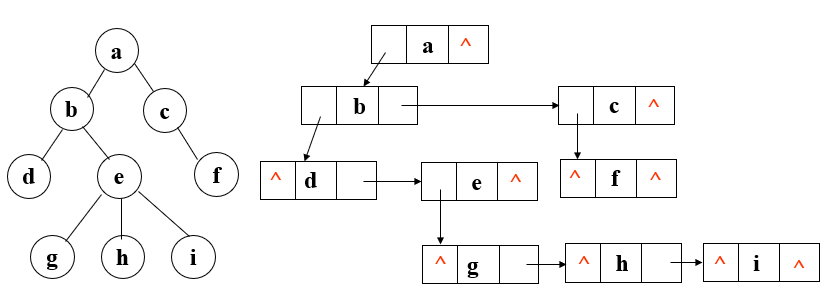
实现:用二叉链表作树的存储结构,链表中每个结点的两个指针域分别指向其最左儿子和右邻兄弟