广度优先遍历(BFS)
- 过程分析
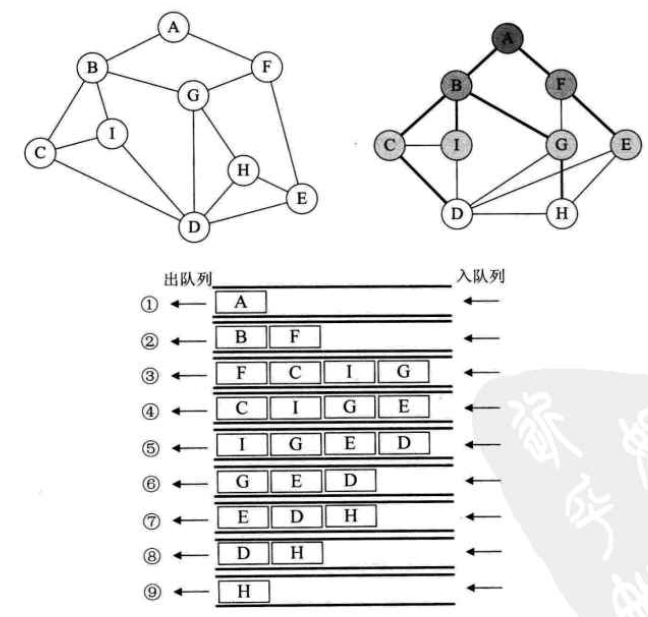
- 初始化一个队列。访问A顶点,将A顶点入队,之后出队。同时将与A顶点相邻接的顶点B,F入队
-
访问B结点,将B结点出队,同时将与B结点相邻接,且还未被访问过的顶点C,I,G入队
- 访问F结点,将F结点出队,同时将于F结点相邻接,且还未被访问过的顶点G,E入队。之后同理,直到队列为空。所得的出队序列就是遍历序列
- BFS代码
-
1 bool visited[MaxVertexNum]; //访问标记数组 2 //邻接矩阵的广度遍历算法 3 void BFSTraverse(MGraph G) 4 { 5 Queue Q; //辅助队列 6 for (int i = 0; i < G.vexnum; i++) 7 { 8 visited[i] = false; //访问标记数组初始化 9 } 10 InitQueue(Q); //初始化辅助队列 11 for (int i = 0; i < G.vexnum; i++) //从0号顶点开始遍历 12 if (!visited[i]) //对每个连通分量调用一次BFS 13 BFS(G, i); //Vi未访问过,从Vi开始BFS 14 } 15 16 void BFS(MGraph G, int v) 17 { 18 //从顶点v出发,广度优先遍历图G,算法借助一个辅助队列Q 19 visit(v); //访问结点v 20 visited[v] = true; //对v做访问标记 21 Enqueue(Q, v); //顶点v入队列 22 while (!isEmpty(Q)) 23 { 24 Dequeue(Q, v); //顶点v出队 25 for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))//检测v所有的邻接点 26 { 27 if (!visited[w]) //w为v还未访问过的邻接结点 28 { 29 visit(w); //访问顶点w 30 visited[w] = true; //对顶点w做访问标记 31 Enqueue(Q, w); //将顶点w入队 32 } 33 } 34 } 35 }
-
深度优先遍历(DFS)
- 过程分析:首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点w1,再访问与w1邻接且未被访问的任一顶点w2,....重复上述过程。当不能再继续访问的时候,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该顶点开始继续上述搜索过程,直到图中所有顶点均被访问过为止。
- DFS代码
-
1 /*深度优先遍历算法*/ 2 bool visited[MaxVertexNum]; //访问标记数组 3 void DFSTraverse(MGraph G) 4 { 5 for (int v = 0; v < G.vexnum; ++v) 6 visited[v] = false; //初始化访问标记数组 7 for (int v = 0; v < G.vexnum; ++v) //从顶点0开始遍历 8 { 9 if (!visited[v]) //顶点v还问访问过,则访问 10 DFS(G, v); 11 } 12 } 13 14 void DFS(MGraph G, int v) 15 { 16 //从顶点v出发,采用递归思想,深度优先遍历图 17 visit(v); 18 visited[v] = true; 19 for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))//检测v所有的邻接点 20 if (!visited[w]) 21 { 22 DFS(G, w); 23 } 24 }
-