计量经济学_一元线性回归_随机误差项

之前证明了整个回归方程,或者说梯度下降法的表达式, 现在来看看计量经济学里的回归表达式

y=ax+b, 出于对关系的不确定, 在计量经济学里,式子多了一个u作为随机干扰项

干扰项  u 我们认为是不可观测的值 

我自己的理解是这样_不是很严谨的粗糙理解:

 y=ax+b+u,我们改写成 y-u=ax+b, 发现u,y相对于x有同样的地位, 

也就是说,我们可以假设, y=ax+b+u, u=a1x+b1,

此时a1,b1是未知的,且无法求取的,因为干扰项  u 我们认为是不可观测的值,可以认为是无规律的

即y=ax+b+u=(a+a1)x+(b+b1),

a1会影响x对y的边际效应/斜率,a+a1, b1会影响截距项

a1,b1又无法观测所以, 那就不能只通过调整截距项来实现回归,

如果能通过调整截距项来实现, 必然, a1,b1=0; 即E(u)=0

教材的理解是这样:

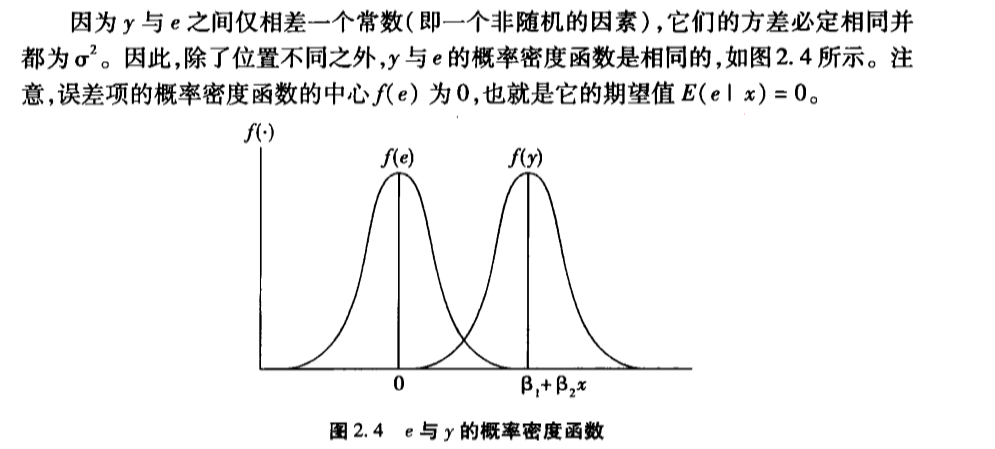
这里就是说的y和e有等价地位, 回归如果成立,那么E(e|x)=0

由于x为样本,实际值,可观测值,可以视为已知常数,则又有E(e)=0;

另外,百度百科里的解释也很好,

 这里有详细的证明解释

(random errorterm)随机误差项,常用缩写e表示

教材引用

 国外的教材真的平易近人....