Test on 11/4/2018

来浙理的第一次月赛，嗯我是被大佬吊着打的垃圾。

A：优美数

Description

如果一个数中只有少于三个数字是非零的，那么我们称这个数为优美数，我们定义这个优美数的优美程度为这个数所有数字相加的和。 例如优美数有4，200000，10203，其中4的优美度是4，200000的优美度是2，10203的优美度是6. 数字4231，102306，7277420000，就不是啰。

现在问在【L，R】中，有多少个优美度为x的优美数。

Input

T组数据，T<=5e4. 第一行为组数T。 接下来T行，每组输入L，R，x。1<=L <= R <= 3e18;

Output

每行输出一个对应的答案

Examples

Input

4

1 1000 1

1024 1024 7

65536 65536 15

1 1000000000 20

Output

4

1

0

3024

 

正确解法：

先dfs，预处理所有的情况，然后对每次询问进行二分求解。

也可用数位DP。

#include <algorithm>
#include  <iterator>
#include  <iostream>
#include   <cstring>
#include   <cstdlib>
#include   <iomanip>
#include    <bitset>
#include    <cctype>
#include    <cstdio>
#include    <string>
#include    <vector>
#include     <stack>
#include     <cmath>
#include     <queue>
#include      <list>
#include       <map>
#include       <set>
#include   <cassert>
using namespace std;
 
 
typedef long long ll;
 
            const int maxn = 3e6+9;
            int tot = 0;
            vector<ll>mp[30];
            int cnt(ll x){
                int res = 0;
                while(x>0){
                    res += x%10;
                    x/=10;
                }
                return res;
            }
            set<int>sss;
            void dfs(ll x,int cur,int num){
                if(cur>19||num > 3)return;
 
                if(num<=3){
                    int tmp = cnt(x);
                    mp[tmp].pb(x);
                    // tot++;
                    sss.insert(tmp);
                    // if(cnt(x) == 50)cout<<x<<endl;
                }
                for(int i=0;i<=9; i++){
                    if(i==0)dfs(x*10ll, cur+1,num);
                    else dfs(x*10ll + i, cur+1,num+1);
                }
            }
            int find1(ll x,int id){
                int le = 0,ri = mp[id].size() - 1;
                int res = ri+1;
                while(le <= ri){
                    int mid = (le + ri)>>1;
                    
                    if(mp[id][mid] < x){
                        le = mid+1;
                    }
                    else{
                        res = mid; ri = mid - 1;
                    }
                }
 
                return res;
            }
             int find2(ll x,int id){
                int le = 0,ri = mp[id].size() - 1;
                int res = 0;
                while(le <= ri){
                    int mid = (le + ri)>>1;
                    if(mp[id][mid] > x){
                        ri = mid - 1;
                    }
                    else {
                        res = mid;
                        le = mid + 1;
                    }
                }
                return res;
            }
int main(){
 
            // freopen("data.in","r", stdin);
            // freopen("output.out","w",stdout);
            for(int i=1; i<=9; i++)dfs(i,1,1);
            //tot = 720423
    
            for(int k : sss){//27次
                sort(mp[k].begin(),mp[k].end());
            }
 
            int t;scanf("%d", &t);
            while(t--){
                ll l,r;int x;
                scanf("%lld%lld%d", &l, &r, &x);
                if(x >= 28){
                    puts("0");
                }
                else if(l<r){
                        int t1 = find1(l,x);
                        int t2 = find2(r,x);
                        printf("%d
",t2 - t1 + 1);
                }
                else if(l==r){
                        int t1 = lower_bound(mp[x].begin(),mp[x].end(),l) - mp[x].begin();
                        if(t1<mp[x].size() && mp[x][t1] == l)puts("1");
                        else puts("0");
                }
            }
           return 0;
}

#include <algorithm>
#include  <iterator>
#include  <iostream>
#include   <cstring>
#include   <cstdlib>
#include   <iomanip>
#include    <bitset>
#include    <cctype>
#include    <cstdio>
#include    <string>
#include    <vector>
#include     <stack>
#include     <cmath>
#include     <queue>
#include      <list>
#include       <map>
#include       <set>
#include   <cassert>
using namespace std;
#define se second
#define fi first
#define ll long long
#define Pii pair<int,int>
#define Pli pair<ll,int>
#define ull unsigned long long
#define pb push_back
const int N=1e4+10;
const int INF=0x3f3f3f3f;
const int mod=1e9+7;
using namespace std;
int a[30];
ll dp[20][30][4][30];
int k;
ll dfs(int pos,int now,int num,bool limit){
    if(num > 3) return 0;
    if(pos==-1) return now == k;
    if(!limit && dp[pos][now][num][k]!=-1) return dp[pos][now][num][k];
    int up=limit?a[pos]:9;
    ll ans=0;
    for(int i=0;i<=up&&now+i<=k;++i){
       ans+=dfs(pos-1,now+i,num+(i!=0),limit&&i==a[pos]);
    }
    if(!limit) dp[pos][now][num][k]=ans;
    return ans;
}
ll solve(ll x){
    int pos=0;
    if(x==0)return 0;
    while(x){
        a[pos++]=x%10;
        x/=10;
    }
    return dfs(pos-1,0,0,1);
}
int main(){
//    freopen("data1.in", "r", stdin);
//    freopen("ac.out", "w", stdout);
    memset(dp,-1,sizeof(dp));
 
    int T;scanf("%d",&T);
    while(T--){
        ll l,r;
        scanf("%I64d%I64d%d",&l,&r,&k);
        if(k>27)printf("0
");
        else printf("%I64d
",solve(r)-solve(l-1));
    }
 
    return 0;
}

B：私人奶茶店

Description

小C有一家奶茶店，其中有n种奶茶，每种奶茶都有a【i】个，小C每天都会等概率地从剩余的奶茶中选一杯奶茶喝掉，问小C第K天喝到第m种奶茶的概率是多少。

Input

第一行n，代表奶茶的种类数

第二行n个数，表示a【i】

第三行k，m，表示第k天喝到第m种奶茶的概率

（n<=1e5, 0 < a[i] <= 1e6）

（1<=k<=sum(a[i]), 1<=m<=n）

Output

用最简分数表示。

Examples

Input

2

1 1

1 1

Output

1/2

正确解法：

a[m] / sum   与k无关，最后要gcd

#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 1e5+9;
ll a[maxn];
ll gcd(ll a, ll b){
    if(b==0)return a;
    return gcd(b, a%b);
}
int main(){ 
        // freopen("data5.in", "r", stdin);
        int n;scanf("%d", &n);
        ll sum = 0;
        for(int i=1; i<=n; i++)scanf("%lld", &a[i]),sum+=a[i];
        cout<<"sum"<<sum<<endl;
        int k,m;
        scanf("%d%d", &k, &m);
        ll g = gcd(sum,a[m]);
        printf("%lld/%lld
", 1ll*a[m]/g, 1ll*sum/g);
        return 0;
}

C:素数空间

Description

一天，小明正在搬砖，他收集了n（n<=1e7）种砖，砖的编号1-n这个时候，他突然说了一句，召唤神龙，然后，他穿越到了一个时空，发现这里的东西都是由素数组成的，这里的砖也和素数有关，他的砖也和他一块过来了，只是发生了一些变化，编号为1的砖不见了，编号为素数的砖没有发生变化，编号为合数的砖变成了编号为几块素数的砖(砖的编号和为之前的那个合数)，由于这个世界能量太少，所以这些合数的砖尽可能的变成数目少的其他砖。于是小明想请教你他还有多少砖。例如 编号为12的砖会变成编号5 7 的砖  不会变成编号2 3 2 2 3 的砖     编号9的砖会变成编号2 7 的砖  不会变成编号 3 3 3  的砖

Input

给你一个T（1<=T<=3e3） 

接下来T行每行一个n(0<=n<=1e7)

Output

一共T行，每一行输出一个结果；

Examples

Input

2

3

5

Output

2

5

正确解法：

根据哥德巴赫猜想：

大于二的偶数可以分解为两个素数之和

大于七的奇数可以分解为三个素数之和

（一定可以分解成三个素数之和，也有可能分解为两个，分解成两个其中必然有一个是2，其他就是至少三个）

1.先线性筛出所有的素数。

2.遍历1-le7里的素数、偶合数、奇合数

3.预处理一遍就行了

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+5;
bool prime[maxn];
int p[maxn];
int tot;
void findprime()
{
    for(int i = 2; i < maxn; i ++)  prime[i] = true;
    for(int i = 2; i < maxn; i ++)
    {
        if(prime[i])  p[++tot]=i;
        for(int j=1;j<=tot && i*p[j]<maxn; j++)
        {
            prime[i*p[j]]=false;
            if(i%p[j]== 0) break;
        }
    }
}
int  ans[maxn];
int main()
{
   // freopen("g4.in","r",stdin);
   // freopen("g4.out","w",stdout);
    findprime();
    for(int i=2;i<=maxn;i++)
    {
        if(prime[i]==1) ans[i]=ans[i-1]+1;
        else
        {
            if(i%2==0) ans[i]=ans[i-1]+2;
            else
            {
                if(prime[i-2]==1) ans[i]=ans[i-1]+2;
                else              ans[i]=ans[i-1]+3;
            }
        }
    }
   int t;cin>>t;
   while(t--)
   {
       int n; cin>>n; cout<<ans[n]<<endl;
   }
}

D：摩天大楼

Description

随着科技的发展，某国家准备修建一座高楼，高度为n（n<=1e18），来展现他们国家的强大国力，他们国家有两支强大的施工队，国家于是把修建计划给了这两只施工队，为了提高施工队的积极性，国家会特殊奖励最后完成施工的，两只施工的施工计划是两只施工队轮流工作，由于施工队实力有限，每天只能修建1-m(m<=1e18)层，假如两只施工队都非常聪明，问首先施工的那只队伍能不能获得奖励，能输出YES，不能输出NO

Input

数据的组数 T；（T<=3000）     

接下来T行，每行一个n m, 楼的高度，最大修建层数   (n,m<=1e18)

Output

每行一个单独的YES或者NO；

Examples

Input

2

2 1

6 4

Output

NO

YES

正确解法：

两只队伍都非常聪明，知道如何使自己赢，每个人取的都是1~m个

无论第一支队伍取多少个，第二支队伍都能使两只队伍的和为1+m 个

故 n为m+1的倍数或者0时候，先手必输，其余先手必赢.

#include<bits/stdc++.h>
using namespace std;
int main()
{
   // freopen("cc.in","r",stdin);
  //  freopen("in.out","w",stdout);
    long long n,m;
    int t; cin>>t;
    while(t--)
    {
       cin>>n>>m;
      if(n%(m+1)==0) cout<<"NO"<<endl;
       else           cout<<"YES"<<endl;
    }
}

E：招生

Description

 浙江理工大学招生，一开始有0名学生报考，现在有如下几种情况；

1.增加一名报考学生，报考学生成绩为x；

2.一名成绩为x的学生放弃报考。

3.从现在报考的学生来看，老师想知道如果要招生至少x名学生，需要将分数线最高设置为多少；

4.从现在报考的学生来看，如果分数线设置为x，能有几名学生被录取。

第一行先输入一个n，表示有n次操作或查询；

接下来n行，每行输入两个整数opt和x（用空格隔开）：

如果opt为1，则增加一名报考学生，报考学生成绩为x；

如果opt为2，则表示一名成绩为x的学生放弃报考。

如果opt为3，从现在报考的学生来看，老师想知道如果要招生至少x名学生，需要将分数线最高设置为多少，输出最高分数线。

如果opt为4，从现在报考的学生来看，如果分数线设置为x，能有几名学生被录取，输出录取人数。

对于每个输出占一行。

n不超过50000；0<=x<=1000000;1<=k<=现在的学生数。

Input

第一行输入一个n，接下来n行，每行输出两个整数opt，x，用空格隔开

Output

对于每次输出， 输出一个整数占一行

Examples

Input

18

1 3

1 4

1 5

1 6

1 7

1 8

1 9

1 10

1 11

1 12

2 8

3 2

3 3

3 4

3 5

4 8

4 9

4 7

Output

11

10

9

7

4

4

5

正确解法：

平衡树treap

#include<bits/stdc++.h>
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define pqueue priority_queue
#define NEW(a,b) memset(a,b,sizeof(a))
const double pi=4.0*atan(1.0);
const double e=exp(1.0);
const int maxn=1e6+8;
typedef long long LL;
typedef unsigned long long ULL;
//typedef pair<LL,LL> P;
const LL mod=1e9+7;
const ULL base=1e7+7;
using namespace std;
struct node{
    int son[2];
    int siz;
    int key,w;
}a[maxn];
int tot=0;
int root=0,vis[maxn];
void up(int i){
    a[i].siz=a[a[i].son[0]].siz+a[a[i].son[1]].siz+1;
}
void Rotate(int &i,int d){
    int t=a[i].son[d];
    a[i].son[d]=a[t].son[!d];
    a[t].son[!d]=i;
    up(i);up(t);
    i=t;
}
void Insert(int &i,int key){
    if(i==0){
        i=++tot;
        a[i].siz=1;a[i].key=key;a[i].w=rand();
        return ;
    }
    a[i].siz++;
    if(a[i].key>=key) {
        Insert(a[i].son[0],key);
        if(a[a[i].son[0]].w<a[i].w) Rotate(i,0);
    }
    else{
        Insert(a[i].son[1],key);
        if(a[a[i].son[1]].w<a[i].w) Rotate(i,1);
    }
}
void Del(int &i,int key){
    if(a[i].key==key){
        if(a[i].son[0]*a[i].son[1]==0)  {i=a[i].son[0]+a[i].son[1];return ;}
        if(a[a[i].son[0]].w>a[a[i].son[1]].w){
            Rotate(i,1);
            Del(a[i].son[0],key);
        }
        else{
            Rotate(i,0);
            Del(a[i].son[1],key);
        }
    }
    else if(a[i].key>key){
        Del(a[i].son[0],key);
    }
    else{
        Del(a[i].son[1],key);
    }
    up(i);
}
int Find(int i,int key){
    if(i==0) return 1;
    if(a[i].key>=key) return Find(a[i].son[0],key);
    else return a[a[i].son[0]].siz+Find(a[i].son[1],key)+1;
}
int Search(int i,int rak){
    if(a[a[i].son[0]].siz==rak-1) return a[i].key;
    if(a[a[i].son[0]].siz>=rak) return Search(a[i].son[0],rak);
    else  return Search(a[i].son[1],rak-a[a[i].son[0]].siz-1);
}
int pre(int i,int key){
    if(i==0) return -10000008;
    if(a[i].key<key) return max(a[i].key,pre(a[i].son[1],key));
    return pre(a[i].son[0],key);
}
int bhe(int i,int key){
    if(i==0) return 10000008;
    if(a[i].key>key) return min(a[i].key,bhe(a[i].son[0],key));
    return bhe(a[i].son[1],key);
}
int main(){
    int n;
    freopen("data1.in","r",stdin);
    freopen("data1.out","w",stdout);
    scanf("%d",&n);
    int opt,x;
    int sum=0;
    while(n--){
        scanf("%d%d",&opt,&x);
        if(opt==1){
            Insert(root,x);
            sum++;
            vis[x]++;
        }
        if(opt==2){
            if(vis[x]){
                Del(root,x);
                sum--;
                vis[x]--;
            }
        }
        if(opt==3){
            printf("%d
",Search(root,sum-x+1));
        }
        if(opt==4){
            printf("%d
",sum-Find(root,x)+1);
        }
    }
}

F: 闲的无聊的简单题

Description

给你一个n*m的二维数组，a[i][j]表示第i行第j列的数字，现在求一个最大面积（长乘宽）的子矩形，要求对于该子矩形每一行中相邻的两个数，a[i][j]和a[i][j+1]，存在一个整数k使得2的k次方同时小于等于a[i][j]和a[i][j+1]，并且2的（k+1）次方大于a[i][j]和a[i][j+1]，对于每一列中相邻的两个数，a[i][j]和a[i+1][j]，不存在一个整数k使得2的k次方同时小于等于a[i][j]和a[i+1][j]，并且2的（k+1）次方大于a[i][j]和a[i+1][j]。（0<n，m<=500）。

Input

第一行输入两个数n，m

接下来n行，每行m个整数第i行第j列表示a[i][j]（0<a[i][j]<=1e9）

Output

输出一个表示符合要求的最大矩形面积

Examples

Input

4 4

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

Output

6

描述：

对于样例，面积为6的矩形如下
2 3
6 7
10 11

正确解法：

判断一个数a与另一个数b是否存在一个k满足可以用异或，令c=a^b，如果c同时小于a和b，则存在，否则则不存在。开三个数组up,l,r存每个点上边，左边和右边可以到达的最值，并且l和r不断更新，每次不断更新面积最大值即可。

 

#include<bits/stdc++.h>
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define pqueue priority_queue
#define NEW(a,b) memset(a,b,sizeof(a))
const double pi=4.0*atan(1.0);
const double e=exp(1.0);
const int maxn=1e6+8;
typedef long long LL;
typedef unsigned long long ULL;
const LL mod=1e9+7;
const ULL base=1e7+7;
using namespace std;
int a[2008][2008];
int l[2008][2008],r[2008][2008],u[2008][2008];
int main(){
    //freopen("data5.in","r",stdin);
    //freopen("data5.out","w",stdout);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
        }
        l[i][1]=1;r[i][m]=m;
        int k;
        for(int j=2;j<=m;j++){
            k=a[i][j]^a[i][j-1];
            if(a[i][j]>=k&&a[i][j-1]>=k){
                l[i][j]=l[i][j-1];
            }
            else{
                l[i][j]=j;
            }
        }
        for(int j=m-1;j>=1;j--){
            k=a[i][j]^a[i][j+1];
            if(a[i][j]>=k&&a[i][j+1]>=k){
                r[i][j]=r[i][j+1];
            }
            else{
                r[i][j]=j;
            }
        }
    }
    int maxa=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i>1&&(a[i][j]<(a[i][j]^a[i-1][j])||a[i-1][j]<(a[i][j]^a[i-1][j]))){
                u[i][j]=u[i-1][j]+1;
                l[i][j]=max(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
            }
            else{
                u[i][j]=1;
            }
            maxa=max(maxa,(r[i][j]-l[i][j]+1)*u[i][j]);
        }
    }
    //cout<<u[39][17]<<endl;
    cout<<maxa<<endl;
}

G: 简单题*10086

Description

现有N个数c1,c2,...,cN。对于每个数求有多少个有序二元组(i,j)满足以下式子   

ci * cj mod P=ck（i，j，k可想等）

其中P为一给定质数。对于每个k对应的答案记为cnt[k]，请你将每两个相邻的答案相加，这样答案总个数每次减少1，当答案个数为1时结束（结果对1e9+7取模）。为了感谢wjh、xxb、lmb、cly、ckx、yzj出了一堆简单题，请将他们名字缩写（小写）合并后去重并输出字典序第k大，k为所得结果乘上2333333后取模6666666的结果。

Input

第一行输入一个组数t（t ≤ 5）。

对于每组数据第一行有两个正整数N,P(1 ≤ N ≤ 100000，2 ≤ P ≤ 100000), P为质数。

第二行N个非负整数c1,c2,...,cN(0 ≤ ci ≤ 1e9)。

Output

输出共一行，为对应答案的字典序排列（答案为0输出-1）。

Examples

Input

2

7 3

1 2 3 4 5 6 7

5 7

1 0 2 3 0

Output

ckybhmwzxjl

byjlhwzmckx

正确解法：

例如答案是1 2 3 4 5那么你应该经过以下变化变成一个答案1 2 3 4 5 

3 5 7 9
8 12 16
20 28
48

 

我们令g为质数P的原根，那么对于一个数字ai，唯一存在一个数字bi，使得  。那么我们把所有的ai用这种形式表示，于是对于原本的式子ci*cj≡ck(mod P)，有，那么可以有bi+bj=bk。这样问题就从乘法变成了加法，FFT就可以排上用场了。而且你会发现，这里的bi的大小都是在P以内的。这样直接FFT即可，最后特殊处理一下0的情况即可。而对于接下来的一部可以发现最后结果就是C(n-1,0)*a[1]+C(n-1,1)*a[2]+……+C(n-1,n-1)*a[n]，可以O(n)求出答案，最后一步是个逆康托展开。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <bitset>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll inff = 0x3f3f3f3f3f3f3f3f;
#define FOR(i,a,b) for(int i(a);i<=(b);++i)
#define FOL(i,a,b) for(int i(a);i>=(b);--i)
#define REW(a,b) memset(a,b,sizeof(a))
#define inf int(0x3f3f3f3f)
#define si(a) scanf("%d",&a)
#define sl(a) scanf("%lld",&a)
#define sd(a) scanf("%lf",&a)
#define ss(a) scanf("%s",a)
#define mod ll(6666666)
#define pb push_back
#define eps 1e-6
#define lc d<<1
#define rc d<<1|1
#define Pll pair<ll,ll>
#define P pair<int,int>
#define pi acos(-1)
ll n,p,g,id[2000008],m,ans[5000008],pr[1000008],prime[1000008],qw[1000008],tot;
ll a[100008],jc[15],inv[100008],mm=1e9+7,vis[15],sss[100008];
char s[15],ss[5008];
inline int read()
{
    int X=0,w=0; char ch=0;
    while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
    while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
void init(int n)
{
    int i,j;
    tot=0;
    prime[1]=1;
    for(i=2;i<=n;i++)
    {
        if(!prime[i]) prime[i]=pr[tot++]=i;
        for(j=0;j<tot&&pr[j]*i<=n;j++)
        {
            prime[i*pr[j]]=pr[j];
            if(i%pr[j]==0) break;
        }
    }
}
ll gmod(ll a,ll b,ll p)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*a%p,b>>=1;
    }
    return res;
}
int root(int x)
{
    int f,phi=x-1;qw[0]=0;
    for(int i=0;phi&&i<tot;i++)
    {
        if(phi%pr[i]==0)
        {
            qw[++qw[0]]=pr[i];
            while(phi%pr[i]==0) phi/=pr[i];
        }
    }
    for(int g=2;g<=x-1;g++)
    {
        f=1;
        for(int i=1;i<=qw[0];i++)
         if(gmod(g,(x-1)/qw[i],x)==1) {f=0;break;}
        if(f) return g;
    }
    return 0;
}
struct CP{
    double x,y;
    CP(){} CP(double a,double b):x(a),y(b){}
    CP operator+(const CP&r) const{return CP(x+r.x,y+r.y);}
    CP operator-(const CP&r) const{return CP(x-r.x,y-r.y);}
    CP operator*(const CP&r) const{return CP(x*r.x-y*r.y,x*r.y+y*r.x);}
}b[5000008],t;
inline void Swap(CP&a,CP&b) {t=a;a=b;b=t;}
inline void fft(CP*a,int f,int n)
{
    int i,j,k;
    for(i=j=0;i<n;i++)
    {
        if(i>j) Swap(a[i],a[j]);
        for(k=n>>1;(j^=k)<k;k>>=1);
    }
    for(int i=1;i<n;i<<=1)
    {
        CP wn(cos(pi/i),f*sin(pi/i));
        for(int j=0;j<n;j+=i<<1)
        {
            CP w(1,0);
            for(int k=0;k<i;k++,w=w*wn)
            {
                CP x=a[j+k],y=w*a[i+j+k];
                a[j+k]=x+y;a[i+j+k]=x-y;
            }
        }
    }
    if(f==-1) FOR(i,0,n) a[i].x/=n;
}
void rkt(ll n,ll k)
{
    ll t,ty=0;
    REW(vis,0);
    n--;
    FOR(i,0,k-1)
    {
        t=n/jc[k-i-1];
        n%=jc[k-i-1];
        for(ll j=0,pos=0;;j++,pos++)
        {
            if(vis[pos]) j--;
            if(j==t){vis[pos]=1;s[ty++]=('a'+pos+1);break;}
        }
    }
}
int main()
{
    cin.tie(0);
    cout.tie(0);
    freopen("date1.in","r",stdin);
    freopen("date1.out","w",stdout);
    int tt;
    cin>>tt;
    ss['b']='b',ss['c']='c',ss['d']='h',ss['e']='j',ss['f']='k',ss['g']='l';
    ss['h']='m',ss['i']='w',ss['j']='x',ss['k']='y',ss['l']='z';
    jc[0]=jc[1]=1;
    for(ll i=2;i<=12;i++) jc[i]=jc[i-1]*i;
    inv[1]=1;
    FOR(i,2,100005)  inv[i]=(mm-mm/i)*inv[mm%i]%mm;
    init(100000);
    while(tt--)
    {
        cin>>n>>p;
        g=root(p);
        ll tmp=1,qw=0,er,sum=1;
        for(int i=1;i<p-1;i++)
        {
            tmp=tmp*g%p;
            id[tmp]=i;
        }
        er=m=p-1;
        for(m=er+m,er=1;er<=m;er<<=1);
        FOR(i,0,er+1) b[i].x=b[i].y=0.0,ans[i]=0;
        FOR(i,1,n)
        {
            a[i]=read();
            if(!(a[i]%p)) qw++;
            else b[id[a[i]%p]].x+=1.0;
        }
        fft(b,1,er);
        FOR(i,0,er) b[i]=b[i]*b[i];
        fft(b,-1,er);
        for(int i=0;i<2*p;i++) ans[i%(p-1)]+=(ll)(b[i].x+0.2);
        for(int i=1;i<=n;i++)
        {
            if(a[i]>=p) er=0;
            else if (a[i]==0) er=2*qw*n-qw*qw;
            else er=ans[id[a[i]]];
            sss[i]=er;
        }
        er=0;
        for(int i=0;i<n;i++)
        {
            er=(er+sum*sss[i+1])%mm;
            sum=(sum*(n-1-i)%mm)*inv[i+1]%mm;
        }
        //cout<<er<<endl;
        er=((er%mod)*2333333)%mod;
        if(er==0) {puts("-1");continue;}
        rkt(er,11);
        for(int i=0;i<11;i++) printf("%c",ss[s[i]]);
        puts("");
    }
    return 0;
}

 

H: 简单题*10000

Description

已知一排硬币中有n个硬币正面朝上，输入正面朝上的硬币的位置ai（可能重复）。

两人轮流操作，每次操作可以翻转1,2,或则3枚硬币（不一定连续），其中翻转的最右的硬币必须是正面朝上的，最后不能翻转的为负

Input

第一行输入一个组数t（t ≤ 100）。

对于每组数据第一行有一个正整数N(0 ≤ N ≤ 5000)。

第二行N个非负整数c1,c2,...,cN(0 ≤ ai ≤ 1e9)。

Output

如果先手必胜输出Yes，否则输出No。

Examples

Input

2

1

0

4

0 1 2 3

Output

Yes

No

正确解法：

定义硬币全反时的sg为0，现在单个游戏就是只有一枚硬币朝上，其余都是反，其他情况都可以由单一游戏组合而成。如果位置i有一个正面朝上的硬币，其余都是反，那么这枚硬币翻过来的时候，它可以到达的局面是1、sg = 0   2、sg(j)j位置的硬币朝上，其余都是反（j<i） 3、出现两个正面朝上的硬币，变成组合游戏sg(j)和sg(k)。我们把sg函数打表出来就可以找到规律。（hdu3537）

初始编号从0开始。

当N==1时，硬币为：正，先手必胜，所以sg[0]=1.

当N==2时，硬币为：反正，先手必赢，先手操作后可能为：反反或正反，方案数为2，所以sg[1]=2。

当N==3时，硬币为：反反正，先手必赢，先手操作后可能为：反反反、反正反、正反正、正正反，方案数为4，所以sg[2]=4。

位置x：0  1  2  3  4   5    6   7    8     9  10  11  12  13  14...

sg[x]：  1  2  4  7  8  11 13 14  16  19  21  22  25  26  28…

看上去sg值为2x或者2x+1。我们称一个非负整数为odious，当且仅当该数的二进制形式的1出现的次数是奇数，否则称作evil。所以1，2，4，7是odious因为它们的二进制形式是1,10,100,111.而0,3,5,6是evil，因为它们的二进制形式是0,11,101,110。而上面那个表中，貌似sg值都是odious数。所以当2x为odious时，sg值是2x，当2x是evil时，sg值是2x+1.

这样怎么证明呢？我们会发现发现，

                                                     evil^evil=odious^odious=evil

                                                     evil^odious=odious^evil=odious

假设刚才的假说是成立的，我们想证明下一个sg值为下一个odious数。注意到我们总能够在第x位置翻转硬币到达sg为0的情况；通过翻转第x位置的硬币和两个其它硬币，我们可以移动到所有较小的evil数，因为每个非零的evil数都可以由两个odious数异或得到；但是我们不能移动到下一个odious数，因为任何两个odious数的异或都是evil

假设在一个Mock Turtles游戏中的首正硬币位置x1,x2,…,xn是个P局面，即sg[x1]^…^sg[xn]=0.那么无可置疑的是n必定是偶数，因为奇数个odious数的异或是odious数，不可能等于0。而由上面可知sg[x]是2x或者2x+1，sg[x]又是偶数个，那么x1^x2^…^xn=0。相反，如果x1^x2^…^xn=0且n是偶数，那么sg[x1]^…^sg[xn]=0。这个如果不太理解的话，我们可以先这么看下。2x在二进制当中相当于把x全部左移一位，然后补零，比如说2的二进制是10，那么4的二进制就是100。而2x+1在二进制当中相当于把x全部左移一位，然后补1，比如说2的二进制是10，5的二进制是101。现在看下sg[x1]^…^sg[xn]=0，因为sg[x]是2x或者2x+1，所以式子中的2x+1必须是偶数个（因为2x的最后一位都是0,2x+1的最后一位都是1，要最后异或为0,2x+1必须出现偶数次）

 

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <bitset>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll inff = 0x3f3f3f3f3f3f3f3f;
#define FOR(i,a,b) for(int i(a);i<=(b);++i)
#define FOL(i,a,b) for(int i(a);i>=(b);--i)
#define REW(a,b) memset(a,b,sizeof(a))
#define inf int(0x3f3f3f3f)
#define si(a) scanf("%d",&a)
#define sl(a) scanf("%lld",&a)
#define sd(a) scanf("%lf",&a)
#define ss(a) scanf("%s",a)
#define mod ll(6666666)
#define pb push_back
#define eps 1e-6
#define lc d<<1
#define rc d<<1|1
#define Pll pair<ll,ll>
#define P pair<int,int>
#define pi acos(-1)
int n,a[100008];
int as(int x)
{
    int k=0;
    while (x)
    {
        if (x&1) k++;
        x>>=1;
    }
    return !(k&1);
}
int main()
{
    cin.tie(0);
    cout.tie(0);
    //freopen("game001.in","r",stdin);
    //freopen("game001.out","w",stdout);
    int tt;
    cin>>tt;
    while(tt--)
    {
        si(n);
        FOR(i,1,n) si(a[i]);
        sort(a+1,a+n+1);
        int k=unique(a+1,a+n+1)-a-1,s=0;
        FOR(i,1,k)
        {
            a[i]*=2ll;
            if(as(a[i])) a[i]++;
            s^=a[i];
        }
        if(s) puts("Yes");
        else puts("No");
    }
    return 0;
}

 

I: 水题

Description

史努比最爱水题了，他知道现在他要挑战的是一道超级大水题哦。不过因为太水了，而且他又很懒,所以把这道水题推给了你们。

有n个(不包括ZSTU和火车东站)车站介于ZSTU和火车东站之间，一共有m辆公交车往返于这些车站和火车东站。每个车站假设可以站无数个人，每辆车最多承载H[i]个人，经过S[i]个车站。假设一辆车依次经过1,2,3，这三个车站，那么它将一直往复1->2->3->1->2...现在认为车从一个站到下一个站要花费1个小时，人只能在车站或ZSTU,火车东站上下车，初始时有k个人在ZSTU（0站）,所有的车都在初始站（所给车站的第一个车站为初始站)，现在问你们最快让全部人从ZSTU到火车东站要多少小时。所有车同时运行。

Input

第一行有一个T<=10，表示T组测试样例，第二行三个数n(车站数目),m(车数目),k(人数)，(n<=13,m<=20,k<=50);接下来的m行给出车信息,每行给出H[i](能承载的最大人数),S[i](经过的车站数目),还有依次给出S[i]个车站编号。ZSTU用0编号表示，火车东站用-1表示。

Output

若无解则输出-1，否则逐行输出答案。

Examples

Input

2

2 2 1

1 3 0 1 2

1 3 1 2 -1

2 3 3

1 2 0 2

1 2 1 2

1 2 1 -1

Output

5

7

正确解法：

第一个样例，一人从0站乘坐1号公交车途径1站，到2站下车，花费2S；此时2号车位于-1站，再经过2S，2号车从-1站途径1站到2站，人上2号车再经过1S到达-1站，共花费5S。或者一人从0站乘坐一号公交车到1站下车，花费1S，此时2号车位于2站，再经过2S到1站，人上2号车再经过2S到达-1站，共花费5S。

首先判断学校到火车东站能不能到站，即是否在同一个集团里面，用并查集就可以了。然后跑网络流，网络流跑一次后会更改原来储存的边的信息，因此可以枚举时间进行网络流，按照时间建边，在上一个时间段跑网络流的基础上，继续建图在继续跑网络流，将每次的最大流加起来直到总和大于等于k就可以返回当前天数了。

具体操作是将第i-1小时的第j个车的信息向第i小时的第j个车进行连边，容量为INF，将每辆车第i-1小时所待的公交车站向第i小时所待的公交车站连边，容量为车的最大载人数。

 

#include <bits/stdc++.h>
//CLOCKS_PER_SEC
#define se second
#define fi first
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define Pii pair<int,int>
#define Pli pair<ll,int>
#define ull unsigned long long
#define pb push_back
#define fio ios::sync_with_stdio(false);cin.tie(0)
const double Pi=3.14159265;
const int N=1e3+5;
const ull base=163;
const int INF=0x3f3f3f3f;
using namespace std;
int n,m,k,s,t;
int head[10100],to[100010],cur[10100],nx[100010];
int cap[100010];
int tot=0;
void add(int x,int y,int c){
    to[tot]=y;
    nx[tot]=head[x];
    cap[tot]=c;
    head[x]=tot++;
    
    to[tot]=x;
    nx[tot]=head[y];
    cap[tot]=0;
    head[y]=tot++;
}
void init(int n){
    tot=0;
    memset(head,-1,sizeof(head));
}
int d[N];
int bfs(){
    memset(d,-1,sizeof(d));
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];~i;i=nx[i]){
            int v=to[i];
            if(d[v]==-1&&cap[i]>0){
                d[v]=d[u]+1;
                q.push(v);
            }
        }
    }
    return d[t]!=-1;
}
int dfs(int s,int a){
    if(s==t||a==0)return a;
    int flow=0,f;
    for(int &i=cur[s];~i;i=nx[i]){
        int v=to[i];
        if(d[s]+1==d[v] && cap[i]>0 && (f=dfs(v,min(a,cap[i])))>0){
            flow+=f;
            cap[i]-=f;
            cap[i^1]+=f;
            a-=f;
            if(a==0)break;
        }
    }
    return flow;
}
int dinic(){
    int ans=0;
    while(bfs()){
        for(int i=0;i<=1000;i++)cur[i]=head[i];
        while(int di=dfs(s,INF)){
            ans+=di;
        }
    }
    return ans;
}
int ship[N][N];
int num[N];
int r[N];
int fa[N];
int F(int x){
    return fa[x]==x?x:fa[x]=F(fa[x]);
}
 
bool check(int x,int y){
    if(F(x)==F(y))return 1;
    else return 0;
}
int cal(int a,int d){
    return d*n+a;
}
void solve(){
    int flow=0;
    int i;
    init(n);// n -1     n-1   0
    add(s,cal(n-1,0),INF);
    add(cal(n,0),t,INF);
    for(i=1;flow<k;i++){
        add(s,cal(n-1,i),INF);add(cal(n,i),t,INF);
        for(int j=1;j<=n;j++){
            add(cal(j,i-1),cal(j,i),INF);
        }
        for(int j=1;j<=m;j++){
            int a=(i-1)%num[j]+1;
            int b=i%num[j]+1;
            add(cal(ship[j][a],i-1),cal(ship[j][b],i),r[j]);
        }
        flow+=dinic();
        
    }
   printf("%d
",i-1);
}
int main(){
     // clock_t start, end;
    int T;scanf("%d",&T);
    while(T--){
        s=0,t=1000;
        scanf("%d%d%d",&n,&m,&k);
        for(int i=0;i<=n+2;i++)fa[i]=i;
        for(int i=1;i<=m;i++){
            scanf("%d%d",&r[i],&num[i]);
            for(int j=1;j<=num[i];j++){
                scanf("%d",&ship[i][j]);
                if(ship[i][j]==0)ship[i][j]=n+1;
                if(ship[i][j]==-1)ship[i][j]=n+2;
                if(j>1){
                    fa[F(ship[i][j-1])]=F(ship[i][j]);
                }
            }
        }
        n+=2;
        if(check(n, n-1)){
            solve();
        }
        else{
            printf("0
");
        }
    }
    // end = clock();
    // cout << "time :"<<(double)(end - start) / CLOCKS_PER_SEC << endl;
    return 0;
}
/*
*/

 

K: 快乐树论

Description

曾经有一位伟大的皇帝，他拥有n座城池并用n-1条无向道路相连，每条道路均有一个确定的长度和两个端点，保证城池与城池之间互达。有一天，皇帝决定将其中一条路拆掉，并重新将这条道路以同样的长度搭在两座城池之间，皇帝可能将这条路拆了又重新建在原处。现在皇帝想问问你，在只拆掉一条道路并重新建造一条同样长的在两座城池之间后，任意两个城池之前的距离和最小为多少呢？

Input

第一行输入一个n代表皇帝有n座城池，接下来n-1行输入a,b,c代表城池a,b之间有一条长为c的道路。 (2 ≤ n ≤ 5000, 1 ≤ ai, bi ≤ n, ai ≠ bi, 1 ≤ wi ≤ 106)

Output

 输出一行任意两城池之间的最小距离和。

Examples

Input

输入样例1：

3

1 2 2

1 3 4

输入样例2：

6

1 2 1

2 3 1

3 4 1

4 5 1

5 6 1

输入样例3：

6

1 3 1

2 3 1

Output

12

29

85

正确解法：

具体证明参考：https://blog.csdn.net/zhoufenqin/article/details/9821617

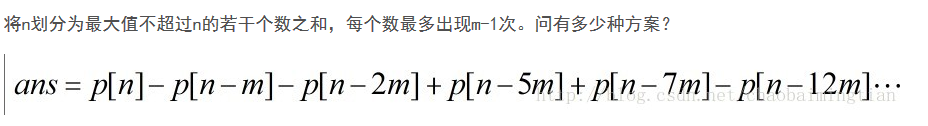
#include<bits/stdc++.h>
 
#define fi first
#define se second
#define pb push_back
 
using namespace std;
 
typedef long long ll;
typedef pair<ll,ll> Pll;
 
const ll LLMAX=2e18;
const int MAXN=1e6+10;
 
struct node{
    int u,v;
    ll w;
}in[MAXN];
 
ll dp[MAXN][3];
vector<Pll>G[MAXN];
 
void dfs(int u,int pre){
    dp[u][0]=dp[u][1]=dp[u][2]=0;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i].fi,w=G[u][i].se;
        if(v==pre)   continue;
        dfs(v,u);
        dp[u][2]+=dp[v][2]+dp[v][1]*dp[u][0]+dp[v][0]*dp[u][1]+dp[u][0]*dp[v][0]*w;
        dp[u][1]+=dp[v][1]+dp[v][0]*w;
        dp[u][0]+=dp[v][0];            
    }
    dp[u][0]++;
    dp[u][2]+=dp[u][1];
}
 
void solve(int u,int pre,ll &ans){
    ans=min(ans,dp[u][1]);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i].fi,w=G[u][i].se;
        if(v==pre)  continue;
        dp[v][1]=dp[v][1]+(dp[u][1]-dp[v][1]-w*dp[v][0])+(dp[u][0]-dp[v][0])*w;
        dp[v][0]=dp[u][0];
        solve(v,u,ans);
    }
}
 
int main(void)
{
    ios::sync_with_stdio(false);    cin.tie(0);
    ll n,ans=LLMAX;  cin>>n; 
    for(int i=1;i<n;i++){
        ll x,y,v;  cin>>x>>y>>v;    
        in[i].u=x,in[i].v=y,in[i].w=v;
        G[x].pb(Pll(y,v)),G[y].pb(Pll(x,v));
    }
    for(int i=1;i<n;i++){
        ll ans1=LLMAX,ans2=LLMAX,u=in[i].u,v=in[i].v,w=in[i].w;
        dfs(u,v);   solve(u,v,ans1);
        ll len1=(n-dp[u][0])*ans1+dp[u][2];
        dfs(v,u);   solve(v,u,ans2);
        ll len2=(n-dp[v][0])*ans2+dp[v][2];
        ans=min(ans,len1+len2+dp[u][0]*dp[v][0]*w);
    }
    cout<<ans<<endl;
    return 0;
}

L: 快乐数论

Description

给出正整数n,k，要求使正整数n拆分成若干个正整数的和，并且使得拆分后的数中相同的数的出现次数小于k次。

Input

第一行输入T,共有T组测试样例，接下来2~T+1行，每行输入n,k。 1<=n,k,T<=10^5

Output

输出T行，每行对应的拆分方案，最后答案取模1e9+7

Examples

Input

4

4 2

4 3

4 4

4 5

Output

2

4

4

5

正确解法：

n=4,k=2时，可拆分成4=4,4=1+3

n=4,k=3时，可拆分成4=1+2+1,4=2+2,4=1+3,4=4

 

#include<bits/stdc++.h>
 
using namespace std;
 
typedef long long  ll;
 
const int MOD=1e9+7;
const int MAXN=1e6+10;
 
ll p[MAXN];
 
void init(){
    p[0]=1;
    for(ll i=1;i<=100000;i++){
        for(ll j=1,w=1;w<=i;j++,w=(3*j*j+j)/2)
            if(j&1) p[i]=(p[i]+p[i-w])%MOD;
            else    p[i]=((p[i]-p[i-w])%MOD+MOD)%MOD;
        for(ll j=1,w=2;w<=i;j++,w=(3*j*j-j)/2)
            if(j&1) p[i]=(p[i]+p[i-w])%MOD;
            else    p[i]=((p[i]-p[i-w])%MOD+MOD)%MOD;
    }
}
 
ll solve(ll n,ll k){
    ll ans=p[n];
    for(ll j=1,w=k;w<=n;j++,w=k*(3*j*j+j)/2)
        if(j&1) ans=((ans-p[n-w])%MOD+MOD)%MOD;
        else    ans=(ans+p[n-w])%MOD;
    for(ll j=1,w=2*k;w<=n;j++,w=k*(3*j*j-j)/2)
        if(j&1) ans=((ans-p[n-w])%MOD+MOD)%MOD;
        else    ans=(ans+p[n-w])%MOD;
    return ans;
}
 
int main(void)
{
    init();
    int T;  cin>>T;
    while(T--){
        ll n,k;   scanf("%lld%lld",&n,&k);
        printf("%lld
",solve(n,k));
    }
    return 0;
}

 

 M: 看电影

Description

wjh要去看电影，邀请了lmb,xxb,cly,yzj,ckx等人，最后有k个人同意一起去。要去的电影院的位置是矩阵型的，其中’#’表示已经被人预定了，’*’表示空位，他们打算挑同一行或者同一列连续的座位坐在一起，现在给出k和位置的预定请况，试问有几种坐位置的方法。

Input

第一行输入两个数n和k，n表示电影院的位置是n*n的。（0<n<=10,0<=k<10）

接下在n行，每行n个字符，表示位置的预订情况。

Output

 一行输出有几种坐法。

Examples

Input

4 1

**##

*###

####

####

Output

4

正确解法：

暴力纵向横向搜索一下。

当k为0时，答案要除2。