思路:
没想到二维树状数组和一维的比只差了一行,update单点更新,query求和
这里的函数用法和平时不一样,query直接算出来就是某点的值,怎么做到的呢?
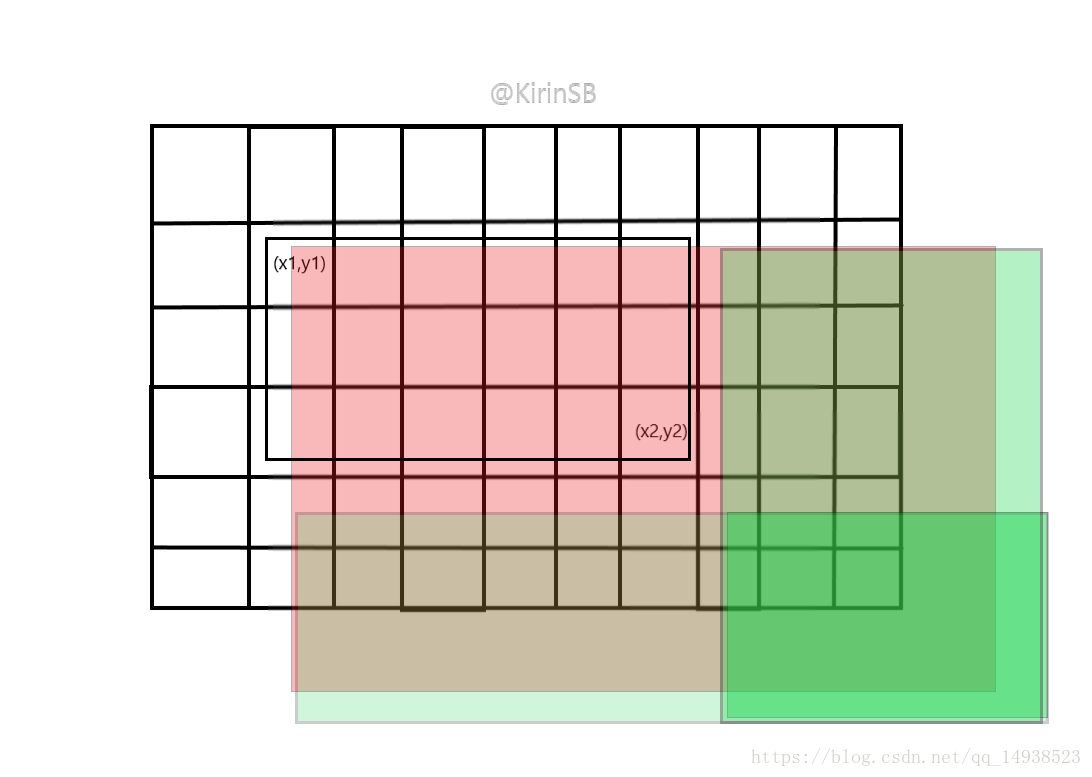
我们在更新的时候不止更新一个点,而是四个点,这样就会变成下图这样的效果
看不懂听我讲一下...这和上次嘉诚讲过的差分数组有点像(自觉回顾讲过什么),既然单点更新更新完是(1,1)~(x,y)的和在改变,那么我们只要在区间后面减去增加的,那么我们一算求和就等于求这个点的值了。我们要更新的实际上是黑框内区域,但是我们只更新(x1,y1)就只更新了红框区域,所以更新时多出来的三个点就是绿色的三块区域,因为是翻转问题,所以翻偶数次就是等于没翻,可以看到,最后绿色区域算上叠加都翻了偶数次,所以就抵消了。
代码:
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const int N = 1000+5;
int bit[N][N],n;
int lowbit(int x){
return x&(-x);
}
void update(int a,int b){
for(int i = a;i <= n;i += lowbit(i)){
for(int j = b;j <= n;j += lowbit((j))){
bit[i][j]++;
}
}
}
int query(int a,int b){
int ret = 0;
for(int i = a;i > 0;i -= lowbit(i)){
for(int j = b;j > 0;j -= lowbit(j)){
ret += bit[i][j];
}
}
return ret;
}
int main(){
int T,q,a,b,c,d;
char o[2];
scanf("%d",&T);
while(T--){
memset(bit,0,sizeof(bit));
scanf("%d%d",&n,&q);
for(int i = 0;i < q;i++){
scanf("%s",o);
if(o[0] == 'Q'){
scanf("%d%d",&a,&b);
printf("%d
",(query(a,b) - ) % 2);
}
else{
scanf("%d%d%d%d",&a,&b,&c,&d);
update(a,b);
update(c+1,b);
update(a,d+1);
update(c+1,d+1);
}
}
if(T) printf("
");
}
return 0;
}