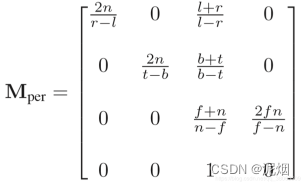该笔记基于闫令琪大神的cs课程及课后作业总结而成
目录
three-dimensional Euclidean space 三维欧氏空间
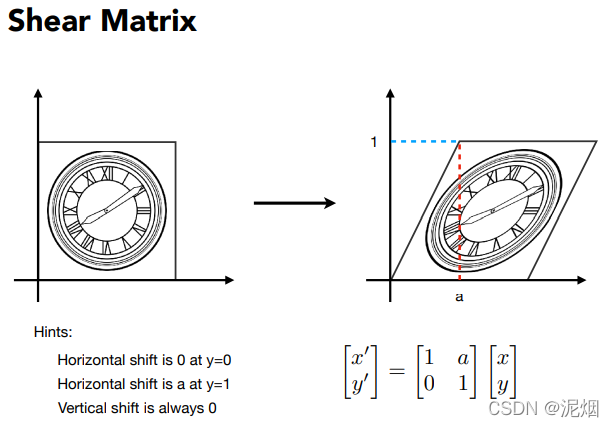

在伸缩,旋转后, 发现无法通过同维度的矩阵体现平移, 所以引入齐次方程

![]()
为了不把"平移变换"当做整个体系中的另类,再加一层向量,我的理解是补充常数(可以满足偏移等需求)

![]()


仿射变换


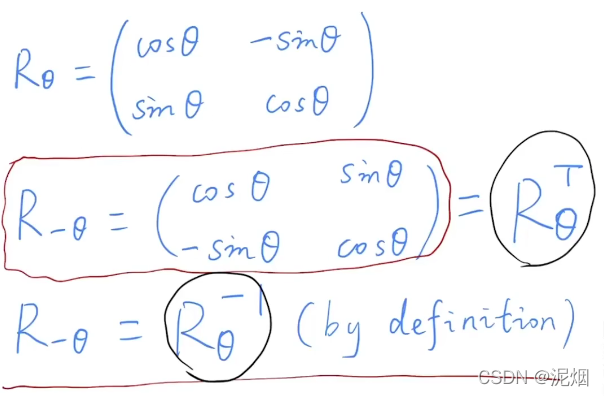

mvp变换
相机从一个坐标变换到世界坐标原点了,为了保持相机视图的图像不变,model也要跟着相机一起运动,相机变换到世界坐标的矩阵,就是model的变换矩阵,也就是MVP
先将当前物体的原点移至世界坐标原点T(view)
然后,为了求出当前整个参考系旋转至世界坐标系的变换R(view),可以先求其逆变换
旋转矩阵是正交矩阵 → 旋转矩阵的逆为它的转置,易得

正交投影
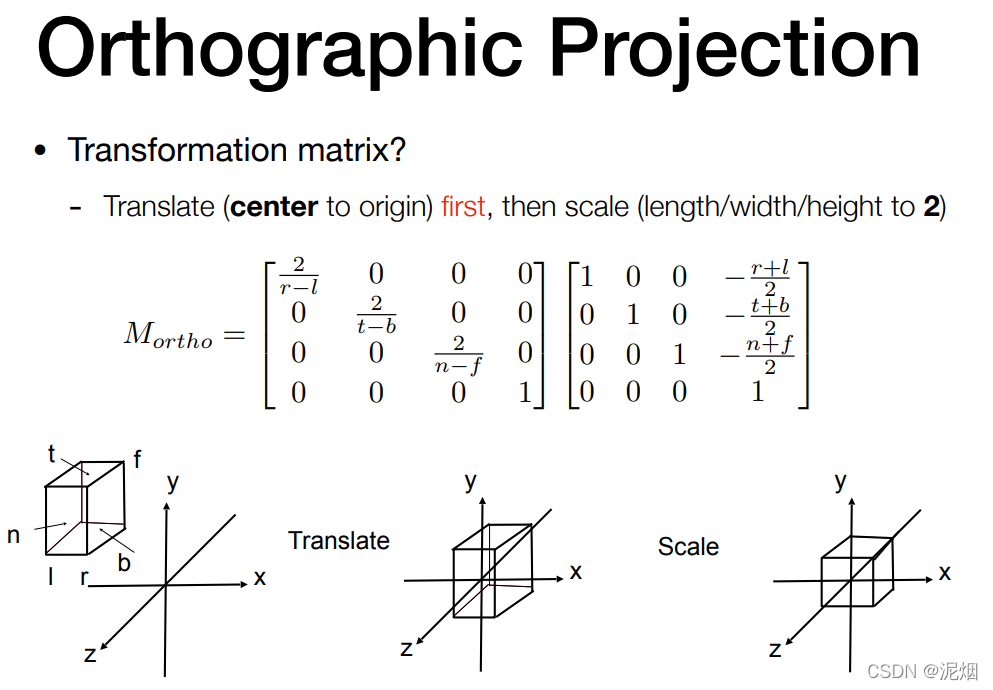
注意:
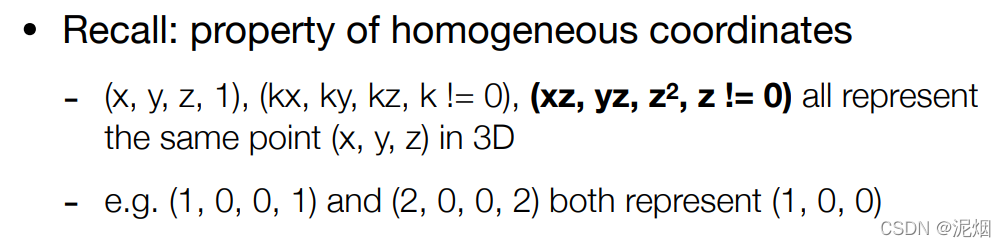
透射投影
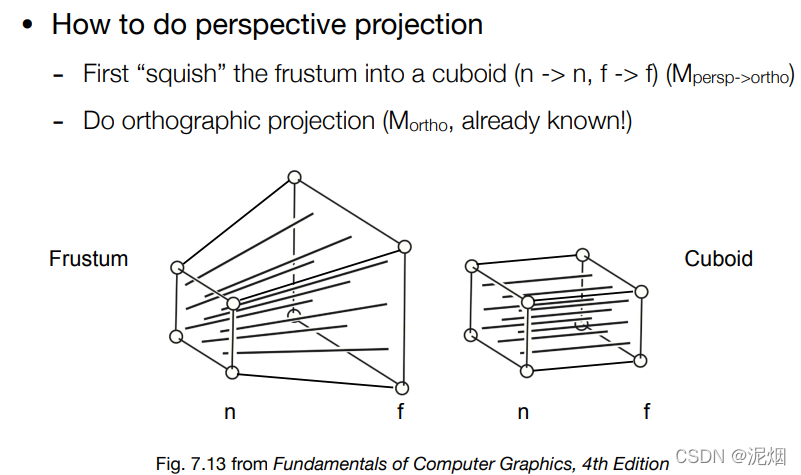
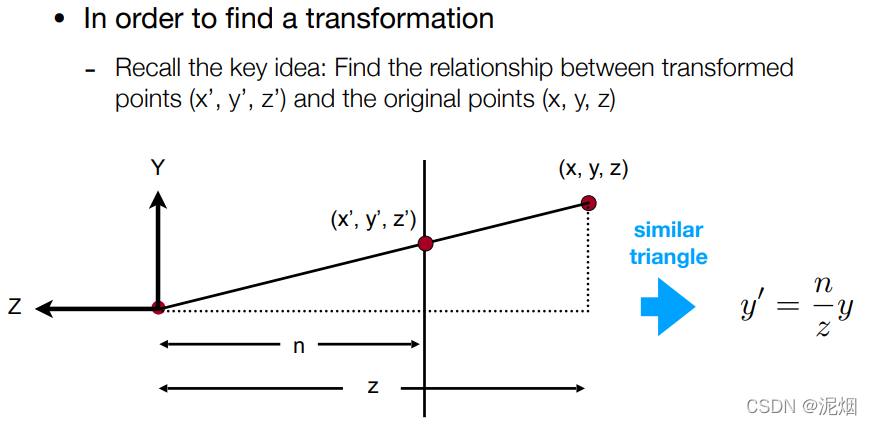

形象化的描述一下的话,就是利用这个变换矩阵将整个空间压缩了一下,使其对应了真正透视投影的坐标,最后不要忘了要利用正交转换到[-1, 1]^3的空间之内
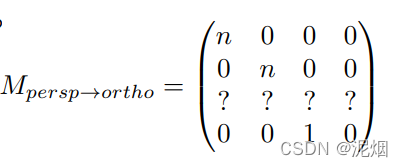


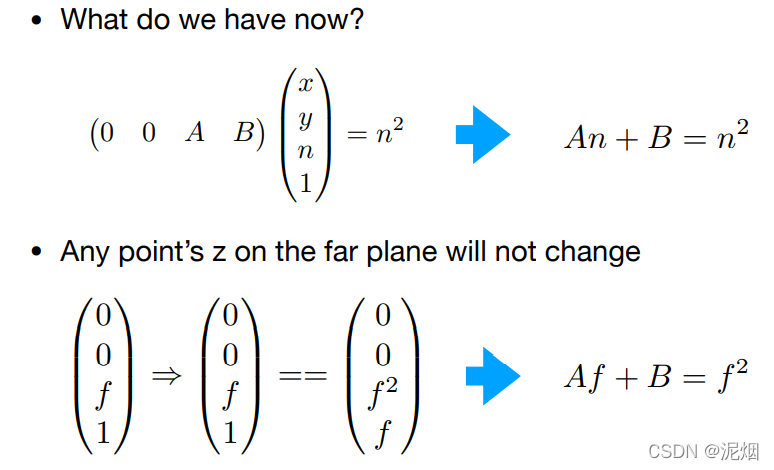
解得 A = n + f B = - f n
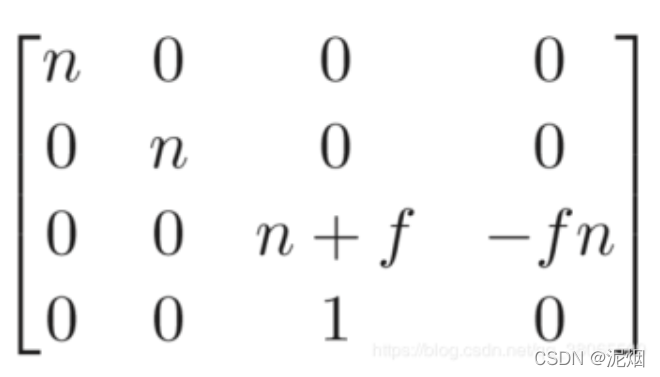
最后将这个被压缩过的空间,重新正交投影成标准小立方体,故定义透视投影变换
如下

即