[贪心/二分+kruskal] [JSOI2010]GROUP 部落划分 GROUP

[JSOI2010]GROUP 部落划分 GROUP (nowcoder.com)https://ac.nowcoder.com/acm/problem/20181

题目描述

聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。 不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了N个野人居住的地点（可以看作是平面上的坐标）。

我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了K个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。

他正在尝试这样一种算法： 对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。 

例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。

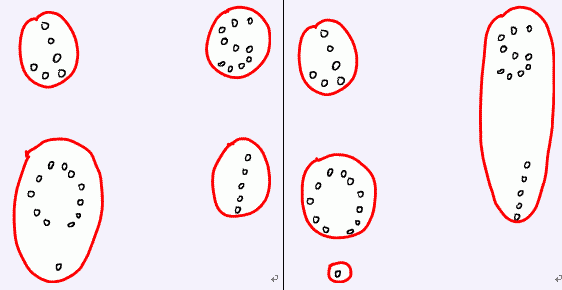
输入描述:

第一行包含两个整数N和K(1 ≤ N ≤ 1000,1 < K ≤ N)，分别代表了野人居住点的数量和部落的数量。
接下来N行，每行包含两个正整数x,y，描述了一个居住点的坐标(0 ≤ x, y ≤ 10000)

输出描述:

输出一行，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

示例1

输入

4 2
0 0
0 1
1 1
1 0

输出

1.00

备注:

对于100%的数据，保证 2≤k≤n≤10^3，0≤x,y≤10^4

由题意我们可以看出主体思路是求最小生成树, 当然,我们需要生成的其实是k棵树,并且保证生成的树中间距最小

题中有一句至关重要的话"使靠得最近的两个部落尽可能远离", 

这不由的使我联想到了二分(这题二分是可以做的,为保证精度, 左右区间之差要控制在0.0001之下), 

这里我用的是Kruskal算法(本质是贪心), 关键在于我们要生成的是k棵树,而总共有n个点, 那么在生成的过程中连接的次数为(n-k)时, 即有(n-k)条边时, 就已经生成了k棵树,那么当我们将要连第(n-k+1)条边时,此时对应的距离就是要求的最近距离中的最远(因为更小的已经在合并居住点的时候就已经"内耗掉了")

本题总结:

任意无自环无重边的图中满足,

b+k=n(b表示一个图中的边数,k表示连通分量,n表示点数)

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 1010;
struct edge{
    int a,b,w;
    bool operator<(const edge& p2)const{
        return w < p2.w;
    }
};

vector<edge> v;
int n,k;
int p[N],x[N],y[N];

int find(int x){
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
int main()
{
    cin >> n >> k;
    for(int i = 0; i < n; i ++)
    {
        p[i] = i;
        scanf("%d%d", &x[i], &y[i]);
    }
    
    for(int i = 0; i < n; i ++){
        for(int j = i+1; j < n; j ++){
            int d = (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
            v.push_back((edge){i, j, d});
        }
    }
    sort(v.begin(), v.end());
    
    int cnt = 0; //表示已经联通的边数
    int size = v.size();
    for(int i = 0; i < size; i ++)
    {
        int fa = find(v[i].a), fb = find(v[i].b);
        if(fa != fb)
        {
            p[fa] = fb;
            cnt ++;
            if(cnt == n-k+1){
                printf("%.2lf", sqrt(v[i].w));
                break;
            }
        }
    }
    return 0;
}