【BZOJ 3729】3729: Gty的游戏（Splay维护dfs序+博弈）

【分析】

　　膜奥爷爷啦~~

　　好吧，就是首先，阶梯尼姆，很明显吧。就是把距离根节点为奇数层的异或起来就好了。

　　那就是差不多维护子树的异或和，但是树是动态的。【表示动态树我真的很垃圾，splay忘光，LCT不会，前面做的题都是离线的【如果离线就很快就会做了

所以接下来要学学动态树了。。

　　用splay维护dfs序，和之前差不多嘛，一棵树的子树的dfs序记录了st和ed之后，查询区间[st,ed]就行了。

　　splay就是能求出键值在某范围里面的东西【具体维护什么，和啊，最大值啊，都是你决定的】，但实际splay树上维护的是splay树子树上的东西。

　　这时，你只要把st splay到跟，ed splay到根的右儿子，那么ed的做儿子表示的区间就是[st+1,ed-1]你直接问它的子树就好了。

　　实际上，并不需要实际的dfs序，只要你按顺序插入的，那splay树就是有序的，你记录每个点的st和ed，到时找前驱后继就好了。

　　可以选择看图：

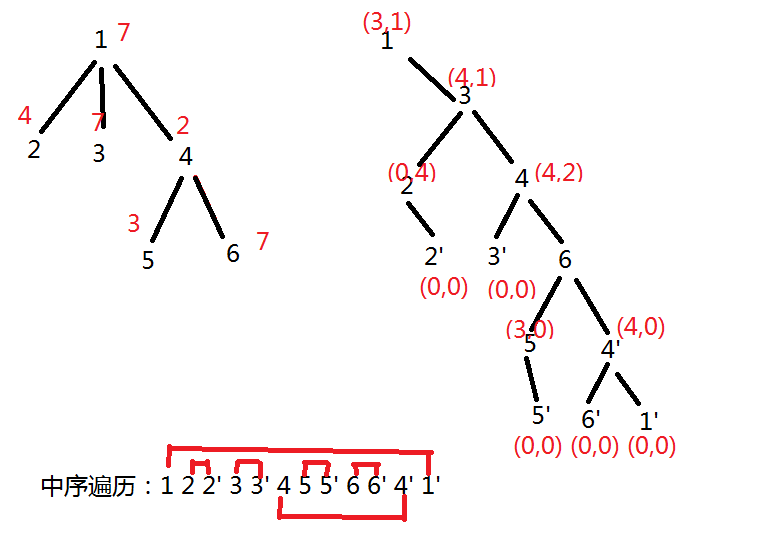
　　左图是原树，右图是splay树。红色是值。splay树的中序遍历就是dfs序，splay树上红色的两个维护的是子树内dep为奇和偶的点的异或和。

　　有意义的点我打在左端点，右端点的值均为0。

　　splay的时候upd一下把左右儿子的值跟自己异或一下就能维护那个异或和了。

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 #include<algorithm>
  6 #include<map>
  7 using namespace std;
  8 #define Maxn 400010
  9 
 10 int n,Mod;
 11 
 12 int w[Maxn];
 13 int nl[Maxn],nr[Maxn];
 14 map<int,int> z;
 15 
 16 struct node
 17 {
 18     int x,y,next;
 19 }t[Maxn*2];
 20 int len,first[Maxn];
 21 void ins(int x,int y)
 22 {
 23     t[++len].x=x;t[len].y=y;
 24     t[len].next=first[x];first[x]=len;
 25 }
 26 
 27 struct sp
 28 {
 29     int son[2],fa,d,a1,a2;
 30     bool dep;
 31 }tr[Maxn*2];int tot;
 32 
 33 void upd(int x)
 34 {
 35     int lc=tr[x].son[0],rc=tr[x].son[1];
 36     tr[x].a1=tr[lc].a1^tr[rc].a1;
 37     tr[x].a2=tr[lc].a2^tr[rc].a2;
 38     if(!tr[x].dep) tr[x].a2^=tr[x].d;
 39     else tr[x].a1^=tr[x].d;
 40 }
 41 void rot(int x)
 42 {
 43     int fa=tr[x].fa,yy=tr[fa].fa;
 44     int w=tr[fa].son[0]==x?1:0;
 45     tr[fa].son[1-w]=tr[x].son[w];
 46     if(tr[x].son[w]) tr[tr[x].son[w]].fa=fa;
 47     if(yy)
 48     {
 49         if(tr[yy].son[0]==fa) tr[yy].son[0]=x;
 50         else tr[yy].son[1]=x;
 51     }tr[x].fa=yy;
 52     tr[x].son[w]=fa;tr[fa].fa=x;
 53     upd(fa);upd(x);
 54 }
 55 void splay(int x,int nf)
 56 {
 57     while(tr[x].fa!=nf)
 58     {
 59         int fa=tr[x].fa,yy=tr[fa].fa;
 60         if(yy==nf) rot(x);
 61         else
 62         {
 63             if((tr[yy].son[0]==fa)==(tr[fa].son[0]==x)) {rot(fa);rot(x);}
 64             else {rot(x);rot(x);}
 65         }
 66     }
 67 }
 68 int Lower(int x)
 69 {
 70     splay(x,0);
 71     x=tr[x].son[1];
 72     while(tr[x].son[0]) x=tr[x].son[0];
 73     return x;
 74 }
 75 void insert(int fa,int x)
 76 {
 77     int r=Lower(fa);
 78     splay(fa,0);splay(r,fa);
 79     tr[r].son[0]=x;
 80     tr[x].fa=r;
 81     upd(r);upd(fa);
 82 }
 83 void dfs(int x,int fa)
 84 {
 85     tr[x].dep=!tr[fa].dep;
 86     if(fa)
 87     {
 88         tr[nl[x]].son[1]=nr[x];tr[nr[x]].fa=nl[x];
 89         tr[nl[x]].d=w[x];upd(nr[x]);upd(nl[x]);
 90         insert(fa,x);
 91     }
 92     for(int i=first[x];i;i=t[i].next) if(t[i].y!=fa)
 93     {
 94         int y=t[i].y;
 95         dfs(y,x);
 96     }
 97 }
 98 
 99 int main()
100 {
101     scanf("%d%d",&n,&Mod);Mod++;
102     for(int i=1;i<=n;i++) {scanf("%d",&w[i]);z[i]=i;w[i]%=Mod;}
103     for(int i=1;i<n;i++)
104     {
105         int x,y;
106         scanf("%d%d",&x,&y);
107         ins(x,y);ins(y,x);
108     }
109     for(int i=1;i<=n;i++) nl[i]=i,nr[i]=i+n;tot=n*2;
110     tr[0].dep=0;tr[1].son[1]=n+1;
111     tr[1].d=w[1];tr[n+1].fa=1;upd(n+1);upd(1);
112     dfs(1,0);
113     int q,nw=0;
114     scanf("%d",&q);
115     while(q--)
116     {
117         int opt,ans;
118         int x,y,k;
119         scanf("%d",&opt);
120         if(opt==1)
121         {
122             scanf("%d",&x);
123             x^=nw;
124             x=z[x];
125             splay(nl[x],0);splay(nr[x],nl[x]);
126             if(!tr[x].dep) ans=tr[tr[nr[x]].son[0]].a1;
127             else ans=tr[tr[nr[x]].son[0]].a2;
128             if(ans==0) printf("GTY
");
129             else {printf("MeiZ
");nw++;}
130         }
131         else if(opt==2)
132         {
133             scanf("%d%d",&x,&y);
134             x^=nw;y^=nw;
135             y%=Mod;
136             x=z[x];
137             splay(nl[x],0);
138             if(!tr[nl[x]].dep) tr[nl[x]].a2^=y^tr[nl[x]].d;
139             else tr[nl[x]].a1^=y^tr[nl[x]].d;
140             tr[nl[x]].d=y;
141         }
142         else
143         {
144             scanf("%d%d%d",&x,&y,&k);
145             x^=nw;y^=nw;k^=nw;
146             k%=Mod;x=z[x];z[y]=y=++n;
147             nl[y]=++tot;nr[y]=++tot;
148             tr[nl[y]].dep=!tr[nl[x]].dep;
149             tr[nl[y]].d=k;tr[nr[y]].d=0;
150             tr[nr[y]].fa=nl[y];
151             tr[nl[y]].fa=nl[x];upd(nl[y]);upd(nr[y]);
152             insert(nl[x],nl[y]);
153         }
154     }
155     return 0;
156 }

View Code

【AC了还是很兴奋的。。。以后要多做点dfs序，splay之类的。。

2017-03-30 16:39:42

【BZOJ 3729】3729: Gty的游戏（Splay维护dfs序+博弈）

未经博主同意不得转载

3729: Gty的游戏

Description

Input

Output

Sample Input

Sample Output

HINT

Source

【BZOJ 3729】3729: Gty的游戏 （Splay维护dfs序+博弈）

未经博主同意不得转载

3729: Gty的游戏

Description

Input

Output

Sample Input

Sample Output

HINT

Source

【BZOJ 3729】3729: Gty的游戏（Splay维护dfs序+博弈）