二叉树基本算法

仅供JavaScript刷题参考用。

二叉查找树和平衡二叉树

其它树：满二叉树、完全二叉树、完美二叉树、哈弗曼树、二叉查找树BST、平衡二叉树AVL
了解：红黑树，是一种特殊的二叉树。这种树可以进行高效的中序遍历

建立

创建BinarySearchTree类。首先，声明它的结构：

（注意，BinarySearchTree是个类，后面所有函数都定义在该结构体内）

function BinarySearchTree() {
    //私有的辅助函数
    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };
    //声明一个私有变量以控制此数据结构的第一个节点。在树中，它不是头节点，而是根元素
    var root = null;
}

插入

this.insert = function(key){
    var newNode = new Node(key);
    if (root === null){
        root = newNode;
    } else {
        insertNode(root,newNode);
    }
};

// 私有的辅助函数
var insertNode = function (node, newNode) {
    if (newNode.key < node.key) {
        if (node.left === null) {
            node.left = newNode;
        } else {
            insertNode(node.left, newNode);
        }
    } else {
        if (node.right === null) {
            node.right = newNode;
        } else {
            insertNode(node.right, newNode);
        }
    }
};

删除

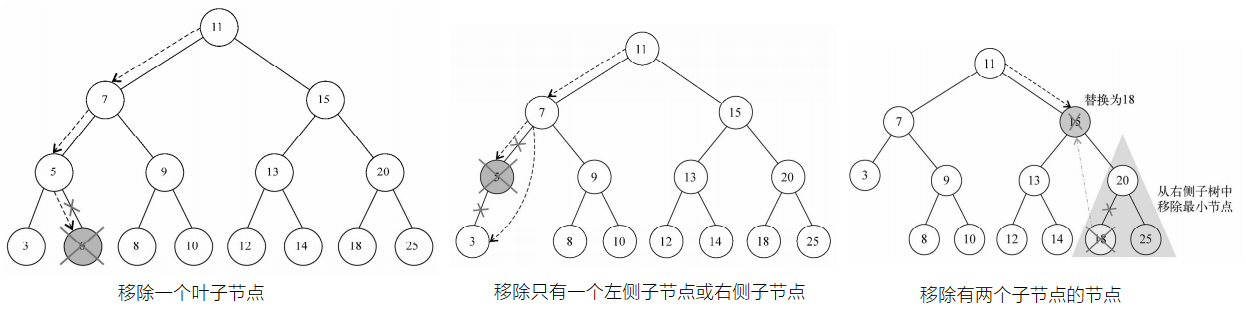
this.remove = function (key) {
    root = removeNode(root, key);
};

var removeNode = function (node, key) {
    if (node === null) {
        return null;
    }
    if (key < node.key) {
        node.left = removeNode(node.left, key);
        return node;
    } else if (key > node.key) {
        node.right = removeNode(node.right, key);
        return node;
    } else { //键等于node.key
        //第一种情况——一个叶节点
        if (node.left === null && node.right === null) {
            node = null;
            return node;
        }
        //第二种情况——一个只有一个子节点的节点
        if (node.left === null) {
            node = node.right;
            return node;
        } else if (node.right === null) {
            node = node.left;
            return node;
        }
        //第三种情况——一个有两个子节点的节点
        var aux = findMinNode(node.right);
        node.key = aux.key;
        node.right = removeNode(node.right, aux.key);
        return node;
    }
};

查找

this.search = function (key) {
    return searchNode(root, key);
};

var searchNode = function (node, key) {
    if (node === null) {
        return false;
    }
    if (key < node.key) {
        return searchNode(node.left, key);
    } else if (key > node.key) {
        return searchNode(node.right, key);
    } else {
        return true;
    }
};

寻找最大值

this.max = function () {
    return maxNode(root);
};

var maxNode = function (node) {
    if (node) {
        while (node && node.right !== null) {
            node = node.right;
        }
        return node.key;
    }
    return null;
};

寻找最小值

this.min = function () {
    return minNode(root);
};

var minNode = function (node) {
    if (node) {
        while (node && node.left !== null) {
            node = node.left;
        }
        return node.key;
    }
    return null;
};

遍历

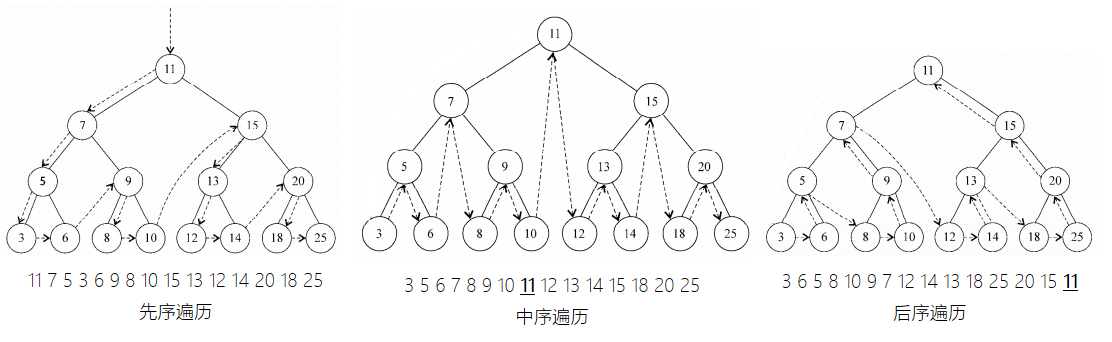
✔先序

this.preOrderTraverse = function (callback) {
    preOrderTraverseNode(root, callback);
};

var preOrderTraverseNode = function (node, callback) {
    if (node !== null) {
        callback(node.key);
        preOrderTraverseNode(node.left, callback);
        preOrderTraverseNode(node.right, callback);
    }
};

✔中序

this.inOrderTraverse = function (callback) {
    inOrderTraverseNode(root, callback);
};

var inOrderTraverseNode = function (node, callback) {
    if (node !== null) {
        inOrderTraverseNode(node.left, callback);
        callback(node.key);
        inOrderTraverseNode(node.right, callback);
    }
};

✔后序

this.postOrderTraverse = function (callback) {
    postOrderTraverseNode(root, callback);
};

var postOrderTraverseNode = function (node, callback) {
    if (node !== null) {
        postOrderTraverseNode(node.left, callback);
        postOrderTraverseNode(node.right, callback);
        callback(node.key);
    }
};

✔深度优先（DFS)

在二叉树中，DFS就相当于先序遍历

✔广度优先（BFS）/层次遍历

利用队列来模拟，就很容易了

this.bfsTraverse = function (callback) {
    bfsTraverseNode(root, callback)
}

var bfsTraverseNode = function (root, callback) {
    var queue = []
    if(root){
        queue.push(root)
    }
    while(queue.length){
        var node = queue.shift()
        callback(node.key)
        if(node.left){
            queue.push(node.left)
        }
        if(node.right){
            queue.push(node.right)
        }
    }
}

线索化二叉树