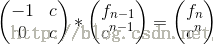矩阵快速幂

所谓矩阵快速幂就是把快速幂中的乘运算替换为矩阵乘。

解决 fab时 f(n)=f(n-1)+f(n-2) 则可得到    1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

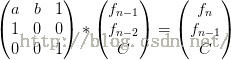
2.f(n)=c^n-f(n-1) ；（c是常数）

  

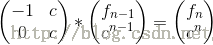
 一般这种题目都是要找递推式，这是难点.

struct Mat
{
    LL m[101][101];
};//存储结构体
Mat a,e; //a是输入的矩阵，e是输出的矩阵
Mat Mul(Mat x,Mat y)
{
    Mat c;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            c.m[i][j] = 0;
        }
    }
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            for(int k=1;k<=n;++k){
                c.m[i][j] = c.m[i][j]%mod + x.m[i][k]*y.m[k][j]%mod;
            }
        }
    }
    return c;
}
Mat pow(Mat x,LL y)//矩阵快速幂
{
    Mat ans = e;
    while(y){
        if(y&1) ans = Mul(ans,x);
        x = Mul(x,x);
        y>>=1;
    }
    return ans;
}