题目大意
出于某种原因,农夫约翰的牛总是在举行激光表演。
对于他们的最新展会,奶牛已经购买了一个大功率的激光器 - 这么大,事实上,他们似乎不能轻易地从它交付的位置移动。他们想以某种方式将激光的光发送到FJ物业另一侧的谷仓。激光器和谷仓都可以被认为位于FJ农场的地图上的2D平面中的点上。牛计划指挥激光器,使得它发出水平或竖直(即,与x或y轴平行)的光束。他们会将这个光束从一些镜子反射回去,直接到谷仓。
在农场上有N个栅栏(1≤N≤100,000),位于不同的二维点(也不同于激光和谷仓),牛可以安装镜子。可以选择不在护栏柱上安装镜子,在这种情况下,激光器将简单地直接通过柱子的顶部而不改变方向。如果母牛确实在栅栏柱上安装了一个镜子,它们会像/或对齐,使得它将在垂直方向上重定向光束,反之亦然。
请计算牛需要使用的镜子的最小可能数量,以便将激光重新导向谷仓。
题目分析
考虑装了镜子后会有什么效果。
若一束光打过来到一个护栏上,沿原方向出去花费为0,改变90°后出去花费为1。
所以考虑把一个点拆成四个点。(这里借用洛谷大佬 _Yunluo_的一张图)(点开后为他滴题解)
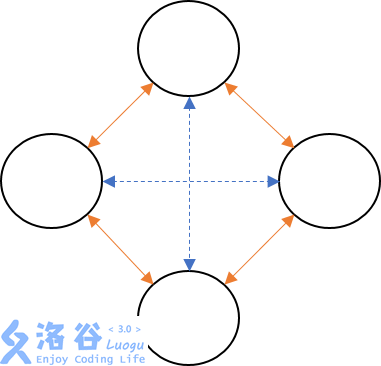
这样,蓝色边权为0,橙色边权为1。
至此,我们完成了“装镜子”,这个操作。
然后我们把所有点分别按照横坐标,纵坐标排序,建边。跑一遍最短路就行。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int MAXN=1e5+10; 4 const int Inf=0x3f3f3f3f; 5 struct Node{ 6 int x,y,id; 7 }p[MAXN+10]; 8 struct Egde{ 9 int to,nxt,d; 10 }e[MAXN<<4]; 11 int cnt,head[MAXN<<3]; 12 inline void add_edge(int u,int v,int d){ 13 e[++cnt].to=v;e[cnt].d=d;e[cnt].nxt=head[u];head[u]=cnt; 14 } 15 inline bool cmp1(Node a,Node b){ 16 return a.x==b.x?a.y<b.y:a.x<b.x; 17 } 18 inline bool cmp2(Node a,Node b){ 19 return a.y==b.y?a.x<b.x:a.y<b.y; 20 } 21 22 int n,S,T,p_cnt; 23 int new_Node[MAXN][4]; 24 int dis[MAXN*4+10]; 25 bool vis[MAXN*4+10]; 26 queue<int> q; 27 inline void SPFA(){ 28 for(int i=1;i<=MAXN*4;++i) 29 dis[i]=Inf; 30 q.push(S); 31 vis[S]=1; 32 dis[S]=0; 33 while(!q.empty()){ 34 int x=q.front(); 35 q.pop(); 36 vis[x]=false; 37 for(int i=head[x],y;i;i=e[i].nxt){ 38 y=e[i].to; 39 if(dis[y]>dis[x]+e[i].d){ 40 dis[y]=dis[x]+e[i].d; 41 if(!vis[y]){ 42 q.push(y); 43 vis[y]=true; 44 } 45 } 46 } 47 } 48 } 49 50 int main(){ 51 for(int i=1;i<=MAXN;++i) p[i].id=i; 52 scanf("%d%d%d%d%d",&n,&p[1].x,&p[1].y,&p[2].x,&p[2].y); 53 n+=2; 54 for(int i=3;i<=n;++i) 55 scanf("%d%d",&p[i].x,&p[i].y); 56 S=++p_cnt;T=++p_cnt; 57 for(int i=1;i<=n;++i) 58 for(int j=0;j<=3;++j) 59 new_Node[i][j]=++p_cnt; 60 for(int i=1;i<=n;++i){ 61 add_edge(new_Node[i][0],new_Node[i][1],0);add_edge(new_Node[i][1],new_Node[i][0],0); 62 add_edge(new_Node[i][2],new_Node[i][3],0);add_edge(new_Node[i][3],new_Node[i][2],0); 63 64 add_edge(new_Node[i][2],new_Node[i][0],1);add_edge(new_Node[i][0],new_Node[i][2],1); 65 add_edge(new_Node[i][2],new_Node[i][1],1);add_edge(new_Node[i][1],new_Node[i][2],1); 66 67 add_edge(new_Node[i][3],new_Node[i][0],1);add_edge(new_Node[i][0],new_Node[i][3],1); 68 add_edge(new_Node[i][3],new_Node[i][1],1);add_edge(new_Node[i][1],new_Node[i][3],1); 69 } 70 sort(p+1,p+n+1,cmp1); 71 for(int i=2;i<=n;++i) 72 if(p[i].x==p[i-1].x){ 73 add_edge(new_Node[p[i-1].id][3],new_Node[p[i].id][2],0); 74 add_edge(new_Node[p[i].id][2],new_Node[p[i-1].id][3],0); 75 } 76 sort(p+1,p+n+1,cmp2); 77 for(int i=2;i<=n;++i) 78 if(p[i].y==p[i-1].y){ 79 add_edge(new_Node[p[i-1].id][1],new_Node[p[i].id][0],0); 80 add_edge(new_Node[p[i].id][0],new_Node[p[i-1].id][1],0); 81 } 82 for(int i=0;i<=3;++i){ 83 add_edge(S,new_Node[1][i],0); 84 add_edge(new_Node[2][i],T,0); 85 } 86 //cout<<1<<endl; 87 SPFA(); 88 printf("%d ",dis[T]>=Inf?-1:dis[T]); 89 return 0; 90 }