「2019冬令营提高组」直径

传送门

考虑一颗 $n$ 个叶节点的菊花树的情况，边权均为1

显然直径数为 $n*(n-1)/2$(20分)

考虑两颗菊花树的情况:

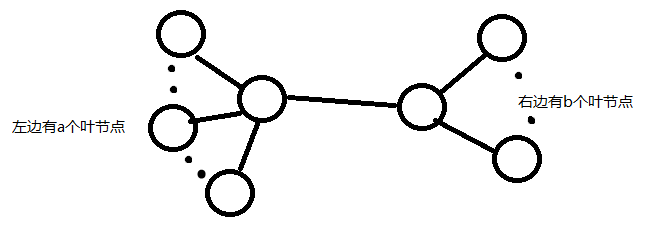
那么直径有 $a*b$ 个，但是对于 $n$ 为大质数的情况还是不够(40分)

那么考虑三个菊花树的情况:

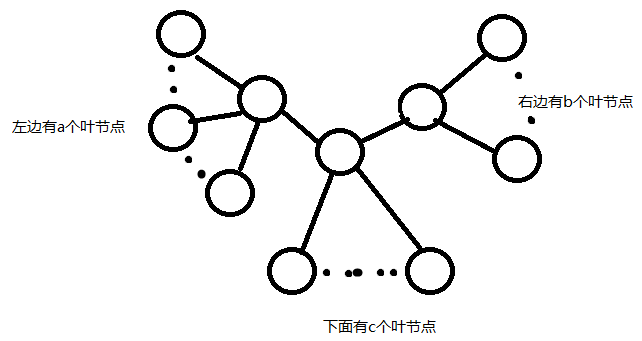
答案也十分显然，为 $a*(b+c)+b*c$

所以枚举 $a$ 和 $b$ 然后计算 $c$，判断是否符合条件

此时已经有很大概率存在 $a,b,c$ 符合条件了，写出代码后枚举 $n$ 发现都有解

所以就只要三颗菊花树(100分)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
int n;
int main()
{
    freopen("diameter.in","r",stdin);
    freopen("diameter.out","w",stdout);
    n=read();
    int t=sqrt(n*8+1);
    if(t*t==n)//一颗菊花树的情况
    {
        int cnt=0,i=1;
        while(i)
        {
            cnt+=i; if(cnt==n) break;
            i++;
        }
        printf("%d
",i+1);
        for(int j=1;j<=i;j++) printf("%d %d %d
",1,j+1,1);
        return 0;
    }
    for(int k1=1;k1<=2499;k1++)//枚举第一颗菊花树
        for(int k2=k1;k2<=5000-k1-3;k2++)//枚举第二课菊花树
        {
            int t=n-k1*k2;//求出第三颗菊花树
            if(!t)
            {
                printf("%d
",k1+k2+3);
                printf("%d %d %d
",1,2,1); printf("%d %d %d
",1,3,1);
                for(int i=1;i<=k1;i++) printf("%d %d %d
",2,3+i,1);
                for(int i=1;i<=k2;i++) printf("%d %d %d
",3,3+k1+i,1);
                return 0;
            }
            if(t<0||t%(k1+k2)!=0) continue;
            int k3=t/(k1+k2);
            if(k1+k2+k3+4<=5000)
            {
                printf("%d
",k1+k2+k3+4);
                printf("%d %d %d
%d %d %d
%d %d %d
",1,2,1,1,3,1,1,4,1);
                for(int j=1;j<=k1;j++) printf("%d %d %d
",2,4+j,1);
                for(int j=1;j<=k2;j++) printf("%d %d %d
",3,4+k1+j,1);
                for(int j=1;j<=k3;j++) printf("%d %d %d
",4,4+k1+k2+j,1);
                return 0;
            }
        }
    return 0;
}