主席树解法
设las[ i ]表示数列中第 i 个数的值 上一次出现的位置,num[ i ]为原数列中第 i 个数的值
1. 把 从第 1 到第 i 个数的 las 的值 的出现次数 建立一个线段树
那么第 i 个叶子节点 i 就表示 las 值为 i-1 的出现次数
对于序列 1 2 1 3 4 1 建立的线段树如图:
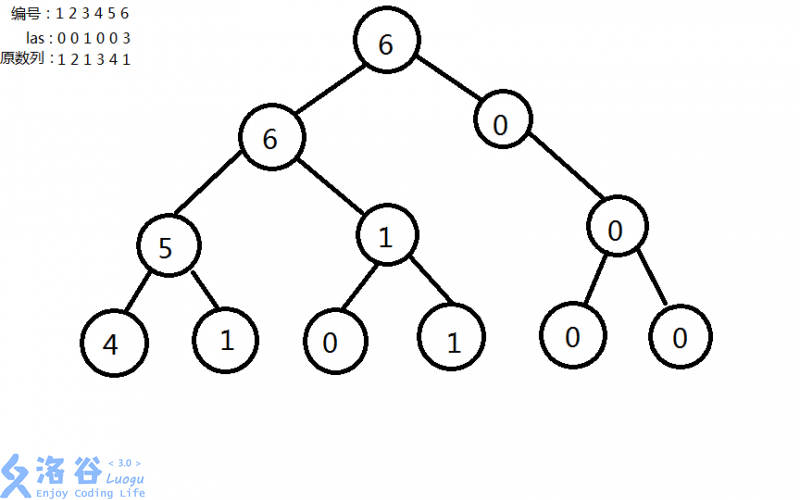
2. 一共有 n 个线段树,合在一起就是主席树(要对每个 i 建立线段树)
3. 询问 l,r 就只要把第 r 个线段树中从 0 到 l-1 的值的和 减去第 l-1 个个线段树从 0 到 l-1 的值的和。
关于第3点的证明:
想一想,对于同一个 i , 第 r 个线段树的叶子节点 i 减去第 l-1 个线段树的叶子节点 i 的值( i 从 0 到 l-1) 就表示从 l~r 区间多出了的 区间 l~r (注意是从 l 到 r ) 中第一次出现的数字 a (a 为 num[ i ])的数量(多出的数量为 1 或 0,除非 i 等于 0)
因为如果区间 l~r 中第 j 个数 a 再次出现(再次出现意思是数列 l~r 中已经有出现过 a 了),那么las[ j ]就为 区间l~r 中 的前面同一个数 a 的位置(显然 l<= las[ j ] <= r),不会更新叶子节点i的值(因为 0<= i <= l-1),因此可以把叶子节点的值拿来相减,既然叶子可以相减,那么它们的父节点也能相减.
思路懂了就不难了..
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> using namespace std; const int N=500007; int n,m,cnt; int las[N],pre[N]; //------以下为主席树------ int rt[N],L[N<<8],R[N<<8],sum[N<<8]; inline int build(int pre,int l,int r,int v) { int root=++cnt; sum[root]=sum[pre]+1; if(l==r) return root; L[root]=L[pre]; R[root]=R[pre]; int mid=(l+r)>>1; if(v<=mid) L[root]=build(L[pre],l,mid,v); else R[root]=build(R[pre],mid+1,r,v); return root; } inline int query(int hea,int las,int l,int r,int ql) { if(r<=ql) return sum[las]-sum[hea]; int mid=(l+r)>>1; int res=query(L[hea],L[las],l,mid,ql); return mid>=ql ? res : res+query(R[hea],R[las],mid+1,r,ql); } //------以上为主席树------ int main() { int a; cin>>n; for(int i=1;i<=n;i++) { scanf("%d",&a); las[i]=pre[a]; pre[a]=i; } for(int i=1;i<=n;i++) rt[i]=build(rt[i-1],0,n,las[i]);//注意l从0开始 cin>>m; int l,r; while(m--) { scanf("%d%d",&l,&r); printf("%d ",query(rt[l-1],rt[r],0,n,l-1));//注意l从0开始 } return 0; }