哈希
首先要知道一个结论:
判断一个串s中 长度为k的串是不是循环节 的充分必要条件是:
s[1]~s[len-k] = s[k] ~ s[len] 并且 len%k=0
怎么证明呢
如图:
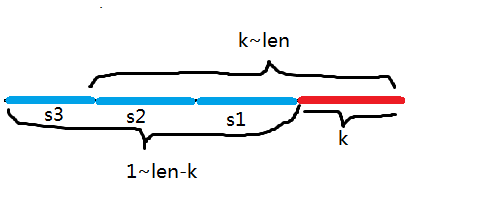
显然红色的串=s1(因为s[1]~s[len-k] = s[k] ~ s[len])
同样s1=s2,s2=s3
显然只要有重复串就一定会形成类似的这种情况
所以我们就可以利用这点来O(1)判断该串是否为循环节
但是如果枚举长度k
时间无法承受
考虑如何优化
可以发现 len 一定是 k 的倍数
可以利用这一点来搞优化
把 len 从小到大枚举质因数
那么显然 k 一定是其中几个质因数的乘积
要如何找出最小的 k 呢
我们可以把 len 分别除以它的所有质因数
如果长度为 len/prime_a 的串是循环节
那么就把 len除以prime_a 然后继续枚举其他质因数
尝试能否再次减小len
最后的 len 就是我们要找的 k
怎么从大到小枚举 len 的质因数也容易
用欧拉筛的时候我们可以得到每个数的最小质因数(记为nex[ i ])
只要不断把 nex [ len ] 记录下来然后 len /= nex [ len ] 就行了
总复杂度约为O(q log n)
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; typedef unsigned long long ull; const int N=1000007; const int base=23333; int n,m,a[N],l,r; int t[N],tot,nex[N]; ull h[N],fac[N]; char s[N]; int pri[N],cnt; bool not_pri[N]; inline void prenex()//欧拉筛预处理nex { not_pri[1]=1; nex[1]=1; for(int i=2;i<=n;i++) { if(!not_pri[i]) pri[++cnt]=i,nex[i]=i; for(int j=1;j<=cnt;j++) { long long g=(long long)i*pri[j]; if(g>n) break; not_pri[g]=1; nex[g]=pri[j]; if(i%pri[j]==0) break; } } } inline bool pd(int la,int ra,int lb,int rb) //判断串s[la]~s[ra]是否等于s[lb]~s[rb] { ull h1=h[ra]-h[la-1]*fac[ra-la+1]; ull h2=h[rb]-h[lb-1]*fac[rb-lb+1]; return h1==h2; } int main() { cin>>n; prenex(); scanf("%s",s+1); fac[0]=1; for(int i=1;i<=n;i++) { a[i]=s[i]-'0'; h[i]=h[i-1]*base+a[i]; fac[i]=fac[i-1]*base; }//预处理哈希值 cin>>m; while(m--) { scanf("%d%d",&l,&r); int len=r-l+1,tot=0; while(len!=1) { t[++tot]=nex[len]; len/=nex[len]; }//从小到大找出len的质因数 len=r-l+1; for(int i=1;i<=tot;i++) { int g=len/t[i]; if(pd(l,r-g,l+g,r)) len=g; }//尝试减小len printf("%d ",len); } return 0; }