来自各个大佬的讲解与证明：
二次剩余Cipolla算法学习笔记 - bztMinamoto - 博客园
[数论]二次剩余及计算方法 – Miskcoo's Space
浅谈二次剩余 - stevensonson的博客 - CSDN博客
二次剩余入门 - Eiffel的博客 - CSDN博客
图文]第4章二次同余方程 - 百度文库
二次剩余Cipolla算法学习小记 - 待成熟的葡萄 - CSDN博客
发现自己再回来看，忘了是怎么弄了，还是写一下自己的体会，方便理解。
首先二次剩余是什么？也就是a∈Z,gcd(a,m)=1,如果x2Ξa(mod m)有解，那么a就是模m的二次剩余
当m小的时候，我们直接把0,1,2,..m/2代入计算就可以判断有没有解，而当m很大的时候，如果m是合数的时候比较难解决，所以我们就只来讨论m是奇素数p的时候。
有个结论，欧拉判别条件：
a是模p的二次剩余的充要条件是a(p-1)/2Ξ1(mod p)
a是模p的非二次剩余的充要条件是a(p-1)/2Ξ-1(mod p)
且a是p的二次剩余的时候，同余方程恰好有两个解
证明是不会的，这辈子都不可能去证明了的。想看详细证明的可以翻一翻上面的博客。
然后平方剩余的一些性质
若a1,a2都是模p的二次剩余，a1*a2也是模p的二次剩余
若a1,a2都是模p的非二次剩余，a1*a2是模p的二次剩余
若a1是模p的二次剩余,a2是模p的非二次剩余,a1*a2是模p的非二次剩余
接下来有一个概念：勒让得符号(legender symbol)
根据上面的定义就有：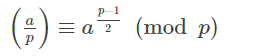
所以这3个描述是等价的
概念了解得差不多了，那怎么就是怎么求x2Ξa(mod m)的解x
就很霸道的一句话
设b满足b2-a是模p的非二次剩余，设ω=√b2-a,那么x≡(b+ω）(p+1)/2是x2Ξa(mod m)的解
理解是话，按照设定w是模p不能开根号的，那我们非要给w开根号，那么它所在的值域就变了，我们假设一个域为Fp2,那这其实是一个类似复数域的存在，
所以这里理解的话ω，可以视为复数的那个虚部的i，Fp2域的数就可以表示为x+yω，且这个域是满足其他域的性质，也可以四则运算。那么，x≡(b+ω）(p+1)/2也就是一个合法的数
然后为什么这就是同余方程的解呢。
用以下几个定理来解释
定理1.ωpΞ-ω (mod p)
证明：ωp=ω*ωp-1=ω*(ω2)(p-1)/2=ω*(b2-a)(p-1)/2=ω*-1 (mod p)
定理2.(a+b)n=an+bn (mod p)
证明：二项式展开就有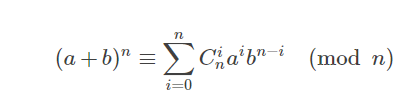
，然后除了i=0以及i=n时,Cin=1，其余的mod n等于0
那么x≡(b+ω）(p+1)/2就有
x2≡（b+ω)p+1≡（b+ω)p*(b+ω)
由第二个定理就有x2≡（bp+ωp)*(b+ω)
由费马小定理bp-1≡1 (mod p)以及定理1有x2≡（b-ω)*(b+ω)
最后 x2≡b2-ω2=b2-(b2-a)=a (mod p)
所以x≡(b+ω）(p+1)/2是x2Ξa(mod m)的解
剩下的为什么这个Fp2域的解是我们要求的解，我就不会证明了，可以看上面的最后那个博客，有提到，以及时间复杂度的分析。
然后在实际实现中，ω的作用就是在于（x1+y1ω)*（x2+y2ω) 时，类似实部的地方为x1*x2+y1*y2*ω2
所以直接可以让ω为b2-a,b的话就是通过随机数得到，这个期望值是2。
直接来一个裸题：http://acm.timus.ru/problem.aspx?space=1&num=1132
1 #include<cstdio> 2 #include<cstdlib> 3 #include<ctime> 4 struct Ima{ 5 int x,y; 6 }; 7 int p,w; 8 Ima muli(const Ima &i1,const Ima &i2){ 9 Ima ans; 10 ans.x=(i1.x*i2.x%p+i1.y*i2.y%p*w%p)%p; 11 ans.y=(i1.x*i2.y%p+i1.y*i2.x%p)%p; 12 return ans; 13 } 14 Ima powi(Ima a,int b){ 15 Ima ans; 16 ans.x=1,ans.y=0; 17 while(b){ 18 if(b&1) ans=muli(ans,a); 19 a=muli(a,a); 20 b>>=1; 21 } 22 return ans; 23 } 24 int poww(int a,int b){ 25 int ans=1; 26 a%=p; 27 while(b){ 28 if(b&1) ans=ans*a%p; 29 a=a*a%p; 30 b>>=1; 31 } 32 return ans; 33 } 34 int Cipolla(int n){ 35 if(p==2) return 1; 36 if(poww(n,(p-1)>>1)+1==p) return -1; 37 int a; 38 while(true){ 39 a=rand()%p; 40 w=((a*a%p-n)%p+p)%p; 41 if(poww(w,(p-1)>>1)+1==p) break; 42 } 43 Ima ans; 44 ans.x=a,ans.y=1; 45 ans=powi(ans,(p+1)>>1); 46 return ans.x; 47 } 48 int main(){ 49 int t,n,ans1,ans2; 50 srand(time(NULL)); 51 scanf("%d",&t); 52 while(t--){ 53 scanf("%d%d",&n,&p); 54 n%=p; 55 ans1=Cipolla(n),ans2=p-ans1; 56 if(ans1==-1) printf("No root "); 57 else if(ans1==ans2) printf("%d ",ans1); 58 else if(ans1<ans2) printf("%d %d ",ans1,ans2); 59 else printf("%d %d ",ans2,ans1); 60 } 61 return 0; 62 }
还有牛客多校的一题：Quadratic equation
1 #include<cstdio> 2 #include<cstdlib> 3 #include<ctime> 4 typedef long long ll; 5 const ll p=1e9+7; 6 struct Ima{ 7 ll x,y; 8 }; 9 ll w; 10 Ima muli(const Ima &i1,const Ima &i2){ 11 Ima ans; 12 ans.x=(i1.x*i2.x%p+i1.y*i2.y%p*w%p)%p; 13 ans.y=(i1.x*i2.y%p+i1.y*i2.x%p)%p; 14 return ans; 15 } 16 Ima powi(Ima a,ll b){ 17 Ima ans; 18 ans.x=1,ans.y=0; 19 while(b){ 20 if(b&1) ans=muli(ans,a); 21 a=muli(a,a); 22 b>>=1; 23 } 24 return ans; 25 } 26 ll poww(ll a,ll b){ 27 ll ans=1; 28 a%=p; 29 while(b){ 30 if(b&1) ans=ans*a%p; 31 a=a*a%p; 32 b>>=1; 33 } 34 return ans; 35 } 36 ll Cipolla(ll n){ 37 if(n==0) return 0; 38 if(n==1) return 1; 39 if(poww(n,(p-1)>>1)+1==p) return -1; 40 ll a; 41 while(true){ 42 a=rand()%p; 43 w=((a*a%p-n)%p+p)%p; 44 if(poww(w,(p-1)>>1)+1==p) break; 45 } 46 Ima ans; 47 ans.x=a,ans.y=1; 48 ans=powi(ans,(p+1)>>1); 49 return ans.x; 50 } 51 void solve(ll b,ll c){ 52 ll n=((b*b%p-4*c%p)%p+p)%p; 53 ll a=Cipolla(n),x,y; 54 if(a==-1){ 55 printf("-1 -1 "); 56 return ; 57 } 58 if(!((a+b)&1)) y=(a+b)/2,x=b-y; 59 else y=(a+b+p)/2,x=b+p-y; 60 x=(x+p)%p; 61 y=(y+p)%p; 62 if(x>y) printf("%lld %lld ",y,x); 63 else printf("%lld %lld ",x,y); 64 } 65 int main(){ 66 int t; 67 ll b,c; 68 srand(time(NULL)); 69 scanf("%d",&t); 70 while(t--){ 71 scanf("%lld%lld",&b,&c); 72 solve(b,c); 73 } 74 return 0; 75 }
然后补充一下关于勒让得的一些性质
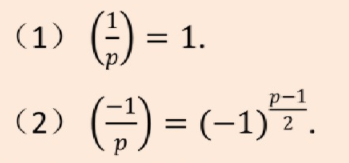
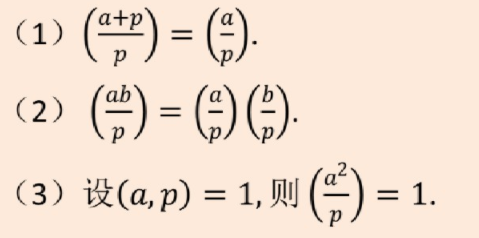
剩下的合数的还有其他补充内容就之后再更。