zoukankan html css js c++ java

图论之二分图相关内容

先来个360百科：

二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边(i，j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

那通俗来讲就是点能分成两个集合，同个集合的点之间没有边。

然后先来讲二分图的匹配吧。

先上博客：

Dark_Scope的趣写算法系列之--匈牙利算法

C20180630的二分图匹配——匈牙利算法和KM算法

齐鲁工业大学--栾琪的二分图详解----匈牙利算法+km算法+ Gale-Shapley---婚姻匹配算法算法+例题

然后先引入几个概念：

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点

最大匹配：匹配中的点数最多

完美匹配：图中所有的点都是匹配点。

二分图的最大匹配用的是匈牙利算法，上面的博客已经有非常详细的题解加解释，我就简单讲一下流程。

第一步：遍历一遍X集合所有未匹配的点x，由这个点去找增广路。

第二步：遍历一遍Y集合中没有在当前交错树中被访问过且跟当前的x有相连的点y

第三步：看y有没有匹配，没有的话，找到增广路，回溯回去修改。

第四步：y有匹配的话，看y匹配的那个x点能不能换一个匹配，也就是由它去找增广路。

第五步：交题，AC。

复杂度：

时间复杂度邻接矩阵:最坏为O(n^3)邻接表:O(mn)

空间复杂度邻接矩阵:O(n^2) 邻接表:O(m+n)

具体例题，因为之前做的没怎么保存，所以之后再补上了。

匈牙利算法，还有个优化，就是通过HK算法来优化到√nm的复杂度，

Fb_by的Hopcroft-karp 算法

其实这个算法就类似dinic中的分层图的思想，只不过是在二分图上分层。

加入优化后的流程：

第一步：遍历所有未匹配的X集中的点，加入队列，设深度为1.

第二步：由队列中的点去扩展分层，如果走到的y没有被访问过，它的深度等于x的深度+1，然后y没有匹配的，更新增广路的最低深度

第三步：y如果被匹配了，那么它匹配的x2点深度等于当前x的深度+1，并把它加入队列。

第四步：在处理出来的极大增广路集上跑匈牙利算法。

第五步：交题，AC。

这个算法的主要思路就是，每次都把最短多条不相交的增广路找出来，然后由此去增广，就不用像之前那样每次都只尝试的去找一条增广路。

至于为什么每次找最短的能对呢，是因为对一个点来说，增广路的长度增加，那跟它匹配的点也能增加（如果有的话），所以最短不影响答案的正确性。

具体例题，还是之后再补上了。

然后是要命的最大权匹配，先简单说一下什么是最大权匹配。

最大权匹配：每条边都带有边权，最大权匹配就是最终求得的匹配权值和最大，而不是匹配数最大，当然这两者不互斥。

然后挂上博客：

我不吃饼干呀 KM算法详解+模板

SixDayCoder 二分图的最佳完美匹配——KM算法

然后，首先根据题意，我们可以感觉得到，是可以通过最大费用最大流来解决的（也可以边权为负的最小费用最大流），建图的话，我们把源点与X集的点相连，汇点与Y集的点相连，都是流量为1，费用为0，而原先的X集的和Y集的边

流量为1，费用为边权。这时我们就建好了一个图，然而这个图还是存在一个Bug

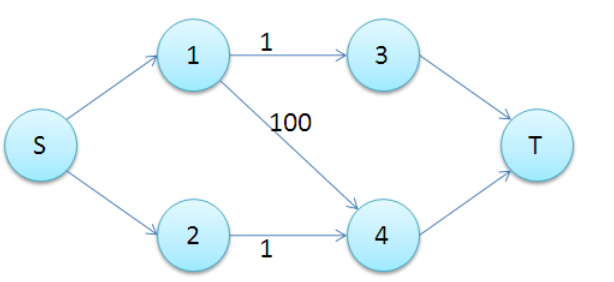
比如上面的图，跑出来的结果就是2，而不是100，因为最大费用最大流是在满足最大流的前提下然后才是最大费用的。

而解决方法很简单，我们把X集的点向汇点连一条费用为0流量为1的边，这样最终肯定是最大匹配，而走的是连汇点那条边的X集的点就是空匹配。

但这在处理UOJ80的二分最大权匹配仅仅只能过20组的样例，然后就T了，所以还是得用KM算法处理，下面我就结合两个博客来讲解下自己理解。

首先要知道KM算法是在完备匹配（完全匹配）的基础上去解决的，所以当两边点数不一样时，得补上点，而本来就是没有边连接的点就让它们边权为0就可以了。

然后KM算法一开始是给每个点都弄了个顶标，我直接引用大佬博客的了

那么我们把X集当成男生，Y集合当成女生，然后相连的边权是他们彼此的满意度的话，然后顶标的通俗说法就是男生女生对自己未来对象的期望值，那个求顶标值的函数就可以有一个通用的设定方法。

男生集的点的期望值就让他们是0，（只要是个女的就行，没有其他要求了），然后女生集的点的期望值我们就让她们是与她们相连的边的边权（也就是满意度）中最大的，（毕竟这是社会现状，人心所向）

也就是lx(x)=0,ly(y)=max(weight(xi,y)），这么一来就满足了lx(x)+ly(y)>=weight(x,y)

然后有一个相等子图的概念：

也就是相等子图中相连的男女的满意度刚好等于他们的期望值之和。

KM算法的可行性就基于以下定理。

定理：如果原图的一个相等子图中包含完备匹配，那么这个匹配就是原图的最佳二分图匹配。

证明：由于算法中一直保持顶标的可行性，所以任意一个匹配的权值之和肯定小于等于所有结点的顶标之和，则相等子图中的完备匹配肯定是最优匹配。

这里不知道怎么解释，换碟。走流程。

第一步：按照上面的方法，先设定好每个人的期望初始值。

第二步：让每个妹子去找对象（可以采用匈牙利算法），直到找到对象，找不到对象就通过调整期望值的方法，来调整相同子图，然后反复直至找到对象。

具体的调整方法就是：上一轮找对象的过程中，所涉及到的女生降低期望（为了生活），男生提高期望（被妹子追就飘了），

而具体降低的期望值就是，能让涉及到的女生找到一个为涉及到的男生做对象的最低值，也就是lx(i)+ly(j)-w(i,j)的最低值，其中i不曾在上一轮找对象的过程中涉及到，而j有被涉及了。

第三步：交题，AC。

第二步中降低了期望值就使得，更多的男的能加入相亲大潮。专业点的说法就是，上一轮匹配中涉及到就说明他们出现在增广路中，而我们是对在增广路中的男女同时加减上一个常量，那么对一对男女来说

他们本来都在增广路中，那么他们相应的期望值之和不变，下次还是能继续尝试匹配，

而男的在，女的不在的话，本来他们就不尝试匹配，现在女的期望不变，男的期望变高了，他们更加没有可能了，

男的不在，女的在的话，男的期望不变，女的期望变低，他们下一轮就有可能进行匹配了，而且就算因为这些匹配的加入，使得所以参与本次相亲的人对象的分配可能有了成功。

男的女的都不来，人家都没来相亲就不用管了。

实现上的话，可以用个数组来先求出lx(i)+ly(j)-w(i,j)的最低值，这样就不用去n²来求出，而看似这个优化能把n⁴的复杂度降到n³，但实际跑出来的鲜果并不是，还得是把dfs的匈牙利改成bfs的。

  1 //最小费用最大流zwk版本，最多20组样例 
  2 #include<cstdio>
  3 #include<queue>
  4 #include<algorithm>
  5 #include<cstring>
  6 using namespace std;
  7 typedef long long ll;
  8 const int N=1611,M=3e5+11,iinf=1e9+7;
  9 const ll linf=1e18+7;
 10 struct Side{
 11     int v,ne,w;
 12     ll val;
 13 }S[M<<1];
 14 bool vis[N];
 15 int s,t,sn,n1,n2,head[N],flow[N],pp[N];
 16 ll ansc,dis[N];
 17 void init(){
 18     sn=0;
 19     s=0;t=n1+n2+1;
 20     for(int i=s;i<=t;i++) head[i]=-1;
 21 }
 22 void add(int u,int v,int w,ll val){
 23     S[sn].w=w;
 24     S[sn].v=v;
 25     S[sn].val=val;
 26     S[sn].ne=head[u];
 27     head[u]=sn++;
 28 }
 29 void addE(int u,int v,int w,ll val){
 30     add(u,v,w,val);
 31     add(v,u,0,-val);
 32 }
 33 bool spfa(){
 34     for(int i=s;i<=t;i++){ 
 35         dis[i]=linf;
 36         vis[i]=false;
 37     }
 38     dis[t]=0;
 39     vis[t]=true;
 40     deque<int> q;
 41     q.push_back(t);
 42     while(!q.empty()){
 43         int u=q.front();
 44         q.pop_front();
 45         vis[u]=false;
 46         for(int i=head[u];~i;i=S[i].ne){
 47             int v=S[i].v;
 48             if(S[i^1].w>0&&dis[v]>dis[u]-S[i].val){
 49                 dis[v]=dis[u]-S[i].val;
 50                 if(!vis[v]){
 51                     vis[v]=true;
 52                     if(!q.empty()&&dis[v]<dis[q.front()])
 53                         q.push_front(v);
 54                     else q.push_back(v);
 55                 }
 56             }
 57         }
 58     }
 59     return dis[s]!=linf; 
 60 }
 61 int dfs(int u,int minf){
 62     if(u==t){
 63         vis[t]=true;
 64         return minf;
 65     }
 66     vis[u]=true;
 67     int flow=0,temp,v;
 68     for(int i=head[u];~i;i=S[i].ne){
 69         v=S[i].v;
 70         if(!vis[v]&&S[i].w>0&&dis[u]-S[i].val==dis[v]){
 71             pp[u]=v;
 72             temp=dfs(v,min(S[i].w,minf-flow));
 73             if(temp){
 74                 ansc+=S[i].val*temp;
 75                 S[i].w-=temp;
 76                 S[i^1].w+=temp;
 77                 flow+=temp;
 78             }
 79             if(flow==minf) break;
 80         }
 81     }
 82     return flow;
 83 } 
 84 void mfml(){
 85     int ans=0;
 86     ansc=0;
 87     while(spfa()){
 88         vis[t]=true;
 89         while(vis[t]){
 90             for(int i=s;i<=t;i++) vis[i]=false;
 91             ans+=dfs(s,iinf);
 92         }
 93     }
 94     printf("%lld
",-ansc);
 95 }
 96 int main(){
 97     int m,u,v;
 98     ll val;
 99     while(~scanf("%d%d%d",&n1,&n2,&m)){
100         init();
101         for(int i=1;i<=n1;i++){
102             addE(s,i,1,0);
103             addE(i,t,1,0); 
104         } 
105         for(int i=1;i<=n2;i++) addE(n1+i,t,1,0);
106         while(m--){
107             scanf("%d%d%lld",&u,&v,&val);
108             addE(u,n1+v,1,-val);
109         }
110         mfml();
111         for(int i=1;i<=n1;i++){
112             pp[i]=pp[i]==t ? 0 : pp[i]-n1;
113             printf("%d%c",pp[i]," 
"[i==n1]);
114         }
115     }
116     return 0;
117 }

最小费用最大流的尝试，T了

 1 //n4
 2 #include<cstdio>
 3 #include<algorithm>
 4 using namespace std;
 5 typedef long long ll;
 6 const int N=411;
 7 const ll inf=1e18+7;
 8 ll ex[N],ey[N],del[N],val[N][N];
 9 int nx,ny,vn,px[N],visx[N],visy[N];
10 bool aug(int u){
11     visy[u]=vn;
12     for(int i=1;i<=nx;i++){
13         if(visx[i]==vn) continue;
14         ll temp=ey[u]+ex[i]-val[u][i];
15         if(!temp){//是可行边才尝试匹配 
16             visx[i]=vn;
17             if(!px[i]||aug(px[i])){
18                 px[i]=u;
19                 return true;
20             }
21         }else del[i]=min(del[i],temp);
22     }
23     return false;
24 }
25 void km(){
26     //先预处理期望值 
27     for(int i=1;i<=nx;i++) px[i]=ex[i]=0;
28     for(int i=1;i<=ny;i++){
29         ey[i]=0;
30         for(int j=1;j<=nx;j++) ey[i]=max(ey[i],val[i][j]);
31     }
32     vn=0;
33     for(int j=1;j<=nx;j++) visx[j]=0;
34     for(int j=1;j<=ny;j++) visy[j]=0;
35     for(int i=1;i<=ny;i++){
36         for(int j=1;j<=nx;j++) del[j]=inf;
37         while(true){
38             ++vn;
39             if(aug(i)) break;//增广成功，当前女生找到对象，结束 
40             ll d=inf;
41             for(int j=1;j<=nx;j++) if(visx[j]!=vn) d=min(d,del[j]); //不在增广路中的男的，找到最小降低差值 
42             for(int j=1;j<=ny;j++) if(visy[j]==vn) ey[j]-=d;//在增广路中的女的降低期望 
43             for(int j=1;j<=nx;j++) if(visx[j]==vn) ex[j]+=d;//在增广路中的男的提高期望 
44             else del[j]-=d;//因为girl们的期望值降低，不在增广路的男生能找到对象所需值降低 
45         }
46     }
47 }
48 void solve(int n){
49     km();
50     ll ans=0;
51     for(int i=1;i<=n;i++) ans+=val[px[i]][i];
52     printf("%lld
",ans);
53     for(int i=1;i<=n;i++){
54         if(!val[px[i]][i]) px[i]=0;
55         printf("%d%c",px[i]," 
"[i==nx]);
56     }
57 }
58 int main(){
59     ll w;
60     int m,u,v,n;
61     while(~scanf("%d%d%d",&nx,&ny,&m)){
62         n=nx;nx=max(nx,ny);
63         for(int i=0;i<=ny;i++)
64             for(int j=0;j<=nx;j++) val[i][j]=0;
65         while(m--){
66             scanf("%d%d%lld",&v,&u,&w);
67             val[u][v]=w;
68         }
69         solve(n);
70     }
71     return 0;
72 }

n4?T了

  1 //bfsn3
  2 #include<cstdio>
  3 #include<queue>
  4 #include<algorithm>
  5 using namespace std;
  6 typedef long long ll;
  7 const int N=411;
  8 const ll inf=1e18+7;
  9 queue<int> q;
 10 ll ex[N],ey[N],del[N],val[N][N];
 11 int nx,ny,vn,px[N],py[N],pre[N],visx[N],visy[N];
 12 void init(){
 13     vn=0;
 14     for(int i=0;i<=ny;i++) py[i]=visy[i]=0;
 15     for(int i=0;i<=nx;i++) px[i]=visx[i]=0;
 16     for(int i=0;i<=ny;i++)
 17         for(int j=0;j<=nx;j++)
 18             val[i][j]=0;
 19 }
 20 bool aug(){
 21     int u,v;
 22     ll temp;
 23     while(!q.empty()){
 24         u=q.front();
 25         q.pop();
 26         for(int i=1;i<=nx;i++){
 27             if(visx[i]==vn) continue;
 28             temp=ey[u]+ex[i]-val[u][i];
 29             if(!temp){
 30                 pre[i]=u;
 31                 if(!px[i]){
 32                     for(int x=u,y=i,z;y;x=pre[y]){
 33                         z=py[x];
 34                         py[x]=y;
 35                         px[y]=x;
 36                         y=z;
 37                     }//跟带花树的类似，一样是匹配边非匹配边交替修改 
 38                     return 1;
 39                 }
 40                 visx[i]=vn;
 41                 if(visy[px[i]]!=vn){
 42                     visy[px[i]]=vn;
 43                     q.push(px[i]); 
 44                 }
 45             }else if(temp<del[i]){
 46                 pre[i]=u;
 47                 del[i]=temp;
 48             }
 49         }
 50     }
 51     return false;
 52 }
 53 void km(){
 54     for(int i=1;i<=ny;i++){
 55         ey[i]=0;
 56         for(int j=1;j<=nx;j++) ey[i]=max(ey[i],val[i][j]);
 57     }
 58     for(int i=1;i<=nx;i++) ex[i]=0;
 59     for(int i=1;i<=ny;i++){
 60         for(int j=1;j<=nx;j++){
 61             del[j]=inf;
 62             pre[j]=0;
 63         }
 64         while(!q.empty()) q.pop();
 65         q.push(i);
 66         visy[i]=++vn; 
 67         while(true){
 68             if(aug()) break;
 69             ll d=inf;
 70             for(int j=1;j<=nx;j++) if(visx[j]!=vn) d=min(d,del[j]);
 71             for(int j=1;j<=ny;j++) if(visy[j]==vn) ey[j]-=d;
 72             for(int j=1;j<=nx;j++) if(visx[j]==vn) ex[j]+=d;
 73             else if(del[j]<inf) del[j]-=d;
 74             //上面的跟dfs的处理一样 
 75             bool flag=false;
 76             for(int j=1;j<=nx;j++){//在调整了期望值后 
 77             //找到能参与进匹配的男生 
 78                 if(visx[j]==vn||del[j]!=0) continue;
 79                 if(!px[j]){
 80                     for(int x=pre[j],y=j,z;y;x=pre[y]){
 81                         z=py[x];
 82                         py[x]=y;
 83                         px[y]=x;
 84                         y=z;
 85                     }
 86                     flag=true;
 87                     break;
 88                 }
 89                 visx[j]=vn;
 90                 if(visy[px[j]]!=vn){
 91                     visy[px[j]]=vn;
 92                     q.push(px[j]); 
 93                 }
 94             }
 95             if(flag) break;
 96         }
 97     }
 98 }
 99 void solve(int n){
100     km();
101     ll ans=0;
102     for(int i=1;i<=n;i++) ans+=val[px[i]][i];
103     printf("%lld
",ans);
104     for(int i=1;i<=n;i++){
105         if(!val[px[i]][i]) px[i]=0;
106         printf("%d%c",px[i]," 
"[i==n]);
107     }
108 }
109 int main(){
110     ll w;
111     int m,u,v,n;
112     while(~scanf("%d%d%d",&nx,&ny,&m)){
113         n=nx;
114         if(nx<ny) nx=ny;
115         init();
116         while(m--){
117             scanf("%d%d%lld",&v,&u,&w);
118             val[u][v]=w;
119         }
120         solve(n);
121     }
122     return 0;
123 }

为啥这就n3了

还有个模仿叉姐的写法，没搞懂，时间效率上差不多，不过空间更优。

 1 //叉姐nb 
 2 #include<cstdio>
 3 #include<queue>
 4 #include<algorithm>
 5 using namespace std;
 6 typedef long long ll;
 7 const int N=411;
 8 const ll inf=1e18+7;
 9 queue<int> q;
10 ll ex[N],ey[N],del[N],val[N][N];
11 int nx,ny,vn,px[N],py[N],pre[N];
12 bool vis[N];
13 void init(){
14     vn=0;
15     for(int i=0;i<=ny;i++) py[i]=0;
16     for(int i=0;i<=nx;i++) px[i]=0;
17     for(int i=0;i<=ny;i++)
18         for(int j=0;j<=nx;j++)
19             val[i][j]=0;
20 }
21 void aug(int u){
22     for(int i=0;i<=nx;i++){
23         vis[i]=false;
24         del[i]=inf;
25     }
26     int x=0,y=0,v;
27     ll temp,d;
28     for(px[0]=u,vis[0]=true;px[x];vis[y]=true,x=y){
29         u=px[x];d=inf;
30         for(int i=1;i<=nx;i++){
31             if(vis[i]) continue;
32             temp=ey[u]+ex[i]-val[u][i];
33             if(temp<del[i]){
34                 pre[i]=x;
35                 del[i]=temp;
36             }
37             if(del[i]<d){
38                 y=i;
39                 d=del[i];
40             }
41         }
42         if(!d) continue;
43         for(int i=0;i<=nx;i++) if(vis[i]){
44             ex[i]+=d;
45             ey[px[i]]-=d;
46         }else del[i]-=d;
47     }
48     while(x){
49         y=x;
50         x=pre[x];
51         px[y]=px[x];
52     }
53 }
54 void km(){
55     for(int i=1;i<=ny;i++){
56         ey[i]=0;
57         for(int j=1;j<=nx;j++) ey[i]=max(ey[i],val[i][j]);
58     }
59     for(int i=1;i<=nx;i++) ex[i]=0;
60     for(int i=1;i<=ny;i++) aug(i);
61 }
62 void solve(int n){
63     km();
64     ll ans=0;
65     for(int i=1;i<=n;i++) ans+=val[px[i]][i];
66     printf("%lld
",ans);
67     for(int i=1;i<=n;i++){
68         if(!val[px[i]][i]) px[i]=0;
69         printf("%d%c",px[i]," 
"[i==n]);
70     }
71 }
72 int main(){
73     ll w;
74     int m,u,v,n;
75     while(~scanf("%d%d%d",&nx,&ny,&m)){
76         n=nx;
77         if(nx<ny) nx=ny;
78         init();
79         while(m--){
80             scanf("%d%d%lld",&v,&u,&w);
81             val[u][v]=w;
82         }
83         solve(n);
84     }
85     return 0;
86 }

nbnbnbnb

最后就是这个

证明可以看上面博客，这里我就只把概念和解决方法提取出来。

最小点覆盖：二分图中，选取最少的点数，使这些点和所有的边都有关联（把所有的边的覆盖），叫做最小点覆盖。

解决方法：最小点覆盖数 = 最大匹配数

最小路径覆盖：这跟一般图的是同一个。给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。

解决方法：对于G中每一个节点x，建立节点x1，x2。若x- >y存在边，则x1与y2之间连一条无向边，求这个二分图的最大匹配数即可。然后，最小路径覆盖=|G|-最大匹配数

最大独立集：独立集是指图G中两两互不相邻的顶点构成的集合。最大，就是点数最多。

解决方法：最大独立集=总数-最小覆盖集

例题之后补上。

查看全文

相关阅读:
kubenetes-学习
 k8s-字段
 Spring Boot集成mongodb
synchronized关键字
 Scala手记
 Python数据结构&封装解构
 Scala基础之集合
 Scala基础之集合常用方法
 Scala（2.12）之collection基本操作
 Scala基础之集合（数组）

原文地址：https://www.cnblogs.com/LMCC1108/p/11541015.html