题意:给n*m的地图,入口是(0,0),出口是(n,m),其中有k个监视器,坐标是(xi,yi),监视半径是r,问一个人能不能不被监视到,从起点到终点。
如果不能走到终点,无非便是监视范围把路全堵死了,所以开始的想法便是计算几何题,看多个圆能不能把横的和竖的都给覆盖了,但很明显行不通,然后想了想觉得这可以转换成一个图的题。
我们把每个监视器看出点,然后遍历每个监视器跟它相交(相切,包含)的其他点,已经看一下这个圆会涉及到那些边界。然后会把路封死的组合便是,上边界跟左边界,上边界跟下边界,右边界跟下边界,右边界跟左边界。
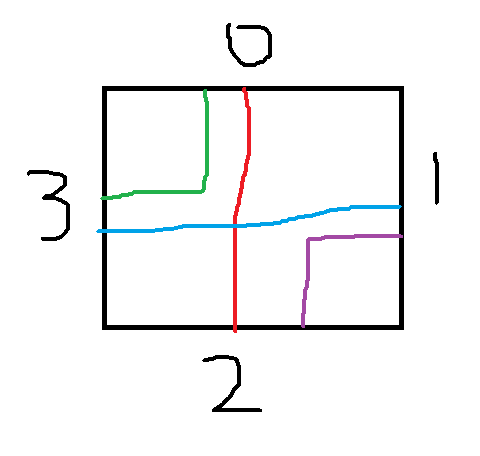
(也就是上图中五颜六色的线)
所以我们就看每个连通块涉及的边界组合中有没有上述边界。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=1e3+11,M=N*N+11; 5 struct Side{ 6 int v,ne; 7 }S[M<<1]; 8 bool vis[N],book[10]; 9 int n,m,k,sn,head[N],xx[N],yy[N],rr[N]; 10 void init(){ 11 sn=0; 12 for(int i=0;i<k;i++){ 13 head[i]=-1; 14 vis[i]=false; 15 } 16 } 17 void add(int u,int v){ 18 S[sn].v=v; 19 S[sn].ne=head[u]; 20 head[u]=sn++; 21 } 22 int pf(int x){ 23 return x*x; 24 } 25 bool judge(int x,int y){ 26 return pf(xx[x]-xx[y])+pf(yy[x]-yy[y])<=pf(rr[x]+rr[y]); 27 } 28 void dfs(int u){ 29 vis[u]=true; 30 //0 1 2 3分别代表上 右 下 左 边界 31 if(xx[u]-rr[u]<=0) book[0]=true; 32 if(yy[u]+rr[u]>=m) book[1]=true; 33 if(xx[u]+rr[u]>=n) book[2]=true; 34 if(yy[u]-rr[u]<=0) book[3]=true; 35 for(int i=head[u],v;~i;i=S[i].ne){ 36 v=S[i].v; 37 if(!vis[v]) dfs(v); 38 } 39 } 40 bool solve(){ 41 for(int i=0;i<k;i++){ 42 if(vis[i]) continue; 43 for(int j=0;j<4;j++) book[j]=false; 44 dfs(i); 45 if((book[0]||book[1])&&(book[2]||book[3])) return false; 46 } 47 return true; 48 } 49 int main(){ 50 while(~scanf("%d%d%d",&n,&m,&k)){ 51 init(); 52 for(int i=0;i<k;i++) scanf("%d%d%d",&xx[i],&yy[i],&rr[i]); 53 for(int i=0;i<k;i++) 54 for(int j=i+1;j<k;j++) if(judge(i,j)){ 55 add(i,j); 56 add(j,i); 57 } 58 if(solve()) printf("S "); 59 else printf("N "); 60 } 61 return 0; 62 }
