【POJ2778】DNA Sequence 【AC自动机，dp，矩阵快速幂】

题意

  题目给出m(m<=10)个仅仅由A,T,C,G组成的单词(单词长度不超过10)，然后给出一个整数n(n<=2000000000)，问你用这四个字母组成一个长度为n的长文本，有多少种组成方法可以使得它不含任何一个给出的单词。

分析

  当时一看以为是跟训练指南上（UVA11468）一样的题，感觉只有四个字母并且单词数量和长度也比较小，但是一看给出的n有点懵逼。如果再按照书上建立AC自动机以后直接跑DP的方法肯定是不行了。然后我们就要用到，递推利器，矩阵快速幂。

  我们还是按照套路先把AC自动机建出来，然后将每个单词结点设为非法结点，题目变成在AC自动机中走n步不通过非法结点的方案数。然后设f[i][j]是当前在结点i，已经走了j步，且未走过非法结点的方案数。然后怎么转移呢？

  f[i][j]=A(0,i)*f[0][j-1]+A(1,i)*f[1][j-1]+...+A(sz-1,i)f[sz-1][j-1]。其中A(i,j)的含义就是从i到j有几条直接连接的边。那么将这个dp方程拆开来看

  

  f0[i]=A(0,0)*f[0][i-1]+A(1,0)*f[1][i-1]+....+A(sz-1,0)*fsz-1[i-1]

  f1[i]=A(0,1)*f[0][i-1]+A(1,1)*f[1][i-1]+....+A(sz-1,1)*fsz-1[i-1]

  .

  .

  fsz-1[i]=A(0,sz-1)*f[0][i-1]+A(1,sz-1)*f[1][i-1]+...+A(sz-1,sz-1)*fsz-1[i-1]

 然后根据这个我们就很好建立转移矩阵

 *

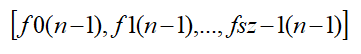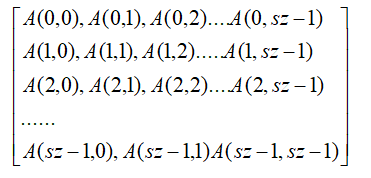
  （第一次学会用公式编辑器不过好像还是贼丑）

   然后建立这个大的转移矩阵，矩阵的(i,j)为结点i到结点j的直接路径的条数，然后跑一个矩阵快速幂。 

   最后把从0到sz-1结点的f(n)的值全部加起来就是答案了。

    对了这个题需要用long long

   下面是代码

   

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#include <map>

using namespace std;
const int maxnode=1100;
const int MOD=100000;
map<char,int>M;
struct AC_Automata{
    int ch[maxnode][4],f[maxnode],last[maxnode],val[maxnode],match[maxnode];
    int sz;
    int idx(char c){
        return M[c];
    }
    void init(){
        sz=1;
        memset(ch[0],0,sizeof(ch[0]));
        memset(match,0,sizeof(match));
        val[0]=0;
    }
    void insert(char *s){
        int n=strlen(s),u=0;
        for(int i=0;i<n;i++){
            int c=idx(s[i]);
            if(!ch[u][c]){
                ch[u][c]=sz;
                memset(ch[sz],0,sizeof(ch[sz]));
                val[sz++]=0;
            }
            u=ch[u][c];
        }
        val[u]=1;
        match[u]=1;
    }
    void getFail(){
        queue<int>q;
        last[0]=f[0]=0;
        for(int i=0;i<4;i++){
            int u=ch[0][i];
            if(u){
                q.push(u);
                f[u]=last[u]=0;
            }
        }
        while(!q.empty()){
            int r=q.front();q.pop();
            for(int i=0;i<4;i++){
                int u=ch[r][i];
                if(!u){
                    ch[r][i]=ch[f[r]][i];
                    continue;
                }
                q.push(u);
                int v=f[r];
                while(v&&!ch[v][i])v=f[v];
                f[u]=ch[v][i];
                match[u]|=match[f[u]];
            }
        }
    }
}ac;
const int maxN=101;
struct Matrix{
    long long a[maxN][maxN];
    void init(){
        memset(a,0,sizeof(a));
        for(int i=0;i<ac.sz;i++)
            a[i][i]=1;
    }
};
Matrix mul(Matrix a,Matrix b){
    Matrix res;
    for(int i=0;i<ac.sz;i++){
        for(int j=0;j<ac.sz;j++){
            res.a[i][j]=0;
            for(int k=0;k<ac.sz;k++){
                res.a[i][j]+=a.a[i][k]*b.a[k][j];
                res.a[i][j]%=MOD;
            }
        }
    }
    return res;
}
Matrix qpow(Matrix a,int k){
    Matrix res;
    res.init();
    while(k){
        if(k%2)res=mul(res,a);
        a=mul(a,a);
        k/=2;
    }
    return res;
}
int n,m;
char s[30];

int main(){
    M['A']=0,M['C']=1,M['T']=2,M['G']=3;
    ac.init();
    scanf("%d%d",&m,&n);
    for(int i=1;i<=m;i++){
        scanf("%s",s);
        ac.insert(s);
    }
    ac.getFail();
    Matrix A;
    for(int i=0;i<ac.sz;i++){
            if(!ac.match[i])
        for(int j=0;j<4;j++){
            int u=ac.ch[i][j];
            if(!ac.match[u])
            A.a[i][u]++;
        }
    }
    /*for(int i=0;i<ac.sz;i++){
        for(int j=0;j<ac.sz;j++){
            printf("%d ",A.a[i][j]);
        }
        printf("
");
    }*/

    Matrix S;
    S.a[0][0]=1;
    Matrix ANS;
    ANS=qpow(A,n);
    ANS=mul(S,ANS);
    long long ans=0; 
    for(int i=0;i<=ac.sz;i++)
        ans+=ANS.a[0][i];
    printf("%d
",ans%MOD);
return 0;
}