5-ML的可行性（2）

本节主题：基于上一节的铺垫，继续深入研究当M无穷大时如何保证fesibilty of ml

1. Learnning中涉及的两个关键问题：

• 保证 $ E_{in} approx E_{out} $
• 保证 $ E_{in} approx 0 $

• 第二行很好理解，就是找一个合适的hypothesis h,使的(E_{in})达到足够小，这个h即为所求的g，这对应了Training过程
• 第一行其实描述了ML可行性的一个很重要的条件，可由Testing过程来表达出来，但却不是由Testing过程所决定。下面首要的就是分析第一行的成立条件。

2. BAD DATA问题的解决：

1. 上一节我们讨论得到一个不等式：
   (mathbb{P}[| E_{in}(g) - E_{out}(g) | gt epsilon] leq 2cdot M cdot exp(-2epsilon ^2N))
   这就存在一个两难问题：

   

   • M太小，就能保证$ E_{in} = E_{out}(，但是由于)|mathcal{H}|(太小，不一定找得到一个`hypothesis h`使得) E_{in} = 0$ ；
   • M太大，由于(|mathcal{H}|)很小，hypothesis选择较多，很容易找到一个hypothesis h使得$ E_{in} = 0$ ，但是不能保证$ E_{in} = E_{out}$；
   • 这个M的取值非常关键。

2. BAD DATA的发生概率和N、M关系重大，N可以人为控制【样本点足够大即可】，但M是(|mathcal{H}|)，却不一定可以人为控制：像PLA的(|mathcal{H}|)天生就是infinite。但是PLA的实际效果却依然excellent，说明M即使无穷大，依然有可能实现 $ E_{in} = E_{out}, PAC $

3. 根据Hoffiled-Iquality，我们得到:
   (mathbb{P}[| E_{in}(g) - E_{out}(g) | gt epsilon] leq 2cdot M cdot exp(-2epsilon ^2N))
   那么当M无穷大时，BAD发生的概率有可能会很大，这样机器学习就没有意义【BAD 发生就意味着 $ E_{out} ; and ; E_{in}$ 相差巨大，根本不能用 (E_{in}) 来近似代替 (E_{out}) ，那我们通过Train找到的g不能近似代替f】

4. 但是，上述的不等式真的合理吗？考虑上述不等式的推导过程：记 H 中第m个hypothesis遇到bad sample为事件$ mathcal{B}m:|E{in}(h_m) - E_{out}(h_m)| gt epsilon(，则 `H`遇到`bad sample`的概率为其所有`hypothesis`遇到`bad sample`概率的【联合概率】。考虑一种极端情况：如果每个方程遇上`bad sample`这件事是【互相独立】的，则 `H` 遇上`bad sample`的概率是`H`的各`hypothesis`遇上`bad sample`的概率之和，因此他们的【联合概率】一定小于或等于各个事件单独发生的【概率之和】，即： )mathbb{P}[mathcal{B}_1 or mathcal{B}_2 or ... or mathcal{B}_M] leq mathbb{P}[mathcal{B}_1] + mathbb{P}[mathcal{B}_2] + ... + mathbb{P}[mathcal{B}_M]$

5. 但是，我们通过分析hypothesis的相似性，发现了一个规律：

   

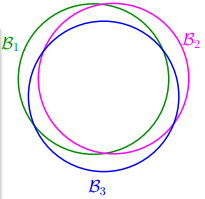
   其实无限的hypothesis其实是互相重叠的，不存在【相互独立】，即上式等号是取不到的。

6. 至此，我们了解到，之前对BAD的union-bound是一个over-estimating，所以应该找一个“更紧”的upper-bound。我们理想的upper-bound是一个仅与输入样本点个数N有关的polynomial函数【polynomial函数即使趋向无穷大，增长速度也可以被限制】。

7. 换言之，可以通过把infinite的hypothesis sets进行分组，可以得到definite个effictive hypothesis grounp，以下为几个例子：
   xxx

8. 换言之，我们如果能将M替换为|group|，并且这个有限的|group|还是poly(N)，那么就能够有效降低BAD DATA的发生概率，进而 (E_{in} approx E_{out}, g approx f) ，再去找满足 (E_{in} approx 0) 的h才有意义。 所以，我们下面推导有两个方向：第一，证明|group|的确是poly(N)；第二，|group|可以代替M。

3. 方向1：证明|group|是poly(N)：

对任意一个h在输入了N个样本点的条件下，找到这个h的group。显然N个样本点的不同组合将会产生不同的效果，作如下定义：

1. dichtomy：前期可以简单地理解为某一个二分类器产生的一个分类结果，比如PLA所学习到的一根分界线或者分界超平面。

2. 一个dichtomy = 一个 effictive h group。关于effictive h group简单的说，就是按照上述的介绍，虽然h的搜索空间(mathcal{H})的大小(mathcal{|H|})(记做M)，是无穷大的，但是因为所有h对数据集D产生的分类结果是有限的，【根据分类结果对全部h做分组】，得到的group一般是有限的。【同属于这一个group的hypothesis h都只能产生同一个dichtomy】，这可以理解为一个聚类：根据【分类直线能产生的分类结果】这个属性对【所有分类直线】做聚类。

3. 对上面两点举例说明，以 2D percetrons为例：

   • N=1：
     

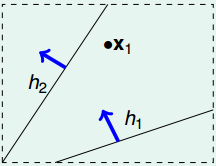
   • N=2：
     

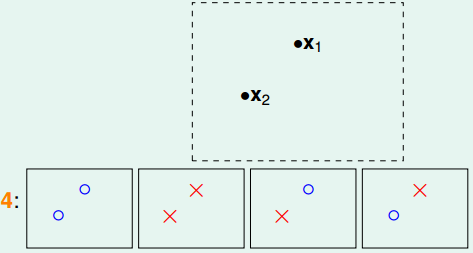
   • N=3：
     

     

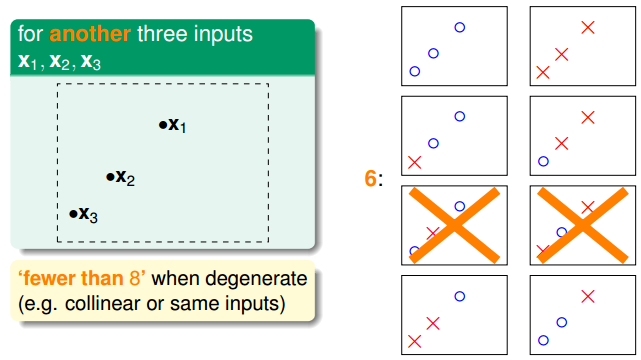
   • N= 4：
     

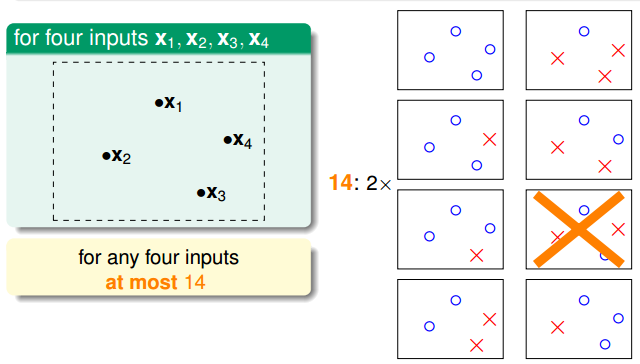
     由上图也可以看出：属于同一个group的每条直线，他们将【同时】遇到或不遇到bad sample，由于之前那个union bound是基于【每一条直线独立】的假设下的，因此H遭遇bad sample的概率明显被夸大了。所以，我们应该把不等式改写为：
     $ mathbb{P}[|E_{in}(g)-E_{out}(g)|gt epsilon]leq 2cdot effective(N)cdot exp(-2epsilon^2N) $

4. 同样的N个样本点，输入组合不同，产生的dichtomy也不同，如上图中：3-input的2D perceptrons，如果三点组成三角形，有8个dichtomy，如果是三点共线，那就只有6个dichtomy。

5. 为了屏蔽【相同数目】输入样本点的【组合差异】对group的影响，我们对|group|取一个upper-bound，即取 $ max{|group|} $ 。先定义
   $ H(x_1, x_2 ...x_N) = {dichtomies}(，当前)x_1, x_2 ...x_N$是N-inputs的一种组合方式。然后对 (H(x1, x2 ...)) 取一个upper-bound，记为增长函数grow function， (m_h = max{ |H(x_1,x_2 ...)|, x_1,x_2 in X }) ，问题转化为：证明这个 (m_h) 是poly(N)，(m_h)即上一个不等式中的(effective(N))。

6. 从具体实例分析分析(m_h)：

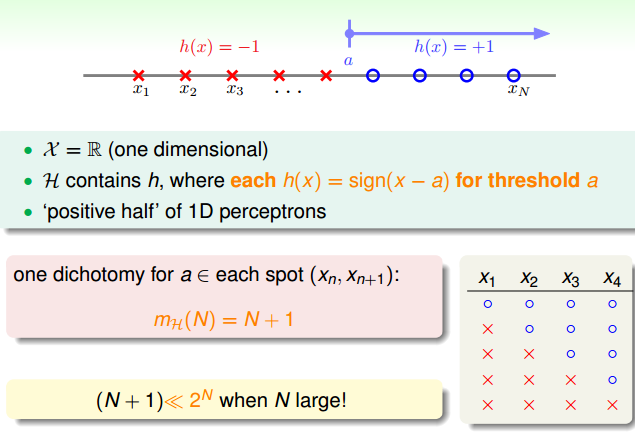
   • positive rays:
     

   • positive interval：
     

   • convex sets:
     

     

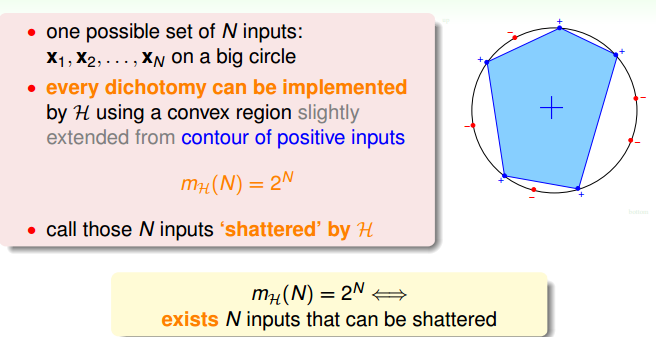
   • 2D perceptrons：之前有N=1,2,3,4的例子，更多规律，下面再讨论

7. 由上发现N较小的时候， (m_h) 一般都是 (2^N) ，即这个 (m_h) 是指数函数的；而增长到了某一个N的阈值后， (m_h) 会小于 (2^N) ，终于看到了poly(N)的影子。进而我们需要精密观测这个N的阈值。这个阈值就是一个Break point。【因为后面还会发现，break point不止一个】

   关于break point

   • break point 是什么？
     记k是某时刻样本点数目，如果 $ m_h(k-1) = 2^{k-1}, ; m_h(k)<2^{k} $ ，那么k就是h的第一个break point。它表达了h的一个信息：当(N<K)，【至少】能找到一个含N个样本点的input组合X，这时候h的 (m_h) 是 (2^N) ；而 (N ge K) 开始，所有的包含N个样本点的组合输入 (X') 对应的 (m_h) 都是小于 (2^N) 。换言之，我们终于找到了一个可能是poly(N)的 (m_h) 【|group|的upper-bound】。
   • break point的作用：

   • 一旦 (N<K) ，那么|group|都不是poly(N)；但是若 (N ge K)，那么【至少】存在一个h的|group|就有可能是poly(N)。那么我们的下一步目标就转化成：找到一个h的break point。
   • 但是问题又来了，那么多的h，虽然都输入同一个大小为N的样本点集合X，但还是要计算下每一个的grow _function 即 (m_h) 比较麻烦，这里我们受到上次定义grow _function的启发：为所有h的 (m_h) 做一个upper-bound，记做B(N，K)。它的原理是，通过对h设置break point k，bound住了当输入了N个样本点的【所有h】的grow _function(h,N)；
   • 它的深刻内涵是：只要我知道任意一个h的输入样本点数目N【而不用管这个N个点将组合成啥样】，以及这个h的break point【而不用管这个h到底长什么样子，因为不同h的break point有可能相同】，那么我就能得到这个h的|group|的upper-bound的uper-bound
   • 注意：之所以能忽略样本集的具体组合形式和具体h的形式的背后原因是：我们做了两次upper-bound，等于把BAD DATA的bound放大了两次】。下一步我们要做的就是，怎么写出这个B(N,K)

   • 牢牢记住：

   • break point是说：
     对于所有的的h，都无法产生 (2^N) 个dichtomy【比如h是2D-perceptrons，N为4时，不管N个点是任意一种组合的input方式，都最多只能产生14种dichtomy，小于 (2^4) ，所以4就是2D-perceptrons的一个break-point】；
   • non-break point是指:
     总能找到【至少】一个h，在面对【至少】有一个合适的N个样本点的某个输入组合input时，能产生 (2^N) 的dichtomy，【比如对于h是2D perceptrons，N为3时：3个点组合成三角形就是8个dichtomy，但是三点成线就只有6个dichtomy，的确能找到【至少】一个h和一个N-input，能产生2^3个dichtomy，所以这个3就是2D-perceptrons的一个non-break point】

8. 定义B(N,K)：(B(N,K) = max{m_h(N)}, s.t. ; break ; point = K)，即通过设置break point 为K屏蔽了一批hypotheses h的(m_h(N))的差异，借助K这个关键特点就代表了这一类hypotheses h，并通过取uppper-bound，代表了这一批hypotheses h的(m_h)。就求解B(N,K)这个问题，林轩田从2D percetron这个具体案例出发，导出了一个二维表格(如下图)。分析了B(N，K)的长相。直接贴结论：

[B(N,1) = 1 \ B(N,K) = 2^K, N<K \ B(N,K) = 2^K -1, N=K \ B(N,K) le B(N-1,K) + B(N-1,K-1), ; N>K ]

9. 如上，比较麻烦的是：N>K时的B(N,K)不存在一个准确的表达式，而是得到了它的upper-bound表达式。通过数学归纳法，最后得到 $B(N,K) le sum_{i=0}^{K-1} {N-1 choose i}, ; where N>K $
   对上式做一次放大简化，得到 (B(N,K) = o(N^{K-1}))

10. 再次梳理下我们推导的过程：
    $ |H| o |group| ;of ;h o m_h o B(N,K) o o(N^{K-1}) $
    有三次放大：

    1. h的|group|和N个样本点的组合形式有关，所以取了max{|group_i|}即grow_function(h,N)来屏蔽了N个样本点X的组合差异，这是第一次upper-bound
    2. grow_function(h,N)与h的具体形式有关，所以再次取了个max {grow_function(h_i,N)}，即只需知道了k【而不需要知道这个k对应的h究竟是哪一个】，就能知道【所有h】的|group|的upper-bound的upper-bound
    3. 对B(N,K)的表达式做了渐进分析，类比数据结构中的大o算法分析，直接取o(N^K)，简化了分析过程

4. 方向2：证明|group|的确可以代替|H|：

其实从一开始我们找|group|代替|H|的时候，就做了个假设：|group|可以代替|H|，但这个假设只是出于直觉，并没有严格的数学证明“可以代替”，及严格的代替公式。下一步就是做这个工作：怎么从数学上证明h的|group|确实可以替代h的总共搜索空间|H|，详见下一节。