这次，我们来继续学习博弈论的知识。今天我们会学习更多的基础模型，以及SJ定理的应用。
首先，我们来看博弈论在DAG上的应用。首先来看一个小例子：在一个有向无环图中，有一个棋子从某一个点开始一直向它的出点移动，双方轮流操作，无法操作者输，问是否先手必胜。
考虑一下我们之前的Nim游戏，如果我们把后继状态看成后继点的话，不难发现Nim游戏的互相转移也是一个DAG。因此，DAG上出度为0的点的sg值为0，再用上一篇博客提到的mex操作来求每个点的值就可以了（注意，这并不是一个“大”子图，不能拆成子游戏，因此不能异或了！）。在图上的递推操作是O(n)的，按照逆向拓扑序递推即可；如果有向无环图有多个，又怎么办呢？那么显然这个时候就可以异或了，直接计算即可。
接下来，我们来看一种Anti-SG游戏。顾名思义，这种游戏和一般的SG函数游戏不太一样：在这种游戏中，最后不能行动的人反而是赢家。那么现在怎么判断一个状态是N-Position（必胜）还是P-Position（必败）呢？
首先，很显然，如果有奇数个大小为1的石子堆，则先手必败；如果有偶数个，则先手必胜。
接着，我们从最简单的情况开始考虑，石子堆全是1的状态，肯定是由恰好有一个石子堆大于1个的状态走过来的
那么，谁拿到了这个状态，谁就能获胜。因为拿到这个状态的人可以通过控制最大那堆石子剩下的个数（1个或者0个）来使自己必胜
那么我们继续考虑。如果有一个人可以拿到这个先手必胜的状态，他一定是在初始状态是就“先手必胜”了。而初始状态的“先手必胜”和上一条的“先手必胜”意义不同：这里的初始状态先手必胜，指的是他能控制游戏的走向，从而使自己能拿到想要的状态，因此这里的“先手必胜”和Nim游戏一样，要求子游戏异或和大于0即可；而在拿到上述恰好有一个石子堆大于1个的状态之后，他一定是必胜的。
因此，只要初始的石子状态不是全为1，我们仍然可以用Nim的异或和做法来判断；而当状态全是1时，我们直接根据堆数奇偶判断即可。上面这些东西的学名就叫做“SJ定理”。如果不是取石子游戏，而是其他不确定sg计算方法的游戏（有向图游戏，台阶游戏……均可），我们可以先假设不能移动者赢，求出sg函数计算式，再利用SJ定理转化求解。
接下来，我们再来看一种新游戏模型：Muitl-SG游戏。这种游戏允许取走某些东西后，使原游戏呗分成几个新游戏。我们来看一道小例题：有n排石子，每次要从其中的一排中取出相邻的两个石子。无法操作者输。
这种问题如何操作呢？不难发现，在取走这两个石子后，原来的大游戏的后继状态变成了2个（或1个）子游戏。而我们知道，在符合条件时，异或可以对子游戏进行加和操作。所以，这个大游戏的后继状态的sg值，就是这个后继游戏状态中新产生的石子堆sg值的异或和，然后我们对后继状态的sg值再取异或和，就得到了这个大游戏状态的sg函数值。
我们再看一个更加复杂一点的游戏：Every-SG游戏。这种游戏除了是输赢的博弈之外，还是时间的博弈。我们看一道小例题：
有n个同时进行的游戏，每次都必须在还未结束的游戏中进行一步操作，不能在任何游戏里操作的人输。很明显，这个游戏的胜利在于不断在必胜的游戏中续命拖长时间，在必败的游戏里速战速决。那么我们可以在递归搜索时额外加入如下的语句，维护从这个游戏状态开始，最长的持续时间：
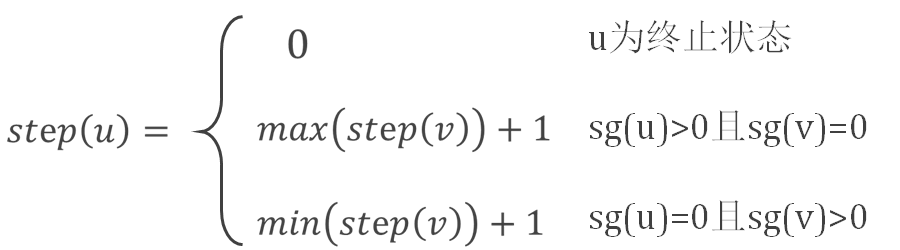对于必胜状态的步数要最大化，必败状态的步数要最小化，双方都是如此。
显然，先手必胜局面的步数一定是奇数，所以所有游戏中，最长步数若是奇数，先手必胜，否则先手必败。
今天我们介绍了4种博弈论的经典模型，并且还引入了SJ定理这一新的工具。下一次，我们会结合不同模型的经典例题来继续了解博弈论这个神奇的知识点。希望我的博文给你带来了帮助~:)