1.什么是卷积
在图像上滑动,取与卷积核大小相等的区域,逐像素做乘法然后相加
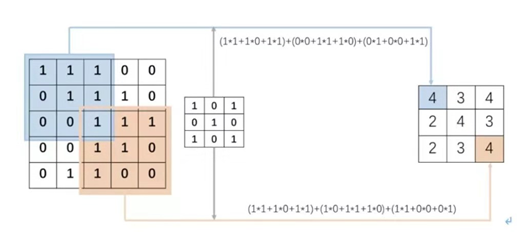
例如原始图像大小是5*5,卷积核大小是3*3。首先卷积核与原始图像左上角3*3对应位置的元素相乘求和,得到的数值作为结果矩阵第一行第一列的元素值,然后卷积核向右移动一个单位(即步长stride为1),与原始图像前三行第2、3、4列所对应位置的元素分别相乘并求和,得到的数值作为结果矩阵第一行第二列的元素值,以此类推。
故卷积就是:一个核矩阵在一个原始矩阵上从上往下、从左往右扫描,每次扫描都得到一个结果,将所有结果组合到一起得到一个新的结果矩阵。
2.为什么用卷积来学习
图像都是用方形矩阵来表达的,学习的本质就是要抽象出特征,以边缘检测为例。它就是识别数字图像中亮度变化明显的点,这些点连接起来往往是物体的边缘。
传统的边缘检测常用的方法包括一阶和二阶导数法,本质上都是利用一个卷积核在原图上进行滑动,只是其中各个位置的系数不同,比如3*3的sobel算子计算x方向的梯度幅度,使用的就是下面的卷积核算子。
如果要用sobel算子完成一次完整的边缘检测,就要同时检测x方向和y方向,然后进行融合。这就是两个通道的卷积,先用两个卷积核进行通道内的信息提取,再进行通道间的信息融合。
这就是卷积提取特征的本质,而所有基于卷积神经网络来学习的图像算法,都是通过不断的卷积来进行特征的抽象,直到实现网络的目标。
3,卷积神经网络的优势在哪?
前面说了全连接神经网络的原理和结构上的缺陷,而这正好是卷积的优势。
(1) 首先是学习原理上的改进,卷积神经网络不再是有监督学习了,不需要从图像中提取特征,而是直接从原始图像数据进行学习,这样可以最大程度的防止信息在还没有进入网络之前就丢失。
(2) 另一方面是学习方式的改进。前面说了全连接神经网络一层的结果是与上一层的节点全部连接的,100×100的图像,如果隐藏层也是同样大小(100*100个)的神经元,光是一层网络,就已经有 10^8 个参数。要优化和存储这样的参数量,是无法想象的,所以经典的神经网络,基本上隐藏层在一两层左右。而卷积神经网络某一层的结点,只与上一层的一个图像块相连。
用于产生同一个图像中各个空间位置像素的卷积核是同一个,这就是所谓的权值共享。对于与全连接层同样多的隐藏层,假如每个神经元只和输入10×10的局部patch相连接,且卷积核移动步长为10,则参数为:100×100×10×10,降低了2个数量级。
又能更好的学习,参数又低,卷积神经网络当然是可以成功了。
4.卷积神经网络的核心基础概念
在卷积神经网络中,有几个重要的基本概念是需要注意的,这在网络结构的设计中至关重要。
(1) 感受野
直观上讲,感受野就是视觉感受区域的大小。在卷积神经网络中,感受野是CNN中的某一层输出结果的一个元素对应输入层的一个映射,即feature map上的一个点所对应的输入图上的区域,具体示例如下图所示。
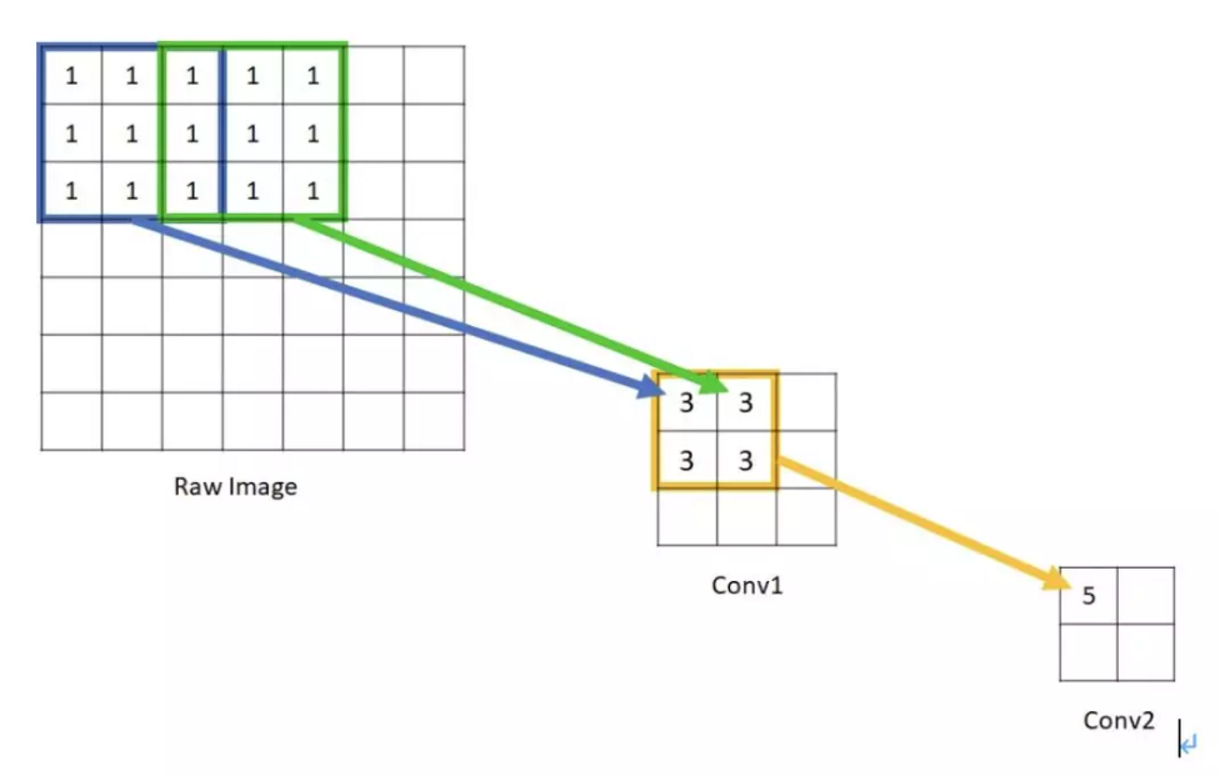
如果一个神经元的大小是受到上层N*N的神经元的区域的影响,那么就可以说,该神经元的感受野是N*N,因为它反映了N*N区域的信息。在上图conv2中的像素点5,是由conv1的2*2的区域计算得来,而该2*2区域,又是由raw image中5*5的区域计算而来,所以,该像素的感受野是5*5。可以看出感受野越大,得到的全局信息越多。在物体分割,目标检测中这是非常重要的一个参数。
(2) 池化
有了感受野再来解释池化(pooling)也很简单,上图的raw image到conv1,再到conv2,图像越来越小。每过一级就相当于一次降采样,这就是池化。池化可以通过步长不为1的卷积实现,也可以通过pool直接插值采样实现,本质上没有区别,只是权重不同。
通过卷积获得了特征之后,下一步则是用这些特征去做分类。理论上讲,人们可以把所有解析出来的特征关联到一个分类器,例如softmax分类器,但计算量非常大,并且极易出现过度拟合(over-fitting)。而池化层则可以对输入的特征图进行压缩,一方面使特征图变小,简化网络计算复杂度;一方面进行特征压缩,提取主要特征。
一般而言池化操作的池化窗口都是不重叠的,所以池化窗口的大小等于步长stride。如下图所示,采用一个大小为2*2的池化窗口,max pooling是在每一个区域中寻找最大值,这里的stride=2,最终在原特征图中提取主要特征得到右图。

除此之外,还有卷积核的大小,卷积的步长,通道的边界填充值等等,都是很好理解的基本概念。
一般的,卷积核边长大小F为奇数:
1、方便padding = same卷积操作,左右(上下)两边对称补零;
2、奇数卷积核有中心像素,便于确定卷积核的位置。
被卷积对象的大小为n*n,卷积核大小为k*k,padding幅度为(k-1)/2
如何计算加padding之后的新合成图的(w,h)?
w=h=n+2p-f+1
卷积后的输出为n+2*(k-1)/2-k+1=n,即卷积输出为n*n,保证了卷积前后尺寸不变
如何计算无padding新合成图的(w,h)?
w=h=n-f+1