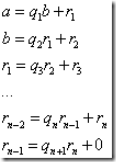数论概论——第五章

这章讲的是 整除性与最大公因数，

这里讲到了求解两个数的最大公因数，是的，就是“欧几里德算法” 其实也就是高中时候学过的 “辗转相除法”。

gcd  

A=BxQ +R；

gcd(a, b) 的性质：

定理：如果a，b是不全为0的任意整数，则gcd(a, b)是a与b的线性组合{ax+by:x,y∈Z}中的最小正元素。

推论1：对于任意整数a，b，如果d|a并且d|b，则d|gcd(a, b)。

推论2：对于所有整数a和b以及任意非负整数n，gcd(an, bn)=n*gcd(a,b)。

推论3：对所有正整数n，a和b，如果n|ab并且gcd(a, n)=1，则n|b。

 

互质数：

如果两个整数a与b只有公因数1，即如果gcd(a, b)=1，则a与b称为互质数。

定理：对任意整数a，b和p，如果gcd(a, p)=1且gcd(b, p)=1，则gcd(ab, p) = 1。

 

GCD递归定理：对任意非负整数a和任意正整数b，gcd(a, b) = gcd(b, a mod b)。

 

给出了求最小公倍数的模版：

#include<stdio.h>
int gcd(int a, int b)  { if(a<b) {int t=a; a=b; b=t;}    return b==0?a:gcd(b,a%b);}
int lcm(int a, int b)  { return a*b/gcd(a,b);}
int main()
{
    int a,b;
    while(scanf("%d %d",&a, &b)!=EOF)
    {
        printf("%d
",lcm(a,b));
    }
    return 0;
}

 

二进制最大公约数算法：（效率更高）

如果a和b都是偶数，那么gcd(a, b) = 2gcd(a/2, b/2)。

如果a是奇数，b是偶数，那么gcd(a, b) = gcd(a, b/2)。

如果a和b都是奇数，那么gcd(a, b) =gcd ((a–b)/2, b)。

 

 

--------------------------------------------------华丽的分割线--------------------------------------------------------------------

本章主要考虑的是最大公因数的问题。最大公因数第一次出现记得是在小学的时候，那时老师要求用短除法（实质就是质因子分解）来解决，但是，到高中貌似是必修三的时候才知道，有“辗转相除法”和“更相减损术”等方法能够更快的求出两个数的最大公因数。其中“辗转相除法”就是本章介绍的“欧几里得算法”，但是当时并没有对其正确性进行证明，而今天才知道它的证明过程。

      对于欧几里得算法，我们知道其计算过程为：

                     

      所以我们可以得到Rn可以整除Rn-1，而由于Rn-1有一个因子是Rn，所以Rn-2也能被Rn整除，如此递推上去，可得Rk都可以被Rn整除，而把a和b看成是R-1和R0(为了分清字母和下标，所以在这里R都用大写，后面的部分都为下标)，因此可以推出Rn是a和b的公因数。

      那么如何判断该数是最大的公因数呢？假设d是a和b的公因数，那么显然有d|a,d|b，对于第一个式子有d|a,d|b，那么显然d|R1，同理，对第二个式子有d|R2，一直递推到最后一个式子，那么有d|Rn，那么对于任意a和b的公因数都能被Rn整除，又因为Rn是a和b的公约数，那么换句话说，Rn就是a和b的最大公约数。至此就证明了Rn是a和b的最大公约数。

      前面提到了高中还学了一种方法叫辗转相除法，那么它的工作方法如下：

              

      原理是这样的:由于Rn-1=Rn-2，所以由倒数第二个式子可得Rn-2可以被Rn整除，倒数第三个式子就可以看出Rn-3能被Rn整除，一直往上推，那么最后就可以证得a和b都能被Rn整除。而证明答案的最大性也与前面证明欧几里得定理的方法类似：假设d|a,d|b，那么d|R0，从上往下推到d|Rn，就可以得出Rn的最大性。

      用欧几里得定理解最大公约数的时候主要问题是涉及除法，取模，开销比较大，用辗转相除法虽然没有除法运算，但是很悲剧如果出现了x远大于y的情况，例如求gcd(10000000,1)，那么需要迭代的次数太多，为了解决这些缺点，《编程之美》中给出了一种方法：

      如果x和y都是偶数，那么x和y同右移一位（除以2），答案乘以2；如果x和y有一个是奇数，那么就让偶数的那个数右移一位，如果x和y都是奇数，那么就将较大的数换成|x-y|，这样得到的 |x-y|是偶数。最后如果x=y，那么再将答案乘上x即可。位运算方法速度较快，可以很好的克服第一个方法的缺点。

      不过对于一般的数据，欧几里得算法还是可以很快出来结果的，因此，直接用欧几里得算法编程得到下面函数，可以做为欧几里得算法的模板：

      int gcd(int x,int y){return y==0?x:gcd(y,x%y);}

习题5.1

gcd(12345,67890)=15,gcd(54321,9876)=3.

习题5.2

上面的函数可以保证如果输入0 0时不会出现死循环。

习题5.3

这题讨论的是欧几里得算法的效率，也就是说讨论在最多几步之内可以求出最大公约数。

推导如下：

          

      因此，最坏情况为每两次计算缩小一半，也就是2^p=t，其中t为Max(x,y)，p为步数k/2。所以有log₂ t=p，将p=k/2代入，得步数k=2log₂ t。假设t有s位，也就是k<2log₂ (10^s ）,得到k<2slog₂ 10<7s，因此可以认为最坏情况大约为位数的7倍。

习题5.4

本题讨论最小公倍数问题。

lcm(x,y)，gcd(x,y)，x，y四者的关系推导如下。

故lcm(8,12)=24,lcm(20,30)=60,lcm(51,68)=204,lcm(23,18)=414,

lcm(301337,307829)=171460753。

假设gcd(x,y)=18,lcm(x,y)=720，存在x，y的多解么？推导如下()

习题5.5

本题讨论关于3n+1问题。

我们可以用计算机来解决有关循环长度的问题，得到L(21)=8,L(13)=10,L(31)=107。另外，我们可以发现，对于前100个数进行试验，最后都是在4,2,1上停下来。

第三题，我们需要证明n=8k+4时L(n)=L(n+1)，证明如下：

                  

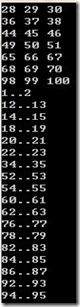
      同理，对n=128k+28时，L(n)=L(n+1)=L(n+2)的证明也可以用上述方法，在此略过。而对于连续的n有相同的L值的情况，打表可以得出如下结果：

            

上图前面三个数一行的表示连续三个数值相同，下面则是相邻两个数值相同。在这些数据中，其中的规律还有待进一步发掘。